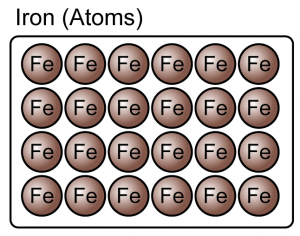
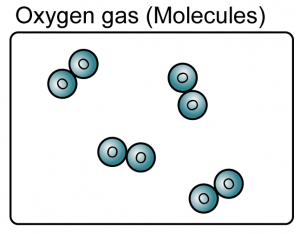
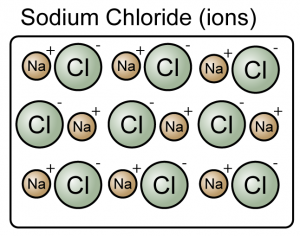
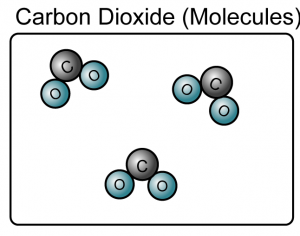
Question 1:
Diagram below is part of a number line.
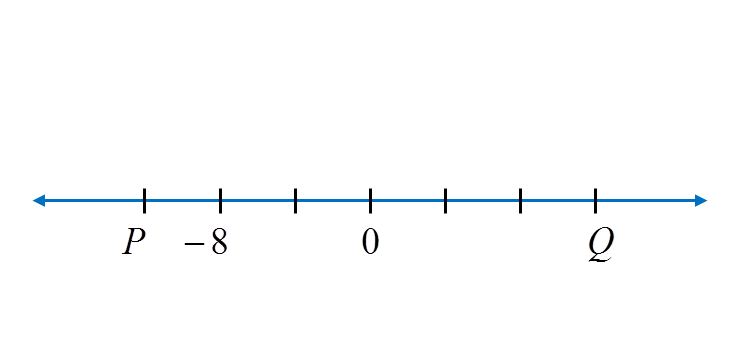 What is the value of P and of Q?
What is the value of P and of Q?
Solution:
Each gradation on the number line represents 4 units. Thus P = –12 and Q = 12.
Diagram below is part of a number line.
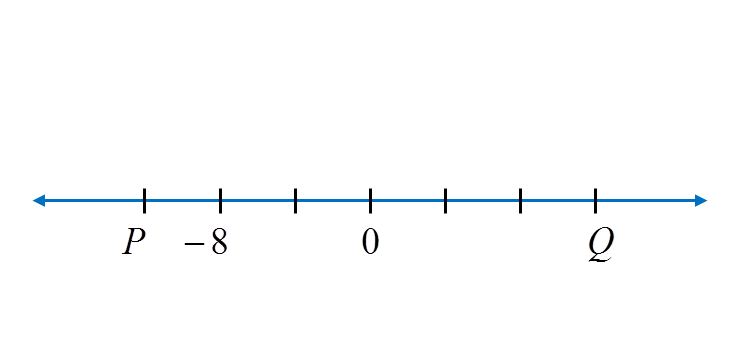 What is the value of P and of Q?
What is the value of P and of Q?Solution:
Each gradation on the number line represents 4 units. Thus P = –12 and Q = 12.
Question 2:
Diagram below shows a sequence of numbers. K and M represent two numbers.
19 13 K 1 M What are the values of K and M?
Solution:
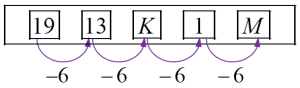
K = 13 – 6 = 7
M = 1 – 6 = –5
Diagram below shows a sequence of numbers. K and M represent two numbers.
19 13 K 1 M What are the values of K and M?
Solution:
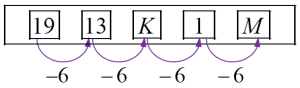
K = 13 – 6 = 7
M = 1 – 6 = –5
Question 3:
Diagram below shows five integers.
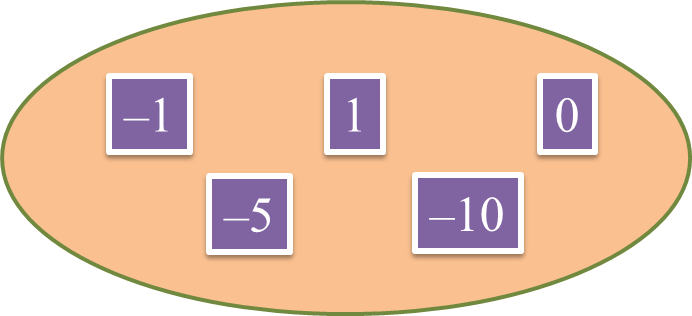
Find the sum of the largest integer and the smallest integer.
Solution:
The largest integer = 1
The smallest integer = –10
Sum of the largest integer and the smallest integer
= 1 + (–10)
= –9
Diagram below shows five integers.

Find the sum of the largest integer and the smallest integer.
Solution:
The largest integer = 1
The smallest integer = –10
Sum of the largest integer and the smallest integer
= 1 + (–10)
= –9