Author: user
8.5.1 Alloy (Structured Questions)
Question 1:
Figure 1.1 shows the formation of bronze.
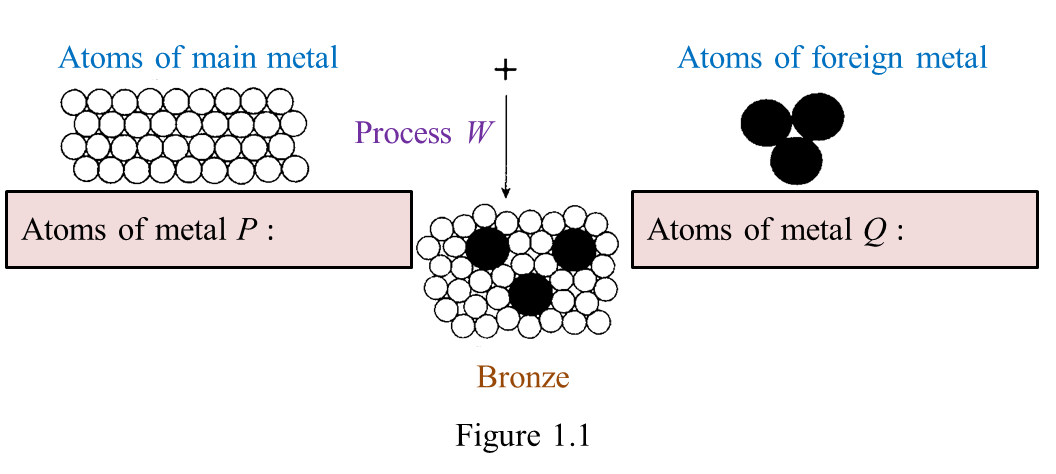
(a) On figure 1.1, name the atoms of metals, P and Q. [2 marks]
(b) Name process W. [1 mark]
(c)(i) State one property of bronze. [1 mark]
(ii) State the effect of the atoms of metal Q in bronze. [1 mark]
 (d) The medal in Figure 1.2 is made of bronze.
(d) The medal in Figure 1.2 is made of bronze.
Give one property of the medal if it is made of metal P only. [1 mark]
Answer:
(a)
P: Copper
Q: Tin
(b)
Alloying
(c)(i) Harder/ can withstand corrosion better than copper.
(c)(ii) The atoms of metal Q in bronze prevent the layers of atoms of metal W in the bronze from sliding easily over one another.
(d) Softer, more malleable, less resistant to corrosion.
Figure 1.1 shows the formation of bronze.

(a) On figure 1.1, name the atoms of metals, P and Q. [2 marks]
(b) Name process W. [1 mark]
(c)(i) State one property of bronze. [1 mark]
(ii) State the effect of the atoms of metal Q in bronze. [1 mark]
 (d) The medal in Figure 1.2 is made of bronze.
(d) The medal in Figure 1.2 is made of bronze.Give one property of the medal if it is made of metal P only. [1 mark]
Answer:
(a)
P: Copper
Q: Tin
(b)
Alloying
(c)(i) Harder/ can withstand corrosion better than copper.
(c)(ii) The atoms of metal Q in bronze prevent the layers of atoms of metal W in the bronze from sliding easily over one another.
(d) Softer, more malleable, less resistant to corrosion.
Question 2:
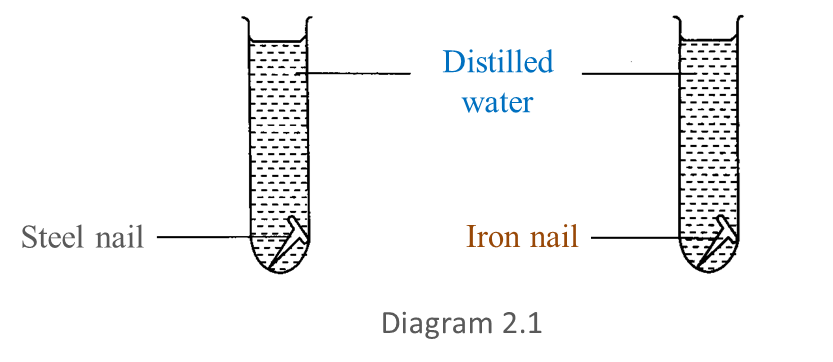
Diagram 2.1 shows an experiment to study the resistance of steel alloy towards corrosion.
After 3 days, the result obtained is shown in Diagram 2.2.
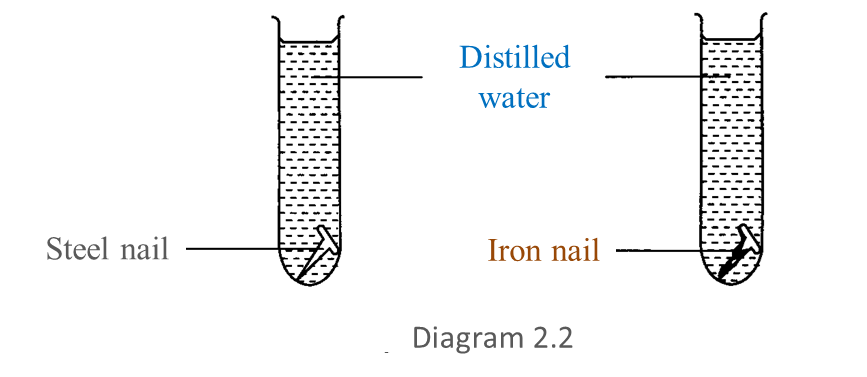
(a) Based on Diagram 2.2, write down one observation for this experiment. [1 mark]
(b) Write down one hypothesis for this experiment. [1 mark]
(c) State the variables in this experiment.
(i) Constant variable [1 mark]
(ii) Manipulated variable [1 mark]
(d) Predict the condition of the steel nail on the 5th day. [1 mark]
(e) Based on this experiment, state the operational definition for an alloy. [1 mark]
Answer:
(a) The iron nail has corroded while the steel nail has not.
(b) Steel is more resistant to corrosion than iron.
(c)(i) Distilled water, number of days the nails are immersed in water.
(any one)
(c)(ii) Type of metal (steel on iron)
(d) The steel nail will remain not corroded
(e) An alloy is a mixture of metal which is harder and more resistant to corrosion than a pure metal.
Diagram 2.1 shows an experiment to study the resistance of steel alloy towards corrosion.

After 3 days, the result obtained is shown in Diagram 2.2.

(a) Based on Diagram 2.2, write down one observation for this experiment. [1 mark]
(b) Write down one hypothesis for this experiment. [1 mark]
(c) State the variables in this experiment.
(i) Constant variable [1 mark]
(ii) Manipulated variable [1 mark]
(d) Predict the condition of the steel nail on the 5th day. [1 mark]
(e) Based on this experiment, state the operational definition for an alloy. [1 mark]
Answer:
(a) The iron nail has corroded while the steel nail has not.
(b) Steel is more resistant to corrosion than iron.
(c)(i) Distilled water, number of days the nails are immersed in water.
(any one)
(c)(ii) Type of metal (steel on iron)
(d) The steel nail will remain not corroded
(e) An alloy is a mixture of metal which is harder and more resistant to corrosion than a pure metal.
SPM Science Forecast Paper
[adinserter block="3"]
[WpProQuiz 1]
8.4.1 Radio Communication (Structured Questions)
Question 1:
Diagram 1.1 shows three types of electronic components used in a radio receiver.
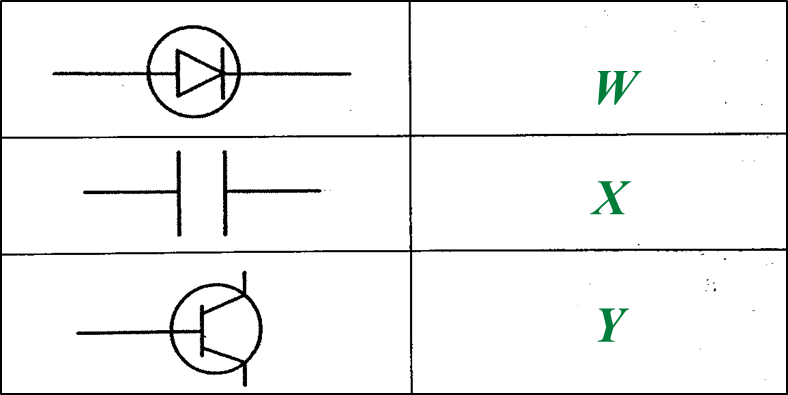 Diagram 1.1
Diagram 1.1
(a) Name electronic components W and Y. [2 marks]
(b) State the function of electronic component X. [1 mark]
(c) Diagram 1.2 shows a black diagram of a radio receiver.
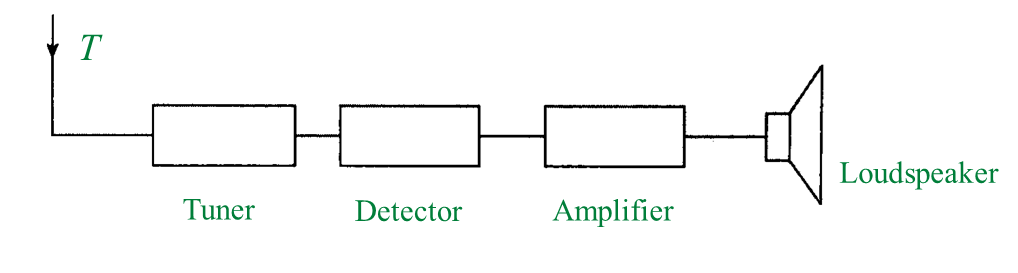 Diagram 1.2
Diagram 1.2
(i) Write any two electronic components, W, X or Y from Diagram 1.1 into the corresponding blocks provided in Diagram 1.2. [2 marks]
(ii) What type of wave is received by T?
Mark (\/) your answer in the box provided in Diagram 1.3. [1 mark]
 Diagram 1.3
Diagram 1.3
Answer:
(a)
W: Diode
Y: Transistor
(b)
(c)(i)
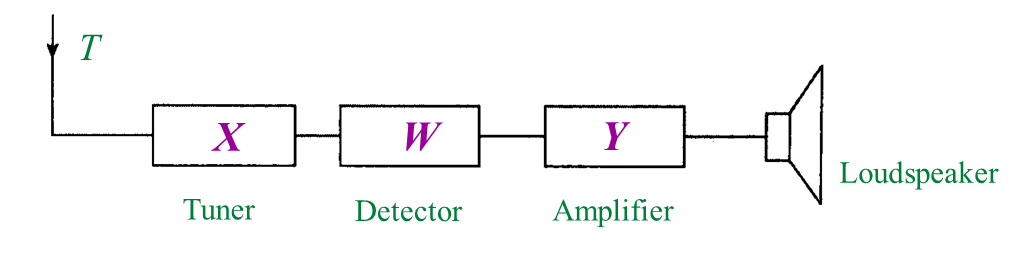 (c)(ii)
(c)(ii)

Diagram 1.1 shows three types of electronic components used in a radio receiver.
 Diagram 1.1
Diagram 1.1(a) Name electronic components W and Y. [2 marks]
(b) State the function of electronic component X. [1 mark]
(c) Diagram 1.2 shows a black diagram of a radio receiver.
 Diagram 1.2
Diagram 1.2(i) Write any two electronic components, W, X or Y from Diagram 1.1 into the corresponding blocks provided in Diagram 1.2. [2 marks]
(ii) What type of wave is received by T?
Mark (\/) your answer in the box provided in Diagram 1.3. [1 mark]
 Diagram 1.3
Diagram 1.3Answer:
(a)
W: Diode
Y: Transistor
(b)
- Stores electric charges and discharges them at regular intervals when required
- To channel the flow of radio frequency carrier waves into the Earth.
- When connected in parallel with the inductor, it determines the frequency of the radio wave that will be detected.
(any one)
(c)(i)
 (c)(ii)
(c)(ii)
Question 2:
Table 1 shows the symbols of electronic components.
(a) Complete Table 1 using the name of electronic components given. [3 marks]
 Table 1
Table 1
Diagram 2 shows a block diagram of a radio receiver system.
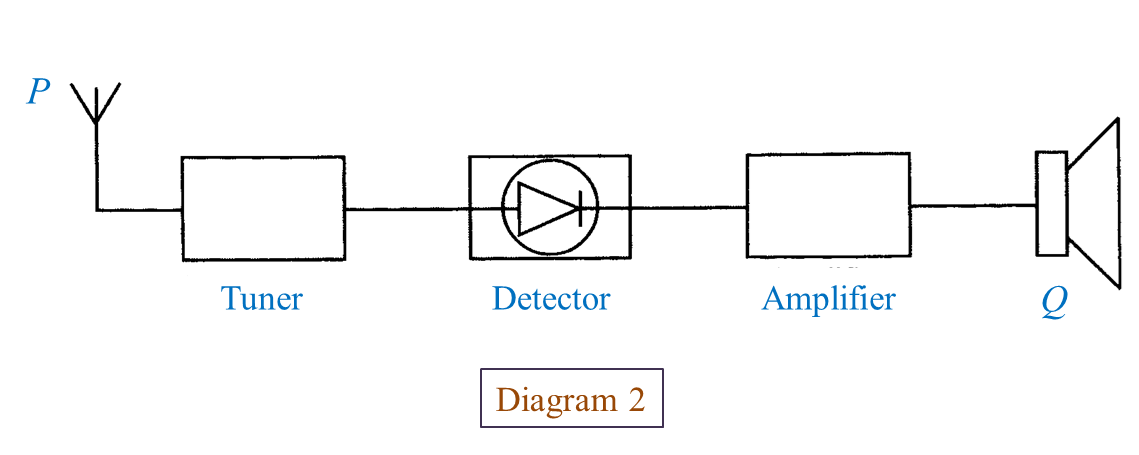 (b) What is the function of P? [1 mark]
(b) What is the function of P? [1 mark]
(c) What is Q? [1 mark]
(d) State the energy change that occurs at Q? [1 mark]
Answer:
(a)
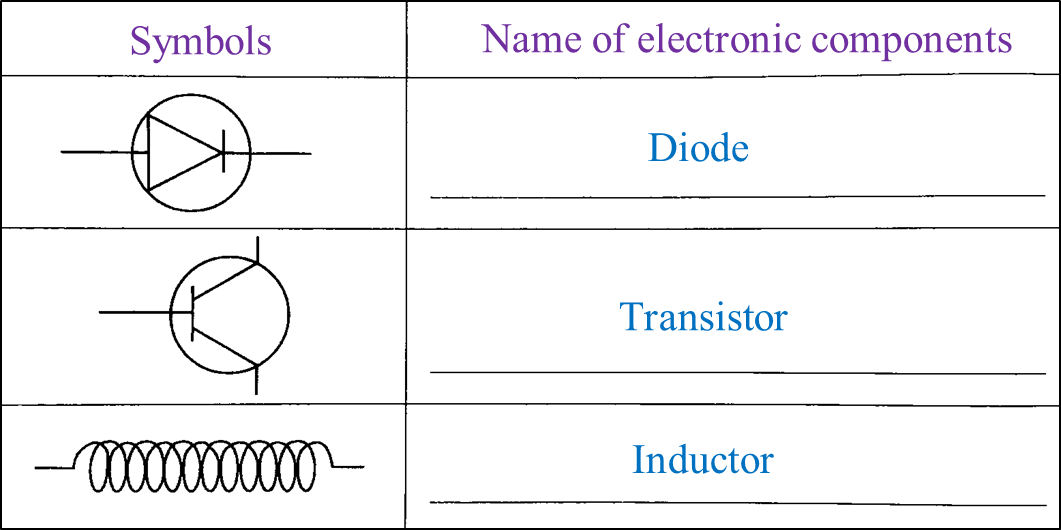
Table 1 shows the symbols of electronic components.
(a) Complete Table 1 using the name of electronic components given. [3 marks]

 Table 1
Table 1Diagram 2 shows a block diagram of a radio receiver system.
 (b) What is the function of P? [1 mark]
(b) What is the function of P? [1 mark](c) What is Q? [1 mark]
(d) State the energy change that occurs at Q? [1 mark]
Answer:
(a)

(b) Receives modulated radio waves from stations.
(c)(i) Loudspeaker
(c)(ii) Electrical energy → sound energy
7.4.3 Practising Responsible Attitudes in the Disposal of Synthetic Polymers (Structured Questions)
Question 1:
Diagram 1 shows containers which are made of synthetic polymer.
 Diagram 1
Diagram 1
(a) Name the type of the synthetic polymer shown in Diagram 1. [1 mark]
(b) State two characteristics of the synthetic polymer in Diagram 1. [2 marks]
(c) What is the effect of improper disposal of the synthetic polymer in Diagram 1 on the environment? [1 mark]
(d) State two correct ways to dispose of the synthetic polymer in Diagram 1 to preserve the environment. [2 marks]
Answer:
(a)
Polythene or polyethene
(b)
- Soft when heated and hard when cooled
- Can be moulded more than once
(c)
Improper disposal of the synthetic polymers such as the burning of synthetic polymers releases toxic gases and acidic gases that cause air pollution and acid rain.
(d)
- Recycle or process again
- Burning in special incinerators which does not release toxic gases into the environment
Diagram 1 shows containers which are made of synthetic polymer.
 Diagram 1
Diagram 1(a) Name the type of the synthetic polymer shown in Diagram 1. [1 mark]
(b) State two characteristics of the synthetic polymer in Diagram 1. [2 marks]
(c) What is the effect of improper disposal of the synthetic polymer in Diagram 1 on the environment? [1 mark]
(d) State two correct ways to dispose of the synthetic polymer in Diagram 1 to preserve the environment. [2 marks]
Answer:
(a)
Polythene or polyethene
(b)
- Soft when heated and hard when cooled
- Can be moulded more than once
(c)
Improper disposal of the synthetic polymers such as the burning of synthetic polymers releases toxic gases and acidic gases that cause air pollution and acid rain.
(d)
- Recycle or process again
- Burning in special incinerators which does not release toxic gases into the environment
7.4.2 Plastics (Structured Questions)
Question 1:
Table 1 shows the characteristics of plastic A and plastic B.
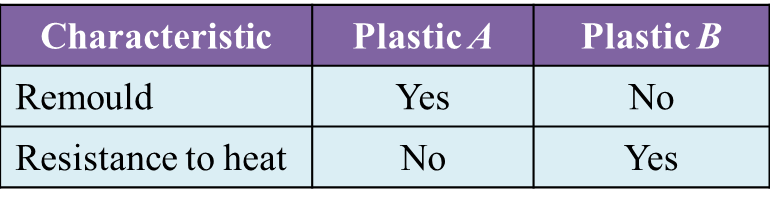 Table 1
Table 1
(a) State the type of plastic A and B. [2 marks]
(b) State one example of plastic A and B. [2 marks]
(c) Which plastic can be recycled? [1 mark]
(d) Which plastic is suitable to make as the handle of an iron? [1 mark]
Answer:
(a)
A: Thermoplastic
B: Thermosetting plastic (Thermoset)
(b)
A: Perspex
B: Bakelite
(c)
Perspex
(d)
Bakelite
Table 1 shows the characteristics of plastic A and plastic B.
 Table 1
Table 1(a) State the type of plastic A and B. [2 marks]
(b) State one example of plastic A and B. [2 marks]
(c) Which plastic can be recycled? [1 mark]
(d) Which plastic is suitable to make as the handle of an iron? [1 mark]
Answer:
(a)
A: Thermoplastic
B: Thermosetting plastic (Thermoset)
(b)
A: Perspex
B: Bakelite
(c)
Perspex
(d)
Bakelite
7.4.1 Synthetic Polymers (Structured Questions)
Question 1:
Table 1.1 shows two types of product made of rubber.
(a) Complete Table 1.1. [4 marks]
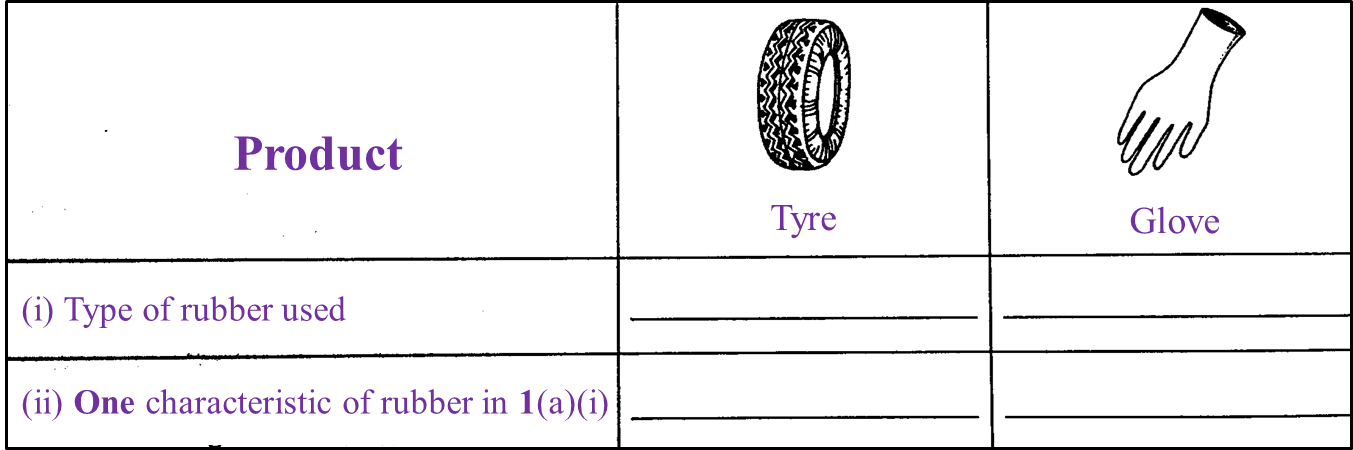 Table 1.1
Table 1.1
[adinserter block="3"]
(b) Table 1.2 shows the characteristics of plastic A and plastic B.
 Table 1.2
Table 1.2
In Table 1.2, state the type of plastic A and plastic B. [2 marks]
[adinserter block="3"]
Answer:
(a)

(b)

Table 1.1 shows two types of product made of rubber.
(a) Complete Table 1.1. [4 marks]
 Table 1.1
Table 1.1[adinserter block="3"]
(b) Table 1.2 shows the characteristics of plastic A and plastic B.
 Table 1.2
Table 1.2In Table 1.2, state the type of plastic A and plastic B. [2 marks]
[adinserter block="3"]
Answer:
(a)

(b)

15.2.3 Trigonometry, PT3 Focus Practice
Question 10:
A technician needs to climb a ladder to repair a street lamp as shown in Diagram below.
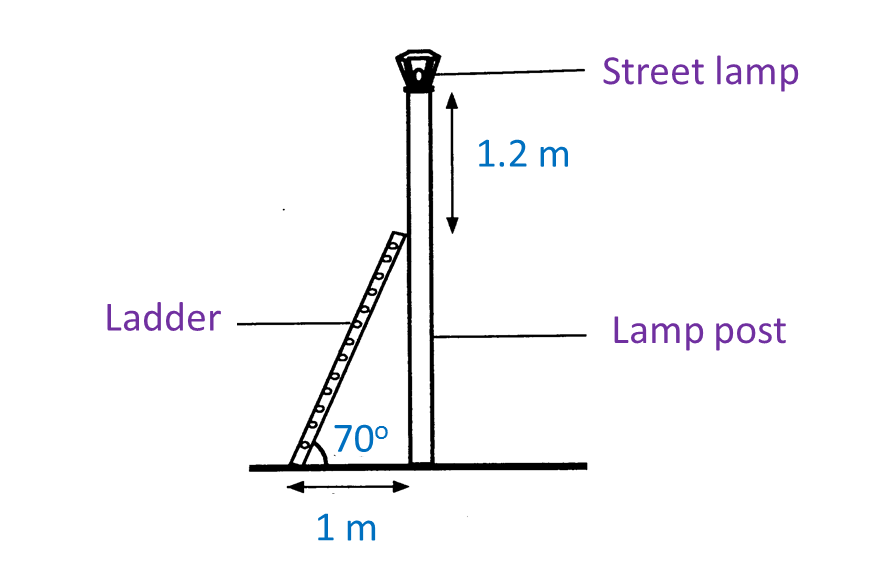 (a) What is the length, in m, of the ladder?
(a) What is the length, in m, of the ladder?
(b) Find the height, in m, of the lamp post.
Solution:

(a)
cos70o=1hh=1cos70oh=10.342h=2.924 mHence, the length of the ladder=2.924 m
(b)
tan70o=T1T=tan70o×1 =2.747×1 =2.747 mThe height of the lamp post=2.747+1.2=3.947 m
A technician needs to climb a ladder to repair a street lamp as shown in Diagram below.
 (a) What is the length, in m, of the ladder?
(a) What is the length, in m, of the ladder?(b) Find the height, in m, of the lamp post.
Solution:

(a)
cos70o=1hh=1cos70oh=10.342h=2.924 mHence, the length of the ladder=2.924 m
(b)
tan70o=T1T=tan70o×1 =2.747×1 =2.747 mThe height of the lamp post=2.747+1.2=3.947 m
15.2.2 Trigonometry, PT3 Focus Practice
Question 6:
In diagram below, AEC and BCD are straight lines. E is the midpoint of AC.
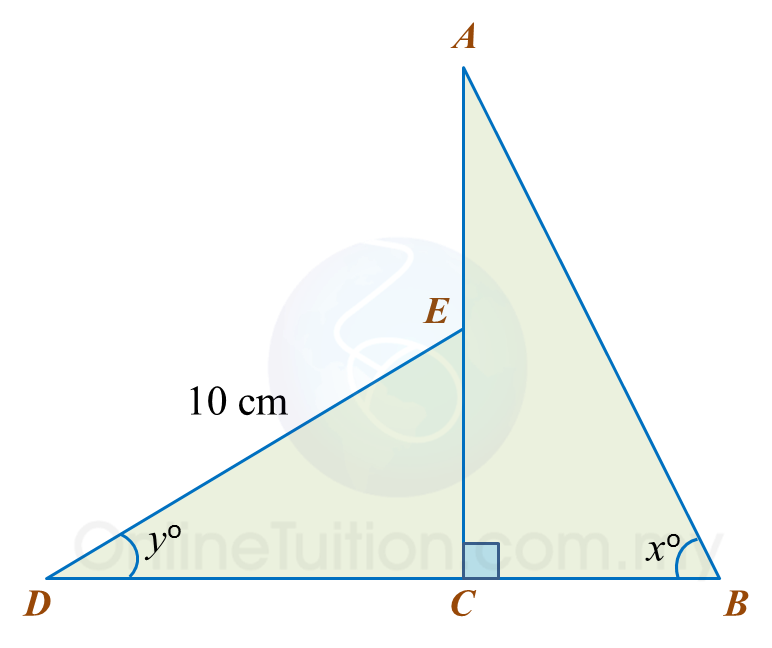
Given cosx=513 and siny=35
(a) find the value of tan x.
(b) Calculate the length, in cm, of BD.
Solution:
(a)Given cos x=513, therefore BC=5, AB=13AC=√132−52 =√169−25 =√144 =12 cmtan x=ACBC=125
(b)For ΔDCE:siny=35ECDE=35EC10=35EC=35×10=6 cmDC2=102−62 =64 DC=8 cmFor ΔABC:AC=2×6=12 cmtanx=12512CB=125CB=5 cmBD=DC+CB=8 cm + 5 cm=13 cm
In diagram below, AEC and BCD are straight lines. E is the midpoint of AC.

Given cosx=513 and siny=35
(a) find the value of tan x.
(b) Calculate the length, in cm, of BD.
Solution:
(a)Given cos x=513, therefore BC=5, AB=13AC=√132−52 =√169−25 =√144 =12 cmtan x=ACBC=125
(b)For ΔDCE:siny=35ECDE=35EC10=35EC=35×10=6 cmDC2=102−62 =64 DC=8 cmFor ΔABC:AC=2×6=12 cmtanx=12512CB=125CB=5 cmBD=DC+CB=8 cm + 5 cm=13 cm
Question 7:
In diagram below, T is the midpoint of the line PR.

(a) Find the value of tan xo.
(b) Calculate the length, in cm, of PQ.
Solution:
(a)TR2=132−122 =169−144 =25TR=√25 =5 cmtanxo=125
(b)PR=2×5 cm =10 cmPQ2=102−82 =100−64 =36PQ=√36 =6 cm
In diagram below, T is the midpoint of the line PR.

(a) Find the value of tan xo.
(b) Calculate the length, in cm, of PQ.
Solution:
(a)TR2=132−122 =169−144 =25TR=√25 =5 cmtanxo=125
(b)PR=2×5 cm =10 cmPQ2=102−82 =100−64 =36PQ=√36 =6 cm
Question 8:
In diagram below, ABE and DBC are two right-angled triangles ABC and DEB are straight lines.
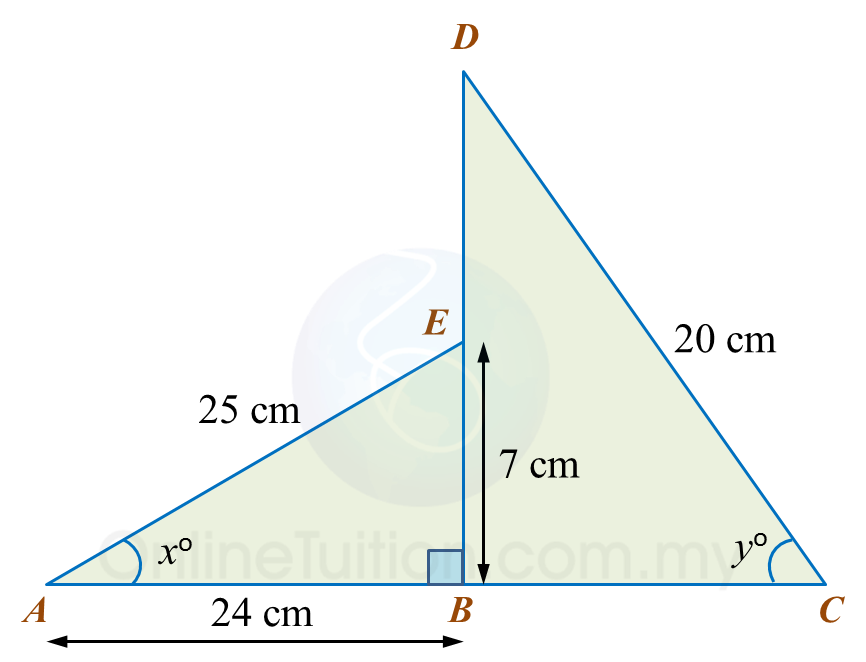
It is given that cosyo=35.
(a) Find the value of tan xo.
(b) Calculate the length, in cm, of DE.
Solution:
(a) tanxo=724
(b)cosyo=BC20 35=BC20BC=35×20 =12 cm∴BD2=202−122 =400−144 =256BD=√256 =16 cmDE=16−7 =9 cm
In diagram below, ABE and DBC are two right-angled triangles ABC and DEB are straight lines.

It is given that cosyo=35.
(a) Find the value of tan xo.
(b) Calculate the length, in cm, of DE.
Solution:
(a) tanxo=724
(b)cosyo=BC20 35=BC20BC=35×20 =12 cm∴BD2=202−122 =400−144 =256BD=√256 =16 cmDE=16−7 =9 cm
Question 9:
Diagram below shows a vertical pole, PQ. At 2.30 p.m. and 5.00 p.m., the shadow of the pole falls on QR and QS respectively.
 Calculate
Calculate
(a) the height, in m, of the pole.
(b) the value of w.
Solution:
(a)
tan 55o=Height of the pole3.2Height of the pole=tan 55o×3.2=1.428×3.2=4.57 m
(b)
tan w=4.573.20+2 =4.575.20 =0.879 w=41o18'
Diagram below shows a vertical pole, PQ. At 2.30 p.m. and 5.00 p.m., the shadow of the pole falls on QR and QS respectively.
 Calculate
Calculate(a) the height, in m, of the pole.
(b) the value of w.
Solution:
(a)
tan 55o=Height of the pole3.2Height of the pole=tan 55o×3.2=1.428×3.2=4.57 m
(b)
tan w=4.573.20+2 =4.575.20 =0.879 w=41o18'
15.2.1 Trigonometry, PT3 Focus Practice
15.2.1 Trigonometry, PT3 Focus Practice
Question 1:
Diagram below shows a right-angled triangle ABC.
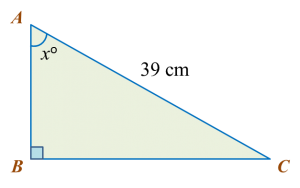
It is given that
cosxo=513
, calculate the length, in cm, of AB.
Solution:
Question 2:
In the diagram, PQR and QTS are straight lines.
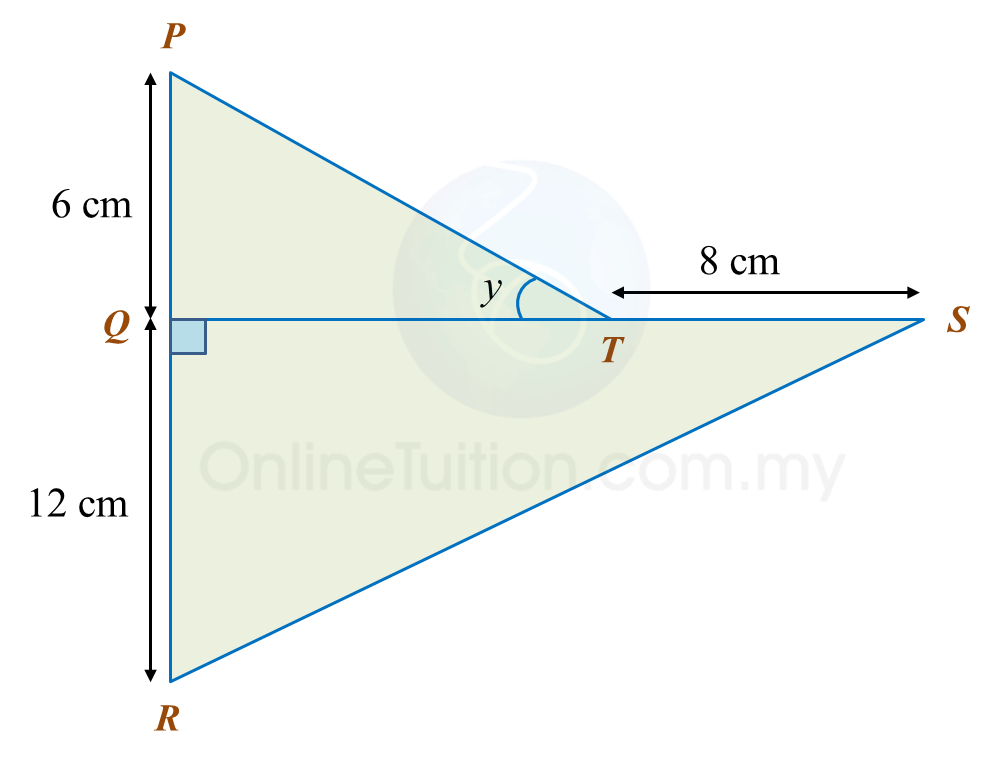

It is given that
tany=34
, calculate the length, in cm, of RS.
Solution:
Question 3:
In the diagram, PQR is a straight line.
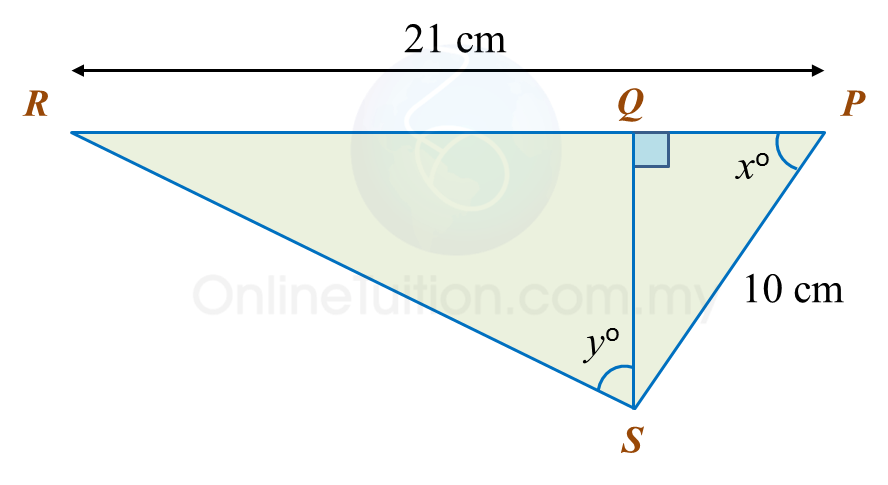
It is given that
cosxo=35
, hence sin yo =
Solution:
cosxo=PQPSPQ10=35PQ=35×10 =6 cmQR=PR−PQ=21−6=15 cm
QS2=102−62← pythagoras' Theorem =100−36 =64QS=√64 =8 cmRS2=152+82 =225+64 =289RS=√289 =17 cmsinyo=1517
Question 4:
Diagram below consists of two right-angled triangles.

Determine the value of cos xo.
Solution:
Question 5:
Diagram below consists of two right-angled triangles ABE and DBC.
ABC and EBD are straight lines.
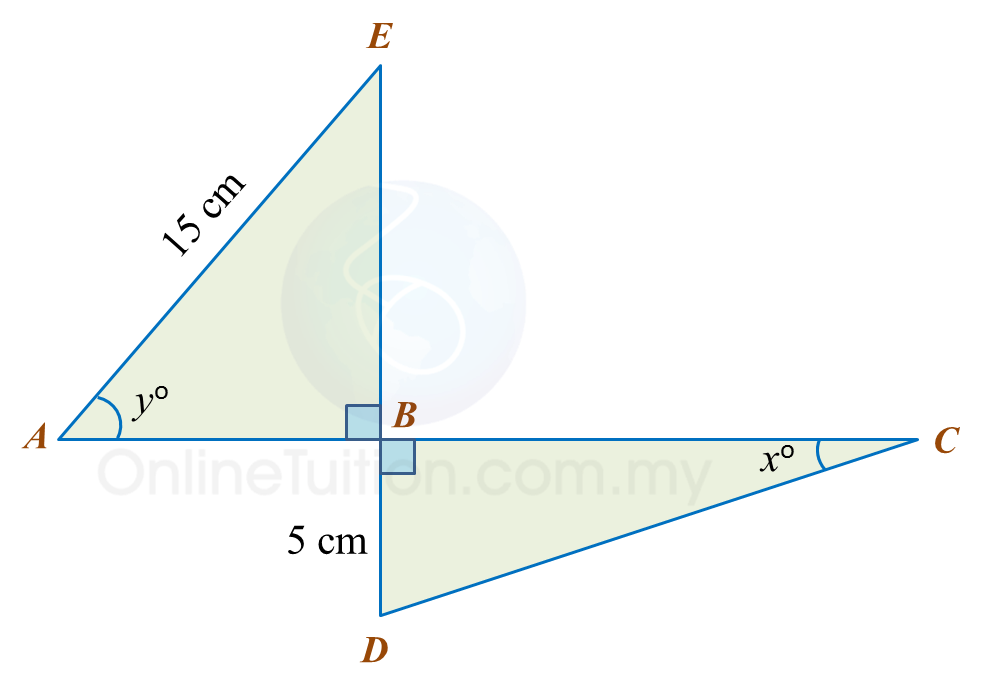

It is given that
sinxo=513 and cosyo=35.
(a) Find the value of tan xo.
(b) Calculate the length, in cm, of ABC.
Solution:
(a)
sinxo=513, DC=13 cmBC=√132−52 =√144 =12 cmThus, tanxo=512
(b)
cosyo=AB15 35=AB15AB=9 cmThus, ABC=9+12 =21 cm