Soalan 9 (6 markah):
Sebuah beg mengandungi lima keping kad berlabel dengan huruf I, J, K, M dan U.
Sekeping kad dipilih secara rawak daripada beg itu dan hurufnya dicatat. Tanpa dikembalikan, sekeping lagi kad dipilih secara rawak daripada beg itu dan hurufnya juga dicatat.
(a) Lengkapkan ruang sampel di ruang jawapan.
(b) Dengan menyenaraikan semua kesudahan peristiwa yang mungkin, cari kebarangkalian bahawa
(i) kad pertama yang dipilih adalah berlabel dengan huruf vokal.
(ii) kad pertama yang dipilih adalah berlabel dengan satu huruf konsonan dan kad kedua yang dipilih adalah berlabel dengan satu huruf vokal.
Jawapan:
{(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , )}
Penyelesaian:
(a)
S = {(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (K, M), (K, U), (M, I), (M, J), (M, K), (M, U), (U, I), (U, J), (U, K), (U, M)}
(b)(i)
{(I, J), (I, K), (I, M), (I, U), (U, I), (U, J), (U, K), (U, M)}
Kebarangkalian kad pertama yang dipilihadalah berlabel dengan huruf vokal=820=25
(b)(ii)
{(J, I), (J, U), (K, I), (K, U), (M, I), (M, U)}
Kebarangkalian=620=310
Sebuah beg mengandungi lima keping kad berlabel dengan huruf I, J, K, M dan U.
Sekeping kad dipilih secara rawak daripada beg itu dan hurufnya dicatat. Tanpa dikembalikan, sekeping lagi kad dipilih secara rawak daripada beg itu dan hurufnya juga dicatat.
(a) Lengkapkan ruang sampel di ruang jawapan.
(b) Dengan menyenaraikan semua kesudahan peristiwa yang mungkin, cari kebarangkalian bahawa
(i) kad pertama yang dipilih adalah berlabel dengan huruf vokal.
(ii) kad pertama yang dipilih adalah berlabel dengan satu huruf konsonan dan kad kedua yang dipilih adalah berlabel dengan satu huruf vokal.
Jawapan:
{(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , )}
Penyelesaian:
(a)
S = {(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (K, M), (K, U), (M, I), (M, J), (M, K), (M, U), (U, I), (U, J), (U, K), (U, M)}
(b)(i)
{(I, J), (I, K), (I, M), (I, U), (U, I), (U, J), (U, K), (U, M)}
Kebarangkalian kad pertama yang dipilihadalah berlabel dengan huruf vokal=820=25
(b)(ii)
{(J, I), (J, U), (K, I), (K, U), (M, I), (M, U)}
Kebarangkalian=620=310
Soalan 10 (6 markah):
Rajah 10.1 menunjukkan satu cakera dengan empat sektor yang sama besar dan satu penunjuk tetap. Setiap satu sektor masing-masing dilabel dengan pemanas air, ketuhar, televisyen dan seterika. Rajah 10.2 menunjukkan sebuah kotak yang mengandungi tiga keping baucer tunai, RM10, RM20 dan RM50.
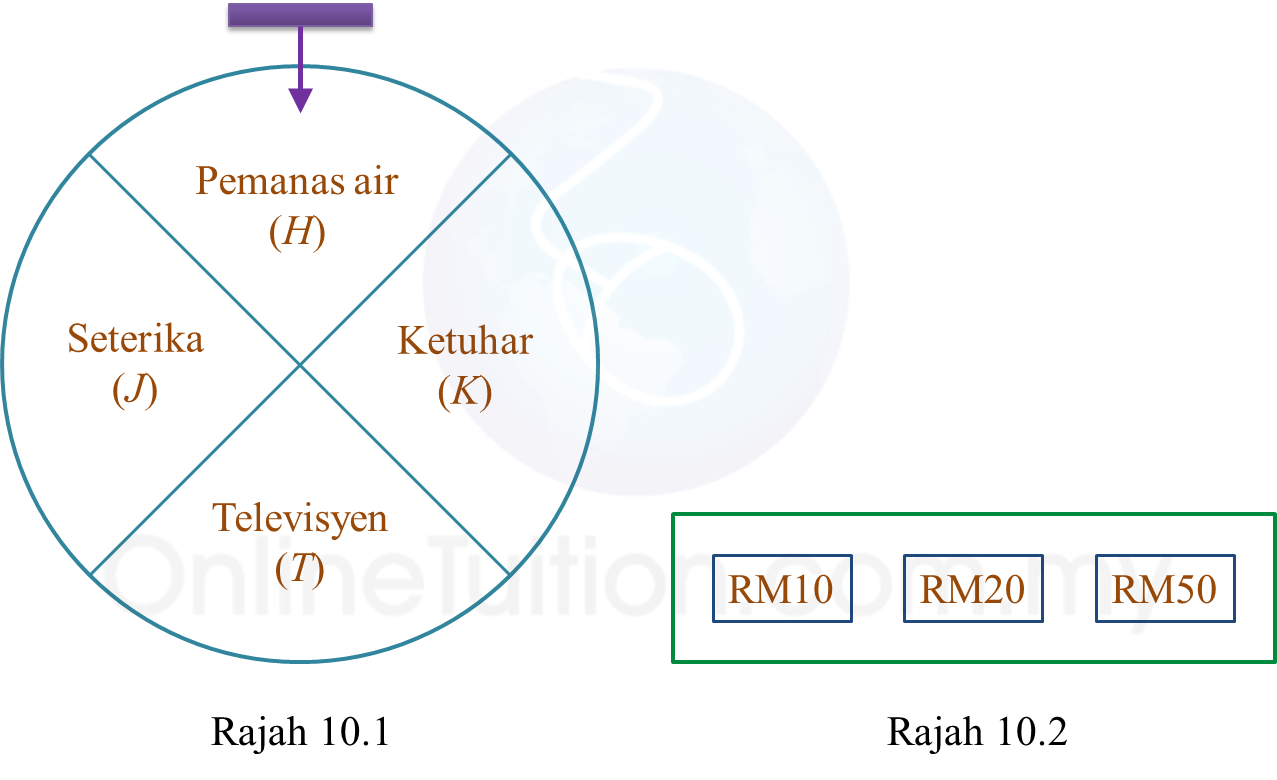
Seorang pelanggan bertuah di sebuah pasar raya diberi peluang untuk memutar cakera sekali dan kemudian membuat satu cabutan baucer tunai daripada kotak itu.
(a) Senaraikan ruang sampel bagi gabungan hadiah yang boleh dimenangi.
(b) Dengan menyenaraikan semua kesudahan yang mungkin bagi peristiwa itu, cari kebarangkalian bahawa
(i) pelanggan itu memenangi sebuah televisyen atau baucer tunai bernilai RM50,
(ii) pelanggan itu tidak memenangi pemanas air dan baucer tunai bernilai RM20.
Penyelesaian:
(a)
S = {(Pemanas air, RM10), (Pemanas air, RM20), (Pemanas air, RM50), (Ketuhar, RM10), (Ketuhar, RM20), (Ketuhar, RM50), (Televisyen, RM10), (Televisyen, RM20), (Televisyen, RM50), (Seterika, RM10), (Seterika, RM20), (Seterika, RM50)}
(b)(i)
{(Pemanas air, RM50), (Ketuhar, RM50), (Seterika, RM50), (Televisyen, RM10), (Televisyen, RM20), (Televisyen, RM50)}
Kebarangkalian=612=12
(b)(ii)
Kebarangkalian=1−P(Pemanas air, RM20)=1−112=1112
Rajah 10.1 menunjukkan satu cakera dengan empat sektor yang sama besar dan satu penunjuk tetap. Setiap satu sektor masing-masing dilabel dengan pemanas air, ketuhar, televisyen dan seterika. Rajah 10.2 menunjukkan sebuah kotak yang mengandungi tiga keping baucer tunai, RM10, RM20 dan RM50.

Seorang pelanggan bertuah di sebuah pasar raya diberi peluang untuk memutar cakera sekali dan kemudian membuat satu cabutan baucer tunai daripada kotak itu.
(a) Senaraikan ruang sampel bagi gabungan hadiah yang boleh dimenangi.
(b) Dengan menyenaraikan semua kesudahan yang mungkin bagi peristiwa itu, cari kebarangkalian bahawa
(i) pelanggan itu memenangi sebuah televisyen atau baucer tunai bernilai RM50,
(ii) pelanggan itu tidak memenangi pemanas air dan baucer tunai bernilai RM20.
Penyelesaian:
(a)
S = {(Pemanas air, RM10), (Pemanas air, RM20), (Pemanas air, RM50), (Ketuhar, RM10), (Ketuhar, RM20), (Ketuhar, RM50), (Televisyen, RM10), (Televisyen, RM20), (Televisyen, RM50), (Seterika, RM10), (Seterika, RM20), (Seterika, RM50)}
(b)(i)
{(Pemanas air, RM50), (Ketuhar, RM50), (Seterika, RM50), (Televisyen, RM10), (Televisyen, RM20), (Televisyen, RM50)}
Kebarangkalian=612=12
(b)(ii)
Kebarangkalian=1−P(Pemanas air, RM20)=1−112=1112




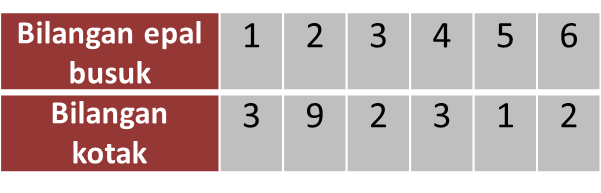 Diberi bahawa terdapat 55 kotak epal. Jika satu kotak dipilih secara rawak, apakah kebarangkalian bahawa kotak itu tidak mengandungi epal busuk?
Diberi bahawa terdapat 55 kotak epal. Jika satu kotak dipilih secara rawak, apakah kebarangkalian bahawa kotak itu tidak mengandungi epal busuk?