Soalan 11 (6 markah):
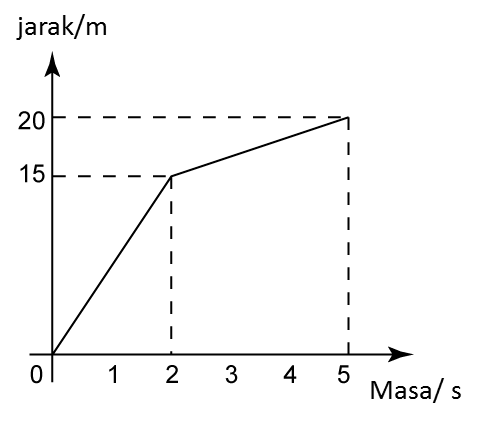
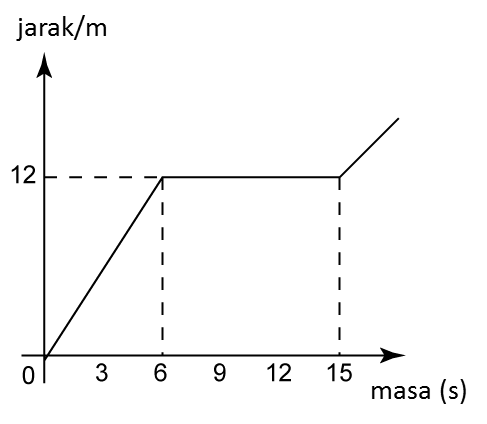
Rajah menunjukkan graf jarak-masa bagi Ursula, Janet dan Maria dalam acara larian 100 m.
 Rajah
Rajah

(a) Siapa yang memenangi perlumbaan itu?
(b) Semasa perlumbaan, Ursula tergelincir dan terjatuh. Selepas itu, dia meneruskan lariannya. Nyatakan tempoh masa, dalam saat, sebelum Ursula meneruskan lariannya.
(c) Semasa perlumbaan, Janet tercedera dan dia berhenti berlari.
Nyatakan jarak Janet, dalam m, dari garisan penamat apabila dia berhenti berlari.
(d) Hitung purata laju, dalam ms-1, bagi Ursula.
Penyelesaian:
(a)
Maria yang memenangi perlumbaan: 100 km dalam 16 saat.
(b)
Tempoh masa sebelum Ursula meneruskan larian daripada tergelincir dan terjatuh
= 18 saat – 9 saat
= 9 saat
(c)
Jarak Janet dari garisan penamat apabila dia berhenti berlari
= 100 m – 70 m
= 30 m
(d)
Purata laju=Jumlah jarakJumlah masa =100 m20 s =5 ms−1Purata laju Ursula=5 ms−1
Rajah menunjukkan graf jarak-masa bagi Ursula, Janet dan Maria dalam acara larian 100 m.
 Rajah
Rajah
(a) Siapa yang memenangi perlumbaan itu?
(b) Semasa perlumbaan, Ursula tergelincir dan terjatuh. Selepas itu, dia meneruskan lariannya. Nyatakan tempoh masa, dalam saat, sebelum Ursula meneruskan lariannya.
(c) Semasa perlumbaan, Janet tercedera dan dia berhenti berlari.
Nyatakan jarak Janet, dalam m, dari garisan penamat apabila dia berhenti berlari.
(d) Hitung purata laju, dalam ms-1, bagi Ursula.
Penyelesaian:
(a)
Maria yang memenangi perlumbaan: 100 km dalam 16 saat.
(b)
Tempoh masa sebelum Ursula meneruskan larian daripada tergelincir dan terjatuh
= 18 saat – 9 saat
= 9 saat
(c)
Jarak Janet dari garisan penamat apabila dia berhenti berlari
= 100 m – 70 m
= 30 m
(d)
Purata laju=Jumlah jarakJumlah masa =100 m20 s =5 ms−1Purata laju Ursula=5 ms−1
Soalan 12 (6 markah):
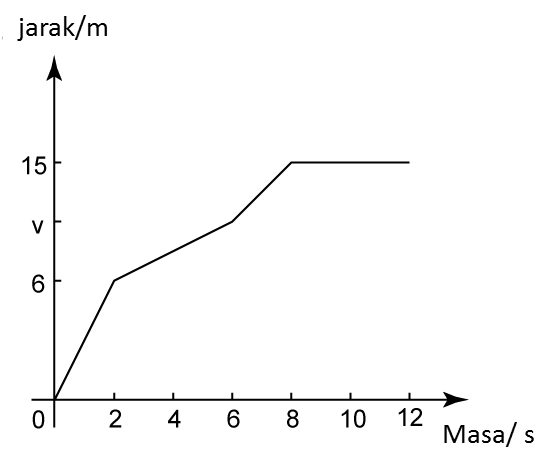
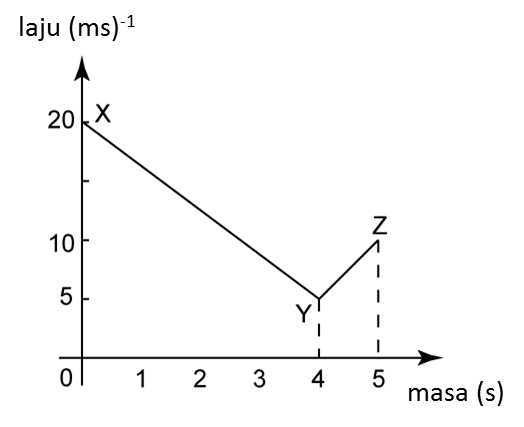
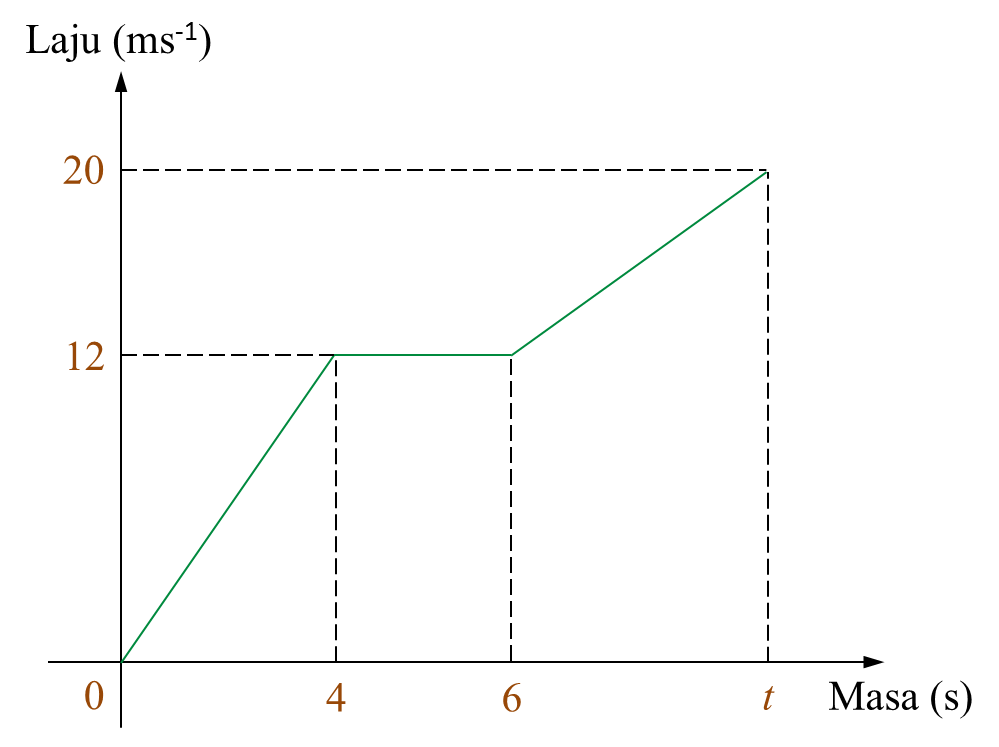
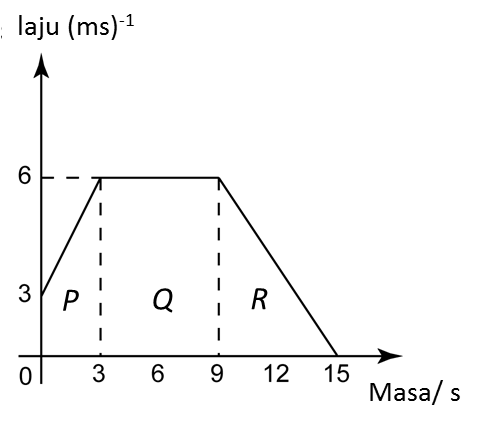
Rajah menunjukkan graf laju-masa bagi pergerakan suatu zarah dalam tempoh t saat.
 Rajah
Rajah
(a) Nyatakan laju seragam, dalam ms-1, zarah itu.
(b) Hitung kadar perubahan laju, dalam ms-2, zarah itu dalam tempoh 4 saat pertama.
(c) Hitung nilai t, jika jarak yang dilalui dalam tempoh 4 saat pertama ialah separuh daripada jarak yang dilalui daripada saat ke-6 hingga saat ke-t.
Penyelesaian:
(a)
Laju seragam zarah = 12 ms-1
(b)
Kadar perubahan laju zarah=124=3 ms−2
(c)
Jarak yang dilalui dalam tempoh 4 saat pertama=12(Jarak yang dilalui daripada saat ke-6 hingga saat ke-t)12×4×12=12[12(12+20)(t−6)]24=12[16(t−6)]24=8(t−6)24=8t−483=t−6t=9
Rajah menunjukkan graf laju-masa bagi pergerakan suatu zarah dalam tempoh t saat.
 Rajah
Rajah(a) Nyatakan laju seragam, dalam ms-1, zarah itu.
(b) Hitung kadar perubahan laju, dalam ms-2, zarah itu dalam tempoh 4 saat pertama.
(c) Hitung nilai t, jika jarak yang dilalui dalam tempoh 4 saat pertama ialah separuh daripada jarak yang dilalui daripada saat ke-6 hingga saat ke-t.
Penyelesaian:
(a)
Laju seragam zarah = 12 ms-1
(b)
Kadar perubahan laju zarah=124=3 ms−2
(c)
Jarak yang dilalui dalam tempoh 4 saat pertama=12(Jarak yang dilalui daripada saat ke-6 hingga saat ke-t)12×4×12=12[12(12+20)(t−6)]24=12[16(t−6)]24=8(t−6)24=8t−483=t−6t=9
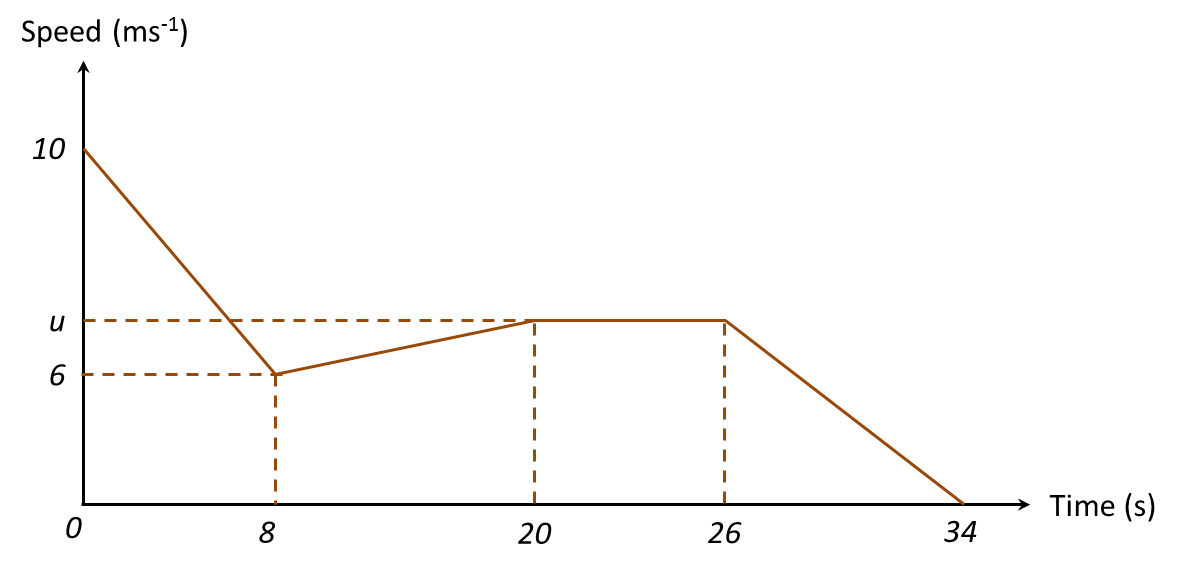 (a) Nyatakan tempoh masa, dalam saat, objek itu bergerak dengan laju seragam.
(a) Nyatakan tempoh masa, dalam saat, objek itu bergerak dengan laju seragam.
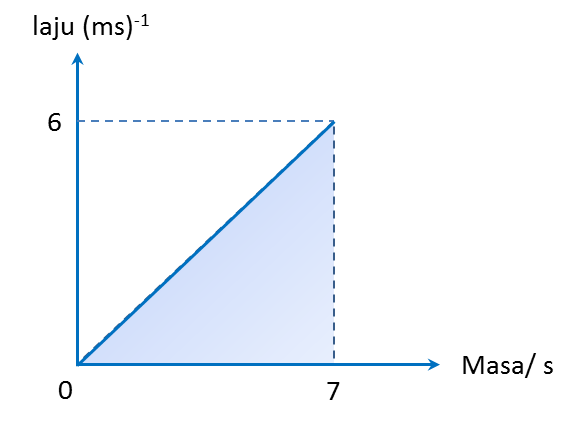
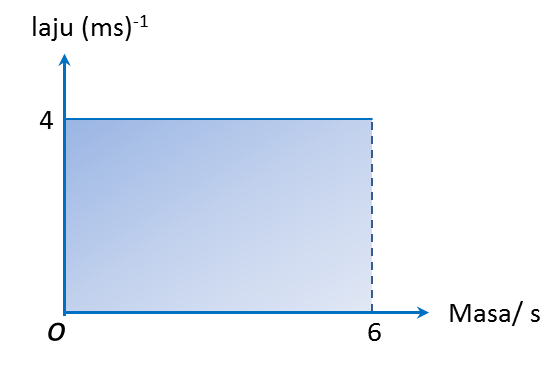
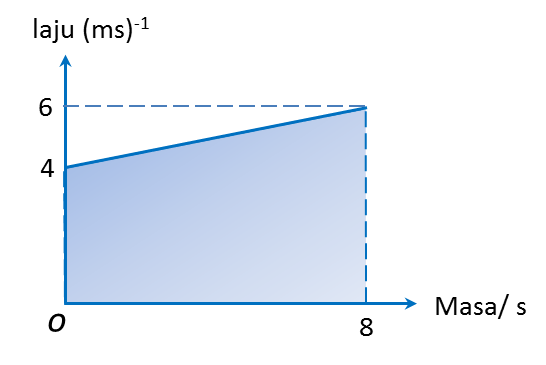
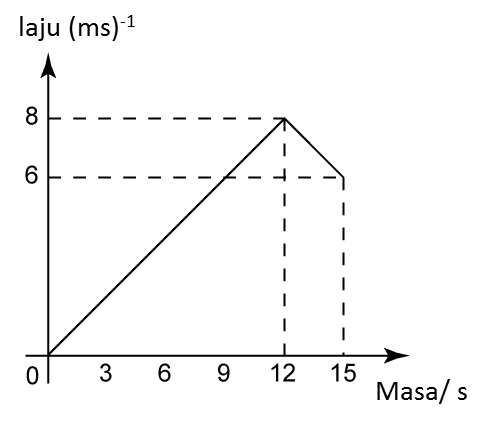
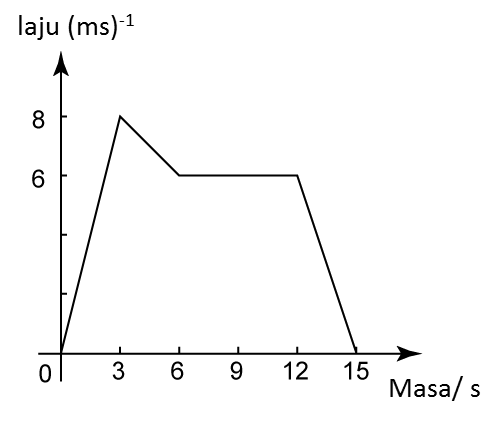


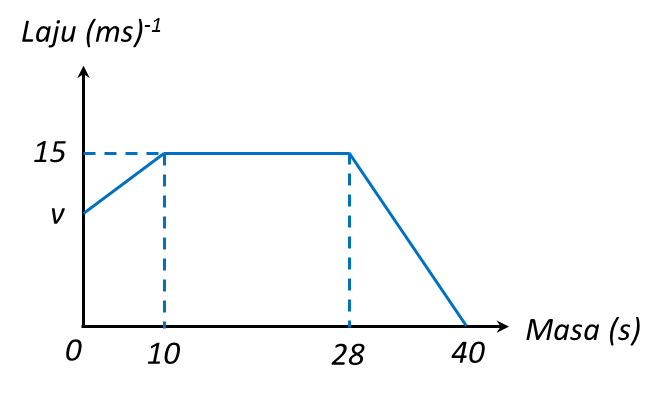 (a) Nyatakan tempoh masa, dalam s, objek itu bergerak dengan laju seragam.
(a) Nyatakan tempoh masa, dalam s, objek itu bergerak dengan laju seragam.