Soalan 9 (12 markah):
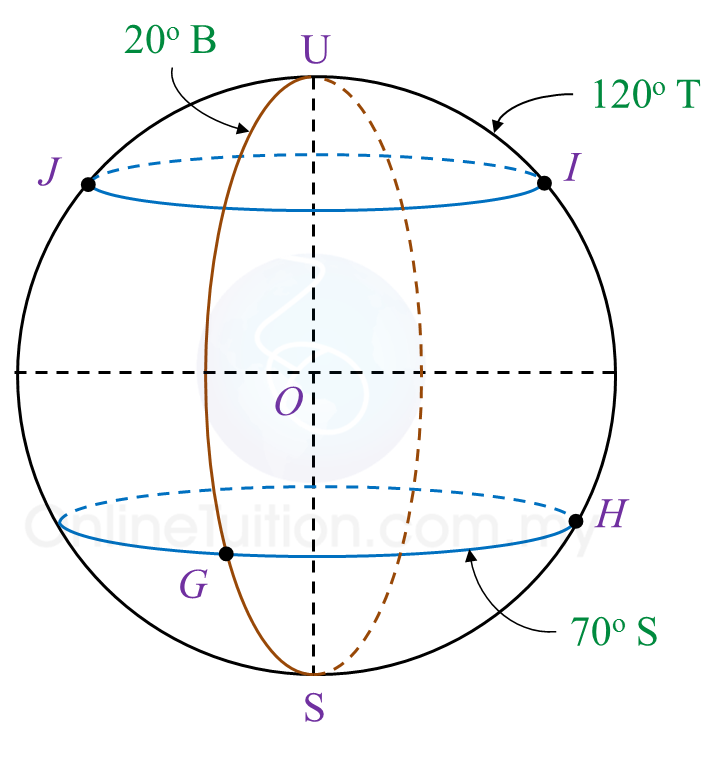
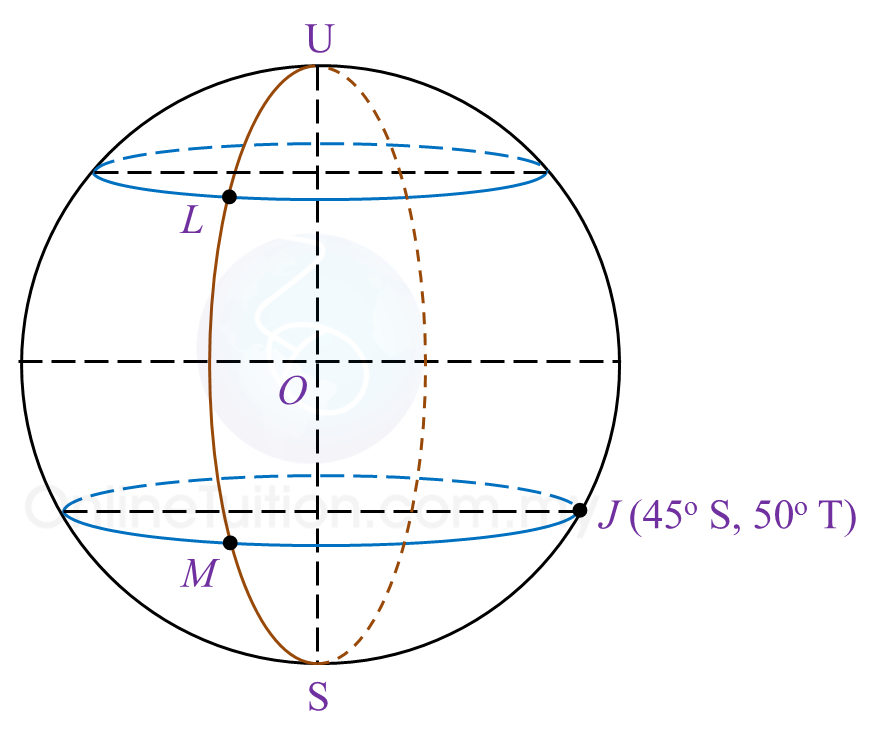
A(25o U, 35o T), B(25o U, 40o B), C dan D adalah empat titik yang terletak pada permukaan bumi. AD ialah diameter selarian latitud sepunya 25o U .
(a) Cari longitud D.
(b) C terletak 3300 batu nautika di selatan A diukur sepanjang permukaan bumi.
Hitung latitud C.
(c) Hitung jarak terpendek, dalam batu nautika, dari A ke D diukur sepanjang permukaan bumi.
(d) Sebuah kapal terbang berlepas dari C dan terbang arah utara ke titik A dan kemudian terbang arah barat ke titik B. Jumlah masa diambil bagi keseluruhan penerbangan itu ialah 12 jam 24 minit.
(i) Hitung jarak, dalam batu nautika, dari A arah barat ke B diukur sepanjang selarian latitud sepunya.
(ii) Hitung purata laju, dalam knot, bagi keseluruhan penerbangan itu.
Penyelesaian:
(a)
Longitud D = (180o – 35o)B
= 145oB
(b)
∠AOC=330060=55oLatitud bagi C=(55−25)oS=30oS
(c)
Jarak terpendek dari A ke D
= (65o + 65o) × 60’
= 130o × 60’
= 7800 batu nautika
[adinserter block="3"]
(d)(i)
Jarak A ke B
= (35o + 40o) × 60’ × kos 25o
= 75o × 60’ × kos 25o
= 4078.4 batu nautika
(d)(ii)
Jumlah jarak dilalui=CA+AB=3300+4078.4=7378.4 batu nautikaPurata laju=Jumlah jarakJumlah masa=7378.412.4 knot=595.0 knot
A(25o U, 35o T), B(25o U, 40o B), C dan D adalah empat titik yang terletak pada permukaan bumi. AD ialah diameter selarian latitud sepunya 25o U .
(a) Cari longitud D.
(b) C terletak 3300 batu nautika di selatan A diukur sepanjang permukaan bumi.
Hitung latitud C.
(c) Hitung jarak terpendek, dalam batu nautika, dari A ke D diukur sepanjang permukaan bumi.
(d) Sebuah kapal terbang berlepas dari C dan terbang arah utara ke titik A dan kemudian terbang arah barat ke titik B. Jumlah masa diambil bagi keseluruhan penerbangan itu ialah 12 jam 24 minit.
(i) Hitung jarak, dalam batu nautika, dari A arah barat ke B diukur sepanjang selarian latitud sepunya.
(ii) Hitung purata laju, dalam knot, bagi keseluruhan penerbangan itu.
Penyelesaian:
(a)
Longitud D = (180o – 35o)B
= 145oB
(b)
∠AOC=330060=55oLatitud bagi C=(55−25)oS=30oS
(c)
Jarak terpendek dari A ke D
= (65o + 65o) × 60’
= 130o × 60’
= 7800 batu nautika
[adinserter block="3"]
(d)(i)
Jarak A ke B
= (35o + 40o) × 60’ × kos 25o
= 75o × 60’ × kos 25o
= 4078.4 batu nautika
(d)(ii)
Jumlah jarak dilalui=CA+AB=3300+4078.4=7378.4 batu nautikaPurata laju=Jumlah jarakJumlah masa=7378.412.4 knot=595.0 knot

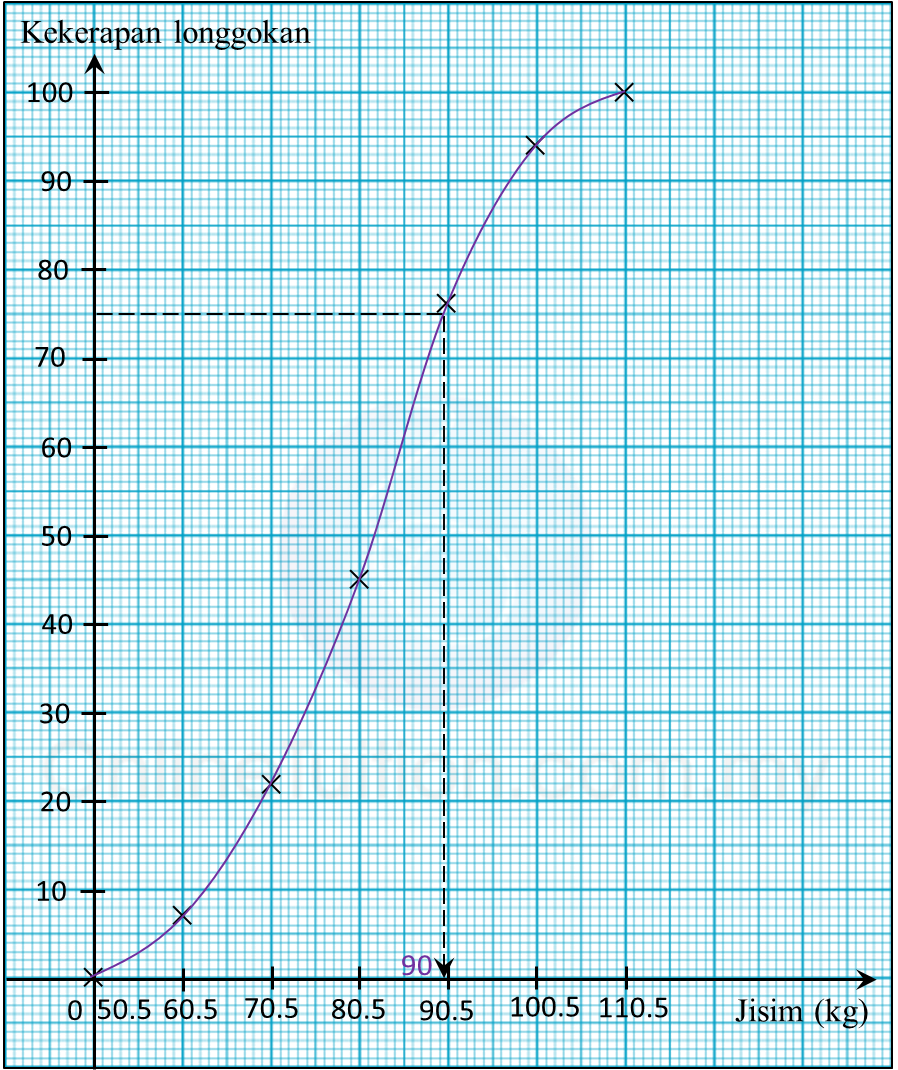
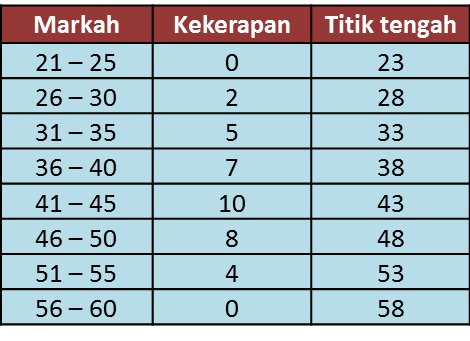
 Rajah 10
Rajah 10


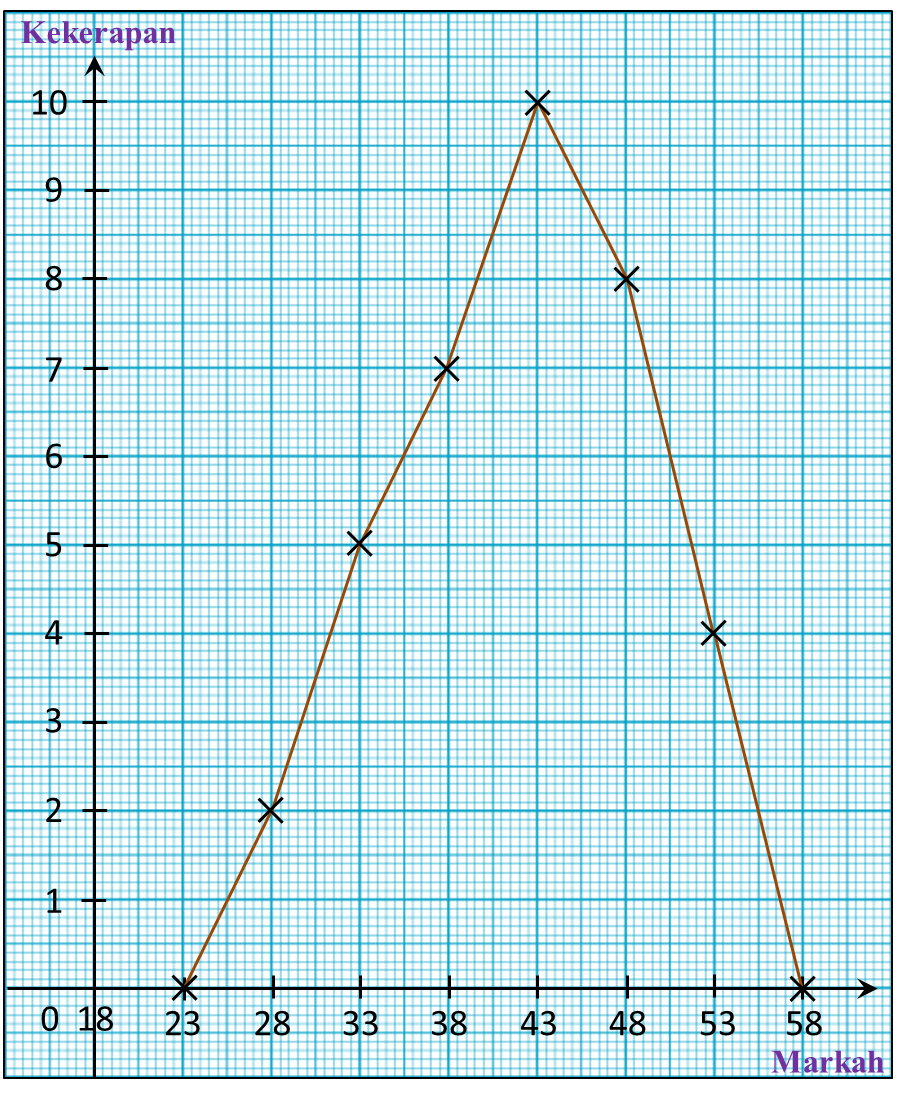
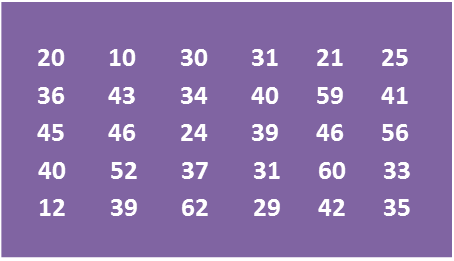 Rajah 9
Rajah 9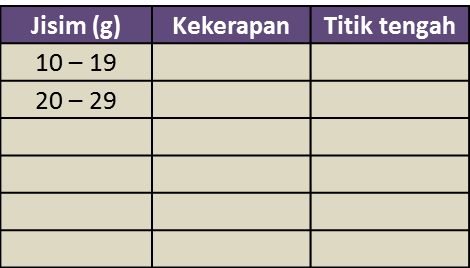
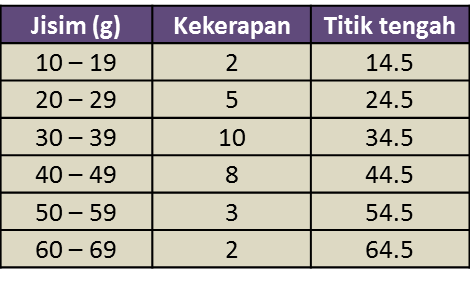
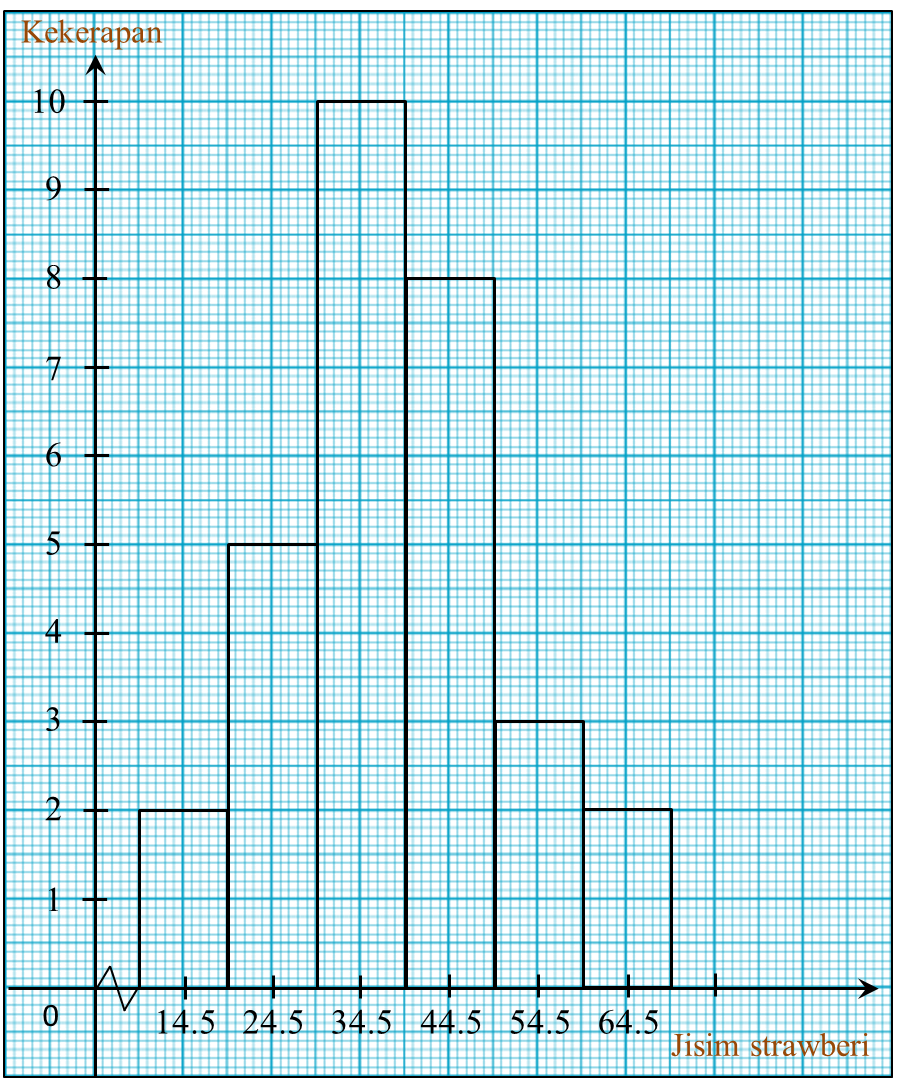
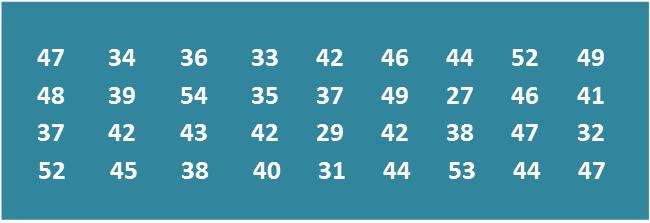
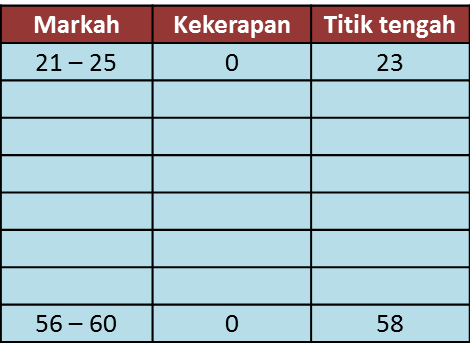
 Rajah 8.1
Rajah 8.1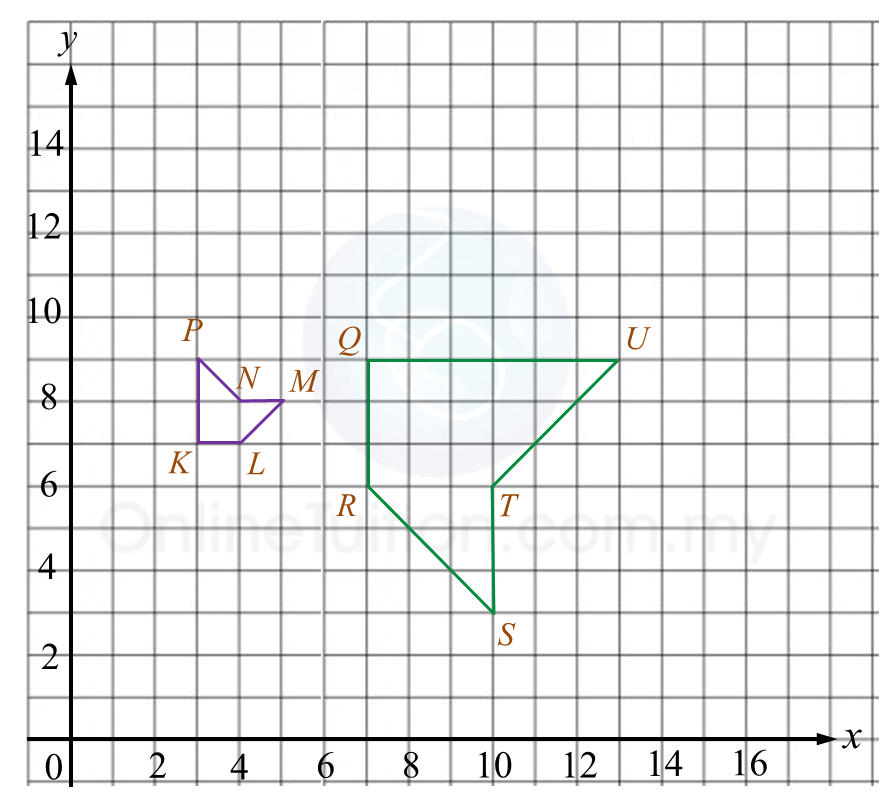 Rajah 10.2
Rajah 10.2
 Rajah 7.1
Rajah 7.1 Rajah 7.2
Rajah 7.2