Soalan 12 (12 markah):
(a) Lengkapkan Jadual 2 di ruang jawapan, bagi persamaan y=30x dengan menulis nilai-nilai y apabila x = 2 dan x = 5.
(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
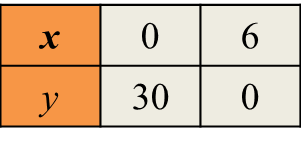
Menggunakan skala 2 cm kepada 1 unit pada paksi-x dan 2 cm kepada 5 unit pada paksi-y, lukis graf y=30x untuk 0≤x≤7.
(c) Daripada graf di 12(b), cari
(i) nilai y apabila x = 2.6,
(ii) nilai x apabila y = 17.5.
(d) Lukis satu garis lurus yang sesuai pada graf di 12(b) untuk mencari nilai-nilai x yang memuaskan persamaan 30x=−5x+30 untuk 0≤x≤7.
Nyatakan nilai-nilai x ini.
Jawapan:

Penyelesaian:
(a)
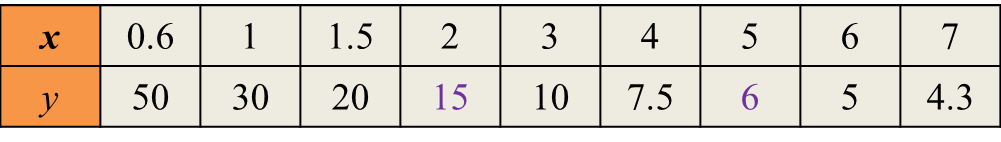
(b)
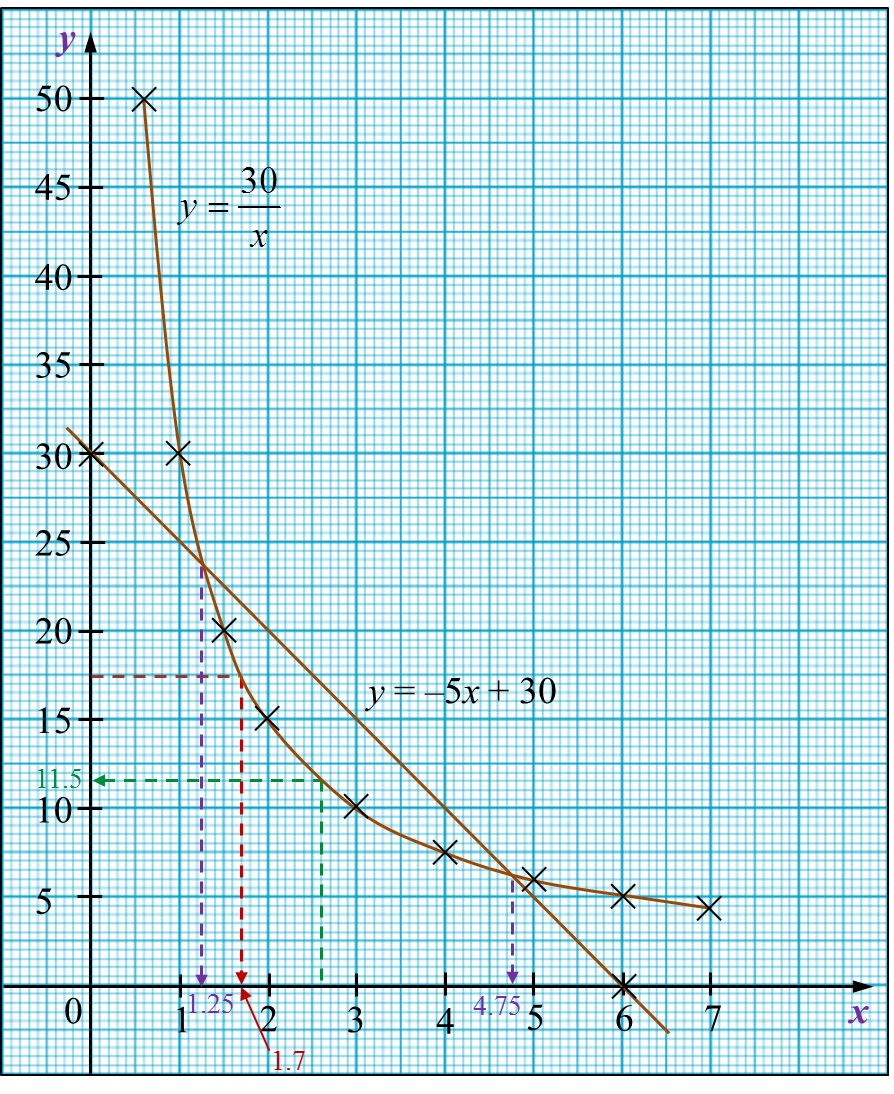
(c) Dari graf
(i) Apabila x = 2.6; y = 11.5
(ii) Apabila y = 17.5; x = 1.7
(d)
Diberi,30x=−5x+30 y=−5x+30Dari graf; x=1.25 dan 4.75
(a) Lengkapkan Jadual 2 di ruang jawapan, bagi persamaan y=30x dengan menulis nilai-nilai y apabila x = 2 dan x = 5.
(b) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Menggunakan skala 2 cm kepada 1 unit pada paksi-x dan 2 cm kepada 5 unit pada paksi-y, lukis graf y=30x untuk 0≤x≤7.
(c) Daripada graf di 12(b), cari
(i) nilai y apabila x = 2.6,
(ii) nilai x apabila y = 17.5.
(d) Lukis satu garis lurus yang sesuai pada graf di 12(b) untuk mencari nilai-nilai x yang memuaskan persamaan 30x=−5x+30 untuk 0≤x≤7.
Nyatakan nilai-nilai x ini.
Jawapan:

Penyelesaian:
(a)
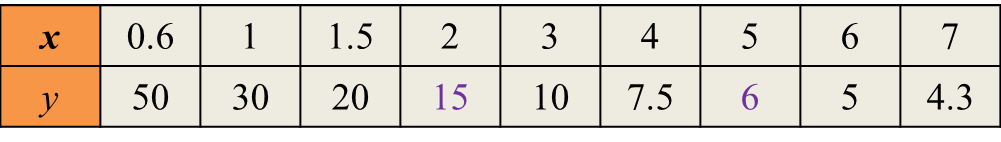
(b)

(c) Dari graf
(i) Apabila x = 2.6; y = 11.5
(ii) Apabila y = 17.5; x = 1.7
(d)
Diberi,30x=−5x+30 y=−5x+30Dari graf; x=1.25 dan 4.75

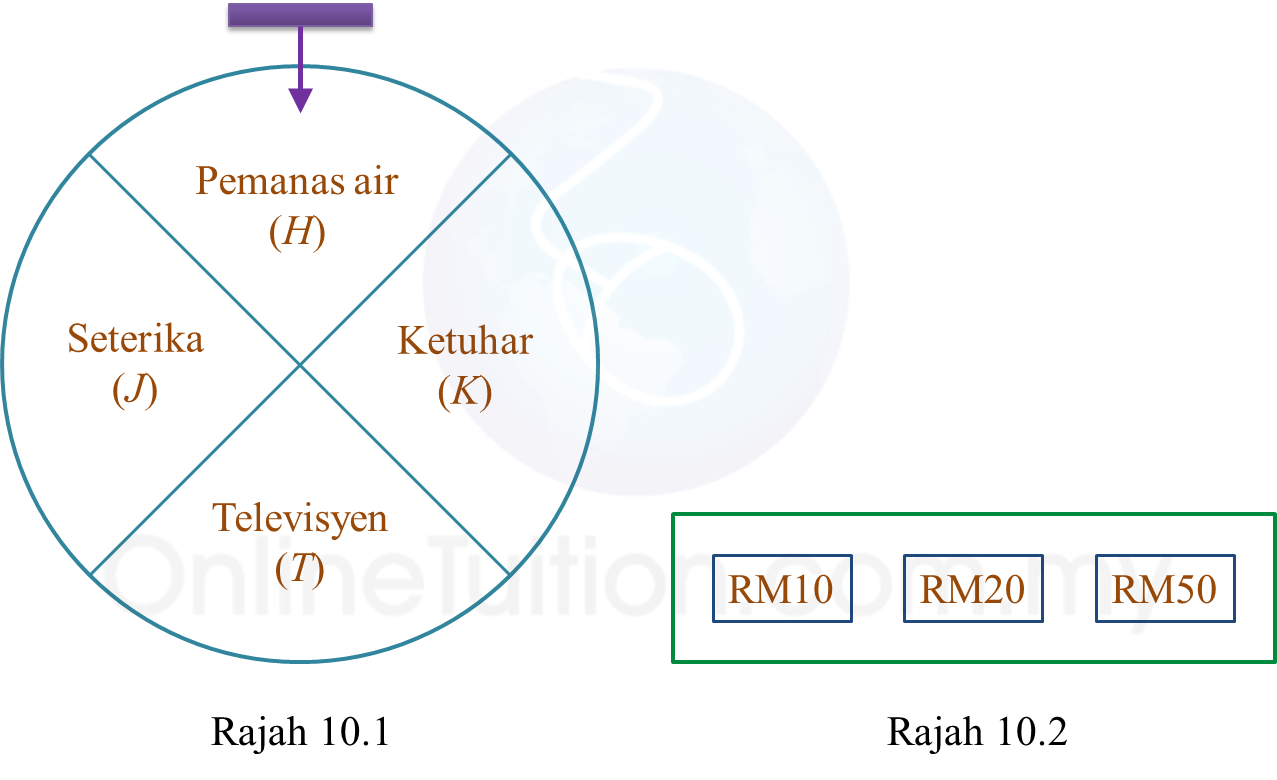
 Rajah
Rajah
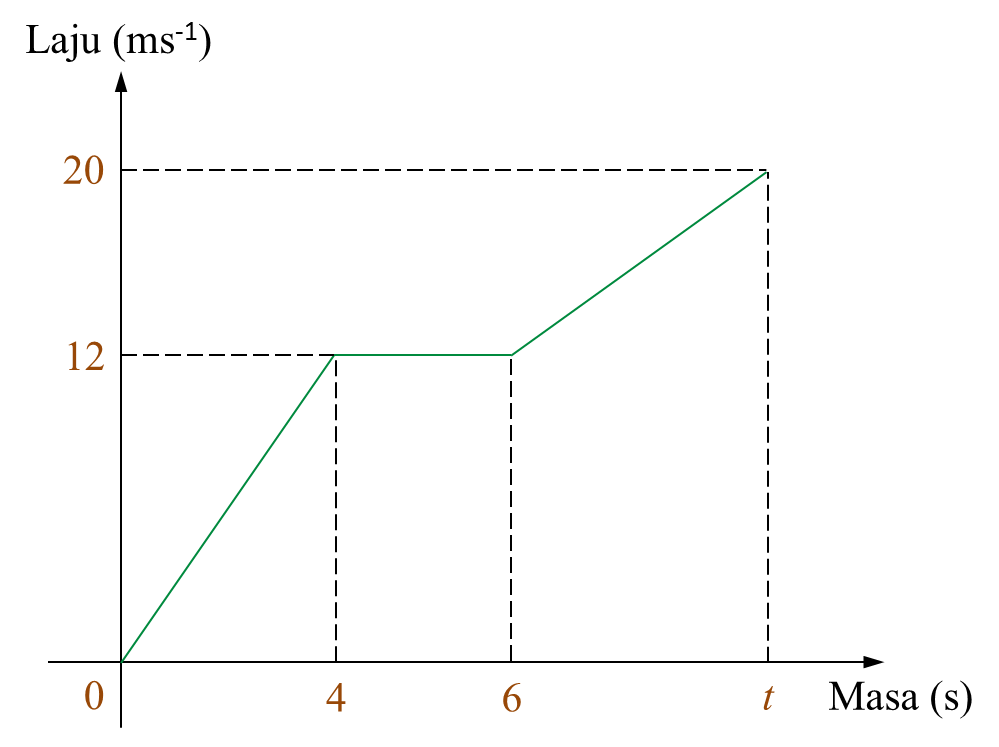 Rajah
Rajah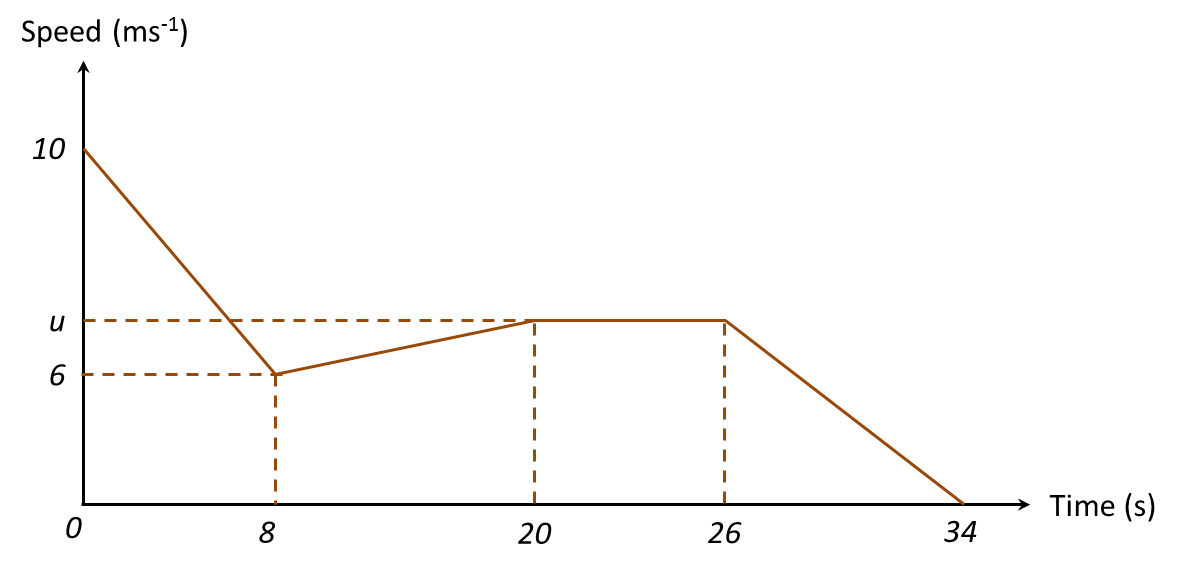 (a) Nyatakan tempoh masa, dalam saat, objek itu bergerak dengan laju seragam.
(a) Nyatakan tempoh masa, dalam saat, objek itu bergerak dengan laju seragam.
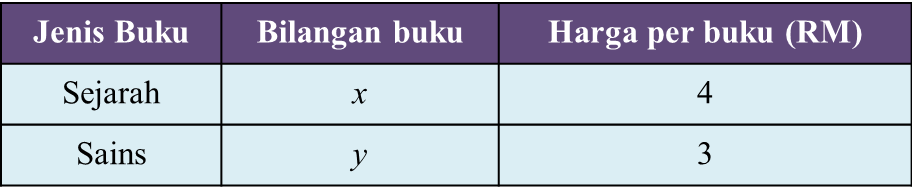 Jadual
Jadual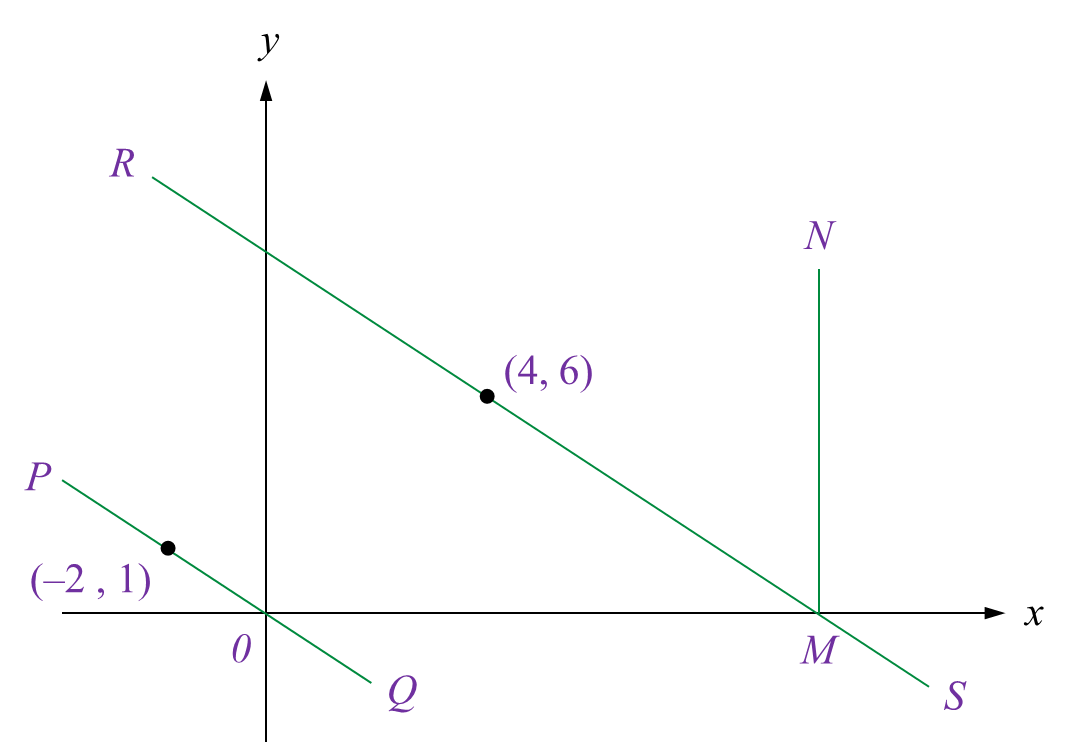 Rajah
Rajah Rajah
Rajah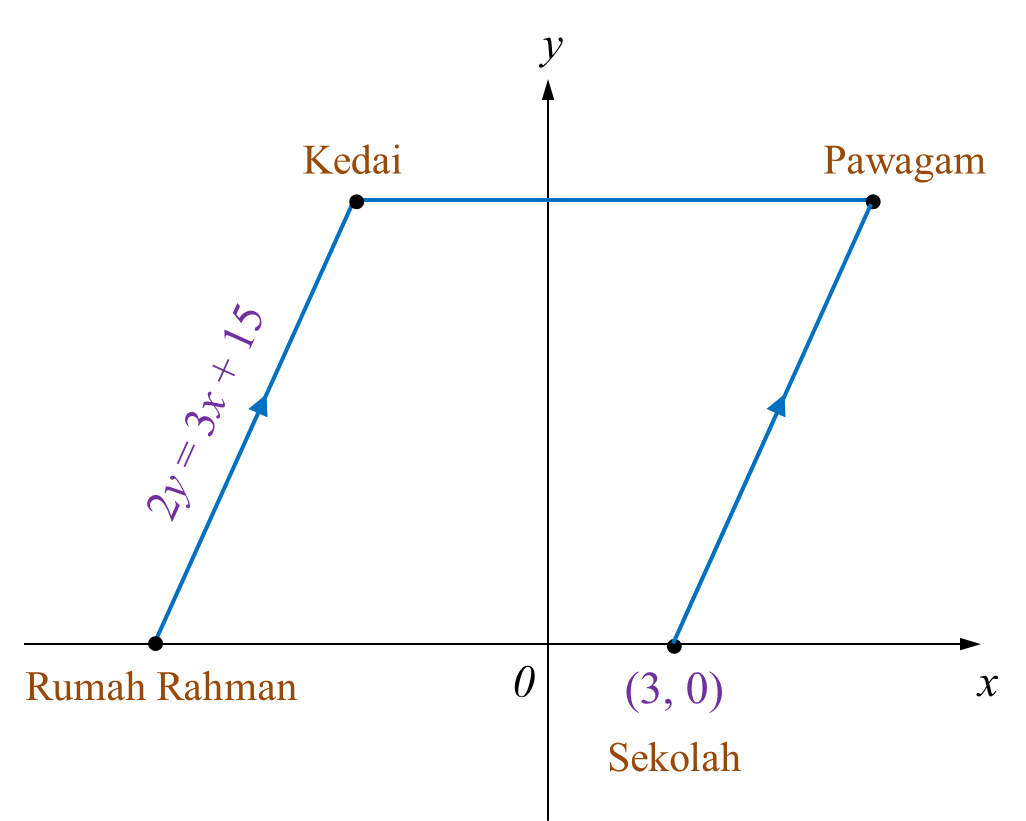
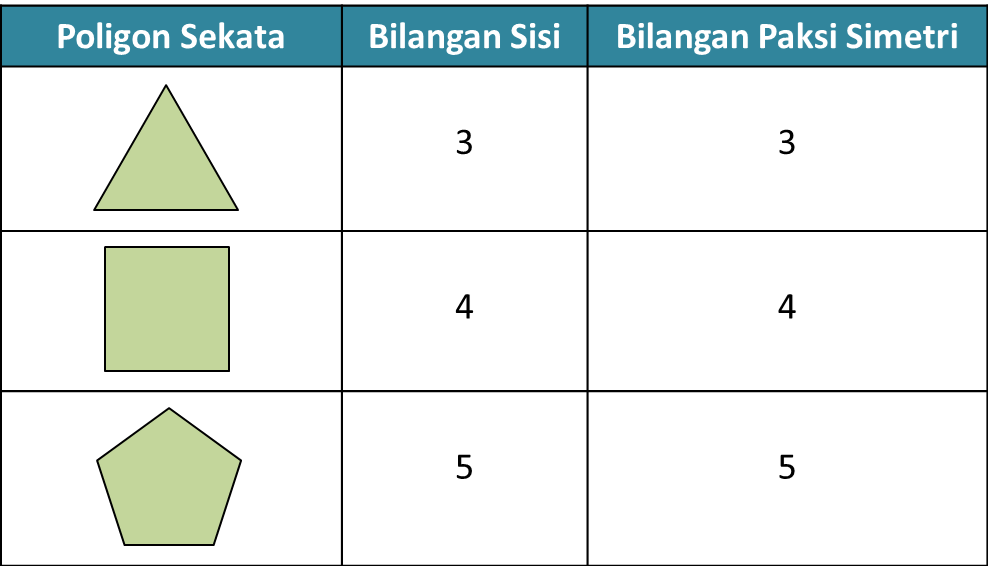 Jadual 1
Jadual 1 Rajah 7
Rajah 7


 Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.
Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.