Bab 14 Penjelmaan

Posted on May 5, 2016 by user

3.1 Gabungan Dua Penjelmaan

3.1a Menentukan Imej suatu Objek bagi Gabungan Dua Penjelmaan Isometri

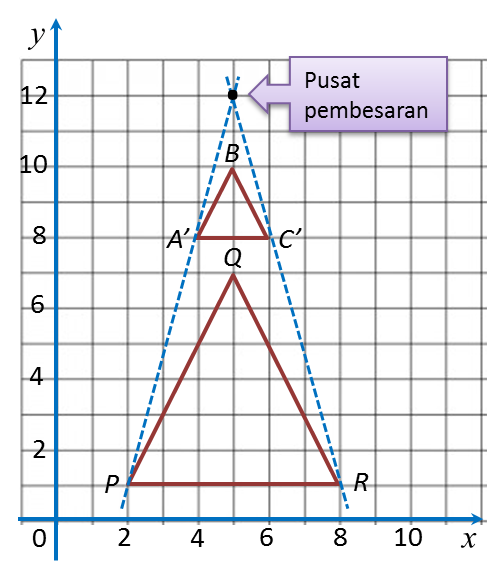
1. Translasi, pantulan dan putaranadalah penjelmaan isometri.

2. Dalam suatu penjelmaan isometri, bentukdan saiz bagi imej adalah sama dengan objek.

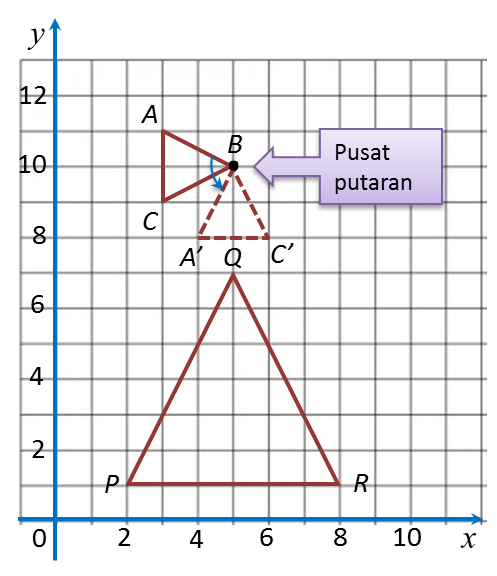
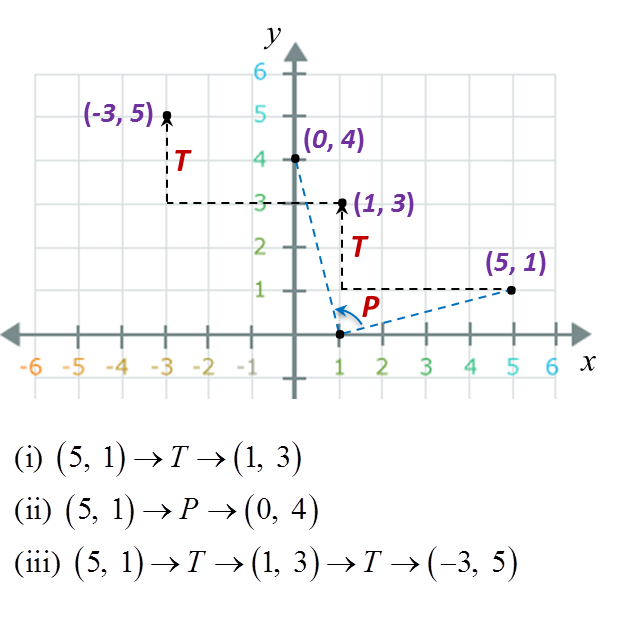
3. Bagi dua penjelmaan, A dan B,

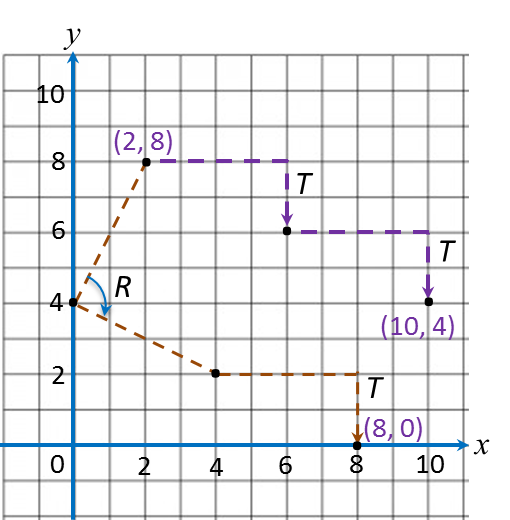
(a) Gabungan penjelmaan AB bermaksud penjelmaan B diikuti dengan penjelmaan A.

(b) Gabungan penjelmaan BA bermaksud penjelmaan A diikuti dengan penjelmaan B.

(c) Gabungan penjelmaan A² = AA bermaksud penjelmaan A dijalankan dua kali berturut-turut.

Bab 14 Penjelmaan

Posted on May 5, 2016 by user

3.1b Menentukan Imej suatu Objek bagi Gabungan Penjelmaan yang Melibatkan (a) Dua Pembesaran, (b) Satu Pembesaran dengan Satu daripada Penjelmaan Isometri

Pembesaran ialah suatu penjelmaan di mana semua titik objek bergerak dari satu titik tetap, mengikut suatu nisbah tertentu.

1. Titik tetap tersebut adalah pusat pembesaran manakala nisbah tertentu dikenali sebagai faktor skala.

\begin{array}{l} Faktor skala, k \\ = \frac{jarak titik pada imej dari pusat pembesaran}{\begin{array}{l} jarak titik yang sepadan pada \\ objek dari pusat pembesaran \end{array}} \end{array}

2. Bagi pembesaran, objek dan imej adalah serupa.

3. Luas imej = (Faktor skala)²× Luas objek

= k² × Luas objek

Contoh:

E, P dan T ialah tiga penjelmaan yang ditakrifkan seperti berikut:

E = Pembesaran pada pusat V (0, –1) dengan factor skala 2.

P = Pantulan pada garis lurus y = –1 .

T = T r a n s l a s i (\begin{array}{l} 3 \\ - 3 \end{array})

Berdasarkan rajah di atas, tentukan imej bagi trapezium berlorek di bawah gabungan penjelmaan

(a) E²
(b) ET
(c) EP

Penyelesaian:

(a)

Trapezium berlorek → (E) trapezium III → (E) trapezium D.

Maka, imej bagi trapezium berlorek di bawah gabungan penjelmaan E² = EE ialah trapezium D.

(b)

Trapezium berlorek → (T) trapezium II → (E) trapezium A.

Maka, imej bagi trapezium berlorek di bawah gabungan penjelmaan ET ialah trapezium A.

(c)

Trapezium berlorek → (P) trapezium I → (E) trapezium B.

Maka, imej bagi trapezium berlorek di bawah gabungan penjelmaan EP ialah trapezium B.

Bab 14 Penjelmaan

Posted on May 4, 2016 by user

3.2 Menyelesaikan Masalah yang Melibatkan Penjelmaan

Contoh:

Rajah di bawah menunjukkan segi tiga ABC, SQT dan PQR.

(a) Penjelmaan T ialah translasi

(\begin{array}{l} 5 \\ - 2 \end{array})

Penjelmaan P ialah pantulan pada garis lurus y = 7.

Nyatakan koordinat imej bagi titik A di bawah setiap penjelmaan berikut:
(i) Penjelmaan T,
(ii) Gabungan penjelmaan PT.

(b) (i) PQR ialah imej bagi segi tiga ABC di bawah gabungan penjelmaan MN. Huraikan selengkapnya penjelmaan N dan penjelmaan M.

(ii) Diberi bahawa luas bagi rantau berlorek PSTR ialah 200 m². Hitungkan luas segi tiga SQT.

Penyelesaian:

(a)(i) A(3, 11) → T → A’(8, 9).

(a)(ii) A(3, 11) → T → A’(8, 9) → P → A”(8, 5).

(b)(i)

N = Putaran lawan arah jam melalui 90^o pada pusat B (5, 10).

(b)(ii)

M = Pembesaran pada pusat (5, 12) dengan faktor skala 3.

(c)

Luas imej = (factor skala)² × Luas objek

Luas PQR = 3² × Luas SQT

Luas SQT + Luas PSTR = 9 × Luas SQT

Luas SQT + 200 = 9 × Luas SQT

200 = (9 × Luas SQT) – Luas SQT

200 = 8 × Luas SQT

Luas S Q T = \frac{200}{8}

Luas SQT = 25 m²

3.4.2 SPM Praktis, Penjelmaan (Soalan Panjang)

Posted on May 4, 2016 by user

3.4.2 SPM Praktis, Penjelmaan (Soalan Panjang)

Soalan 2:

(a) Penjelmaan P ialah pantulan pada garis lurus x = m.

Penjelmaan T ialah translasi

(\begin{array}{l} 4 \\ - 2 \end{array})

Penjelmaan R ialah putaran 90^o ikut arah jam pada pusat (0, 4).
(i) Titik (6, 4) adalah imej bagi titik ( –2, 4) di bawah penjelmaan P.
(ii) Cari koordinat imej bagi titik (2, 8) di bawah gabungan penjelmaan berikut:

(a) T²,

(b) TR.

(b) Rajah di bawah menunjukkan trapezium CDFE dan trapezium HEFG dilukis pada suatu satah Cartesian.

(i) HEFG ialah imej bagi CDEF di bawah gabungan penjelmaan WU.

Huraikan selengkapnya penjelmaan:
(a) U
(b) W

(ii) Diberi bahawa CDEF mewakili suatu kawasan yang mempunyai luas 60 m².
Hitungkan luas, dalam m², kawasan yang diwakili oleh rantau berlorek.

Penyelesaian:

(a)(i)

\begin{array}{l} (6, 4) \to P \to (- 2, 4) \\ m = \frac{6 + (- 2)}{2} = 2 \end{array}

(a)(ii)

(a) (2, 8) → T → (6, 6) → T → (10, 4)

(b) (2, 8) → R → (4, 2) → T → (8, 0)

(b)(i)(a)

U: Putaran lawan arah jam melalui 90^o pada pusat A (3, 3).

(b)(i)(b)

Faktor skala = \frac{H E}{C D} = \frac{4}{2} = 2

W: Satu pembesaran pada pusat B (3, 5) dengan faktor skala 2.

(b)(ii)

Luas HEFG = (factor skala)² × Luas objek

= 2² × luas CDEF

= 4 × 60
= 240 m²

Oleh itu,

Luas rantau berlorek

= Luas HEFG – luas CDEF

= 240 – 60

= 180 m²

3.4.1 SPM Praktis, Penjelmaan (Soalan Panjang)

Posted on May 4, 2016 by user

SPM Praktis, Penjelmaan (Soalan Panjang)

Soalan 1:

(a) Penjelmaan T ialah translasi

(\begin{array}{l} - 4 \\ 2 \end{array})

dan penjelmaan P ialah putaran 90^o lawan arah jam pada pusat (1, 0).

Nyatakan koordinat imej bagi titik (5, 1) di bawah setiap penjelmaan berikut:

(i) Translasi T,

(ii) Putaran P,

(iii) Gabungan penjelmaan T².

(b) Rajah di bawah menunjukkan tiga sisi empat, ABCD, EFGH dan JKLM, dilukis pada suatu satah Cartesian.

(i) JKLM ialah imej bagi ABCD di bawah gabungan penjelmaan VW.

Huraikan selengkapnya penjelmaan:

(a) W (b) V

(ii) Diberi bahawa sisi empat ABCD mewakili suatu kawasan yang mempunyai luas 18 m².

Hitungkan luas, dalam m², kawasan yang diwakili oleh rantau berlorek.

Penyelesaian:

(a)

(b)

(i)(a)

W: Satu pantulan pada garis lurus x = –2

(i)(b)

V: Satu pembesaran pada pusat (0, 4) dengan faktor skala 3.

(b)(ii)

Luas EFGH = luas ABCD = 18 m²

Luas JKLM = (factor skala)² × Luas objek

= 3² × luas EFGH

= 3² × 18

= 162 m²

Oleh itu,

Luas rantau berlorek

= Luas JKLM – luas EFGH

= 162 – 18

= 144 m²