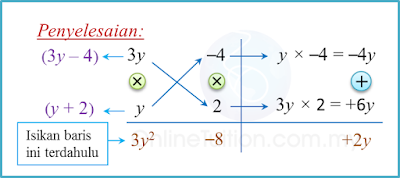
Soalan 17 (4 markah):
Hitung nilai x dan nilai y yang memuaskan persamaan linear serentak berikut:
2x + y = 8
–x + 4y = 5
Penyelesaian:
2x+y=8............... (1)−x+4y=5 ............... (2)(2)×2: −2x+8y=10 ............... (3)(1)+(3): y+8y=8+109y=18y=189y=2Dari (1):2x+2=82x=8−22x=6x=62x=3∴
Hitung nilai x dan nilai y yang memuaskan persamaan linear serentak berikut:
2x + y = 8
–x + 4y = 5
Penyelesaian:
2x+y=8............... (1)−x+4y=5 ............... (2)(2)×2: −2x+8y=10 ............... (3)(1)+(3): y+8y=8+109y=18y=189y=2Dari (1):2x+2=82x=8−22x=6x=62x=3∴
Soalan 18 (4 markah):
Sebuah akuarium mempunyai panjang (x + 7) cm, lebar x cm dan tinggi 60 cm.
Jumlah isi padu akuarium itu ialah 48000 cm3. Akuarium itu akan diisi penuh dengan air.
Hitung nilai x.
Penyelesaian:
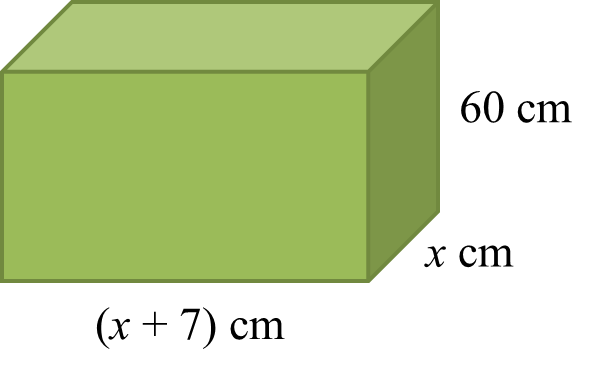
Sebuah akuarium mempunyai panjang (x + 7) cm, lebar x cm dan tinggi 60 cm.
Jumlah isi padu akuarium itu ialah 48000 cm3. Akuarium itu akan diisi penuh dengan air.
Hitung nilai x.
Penyelesaian:

 Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.
Diberi bahawa panjang kolam adalah 3 kali lebar kolam itu.