Question 6:
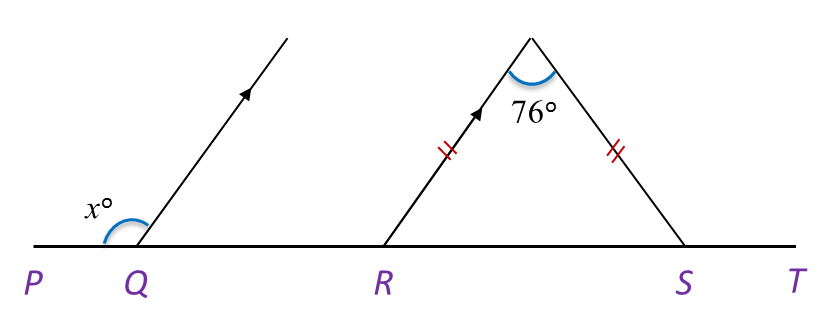
In Diagram below, PQRST is a straight line. Find the value of x.
Solution:
Interior angle of R=(180o−76o)÷2=52o∠x=exterior angle of R (corresponding angles)Hence, x=76o+52o=128o
In Diagram below, PQRST is a straight line. Find the value of x.

Solution:
Interior angle of R=(180o−76o)÷2=52o∠x=exterior angle of R (corresponding angles)Hence, x=76o+52o=128o
Question 7:
In Diagram below, find the value of y.

Solution:
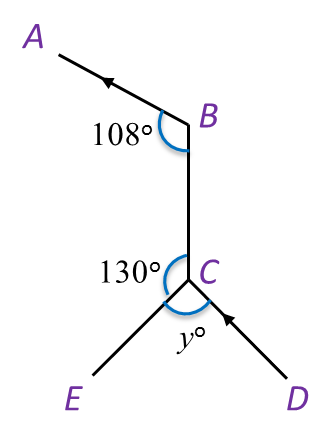
∠ABC=∠BCD =108o (alternate angle)yo+130o+108o=360o yo=360o−238o yo=122o
In Diagram below, find the value of y.

Solution:

∠ABC=∠BCD =108o (alternate angle)yo+130o+108o=360o yo=360o−238o yo=122o
Question 8:
In Diagram below, PSR and QST are straight lines.
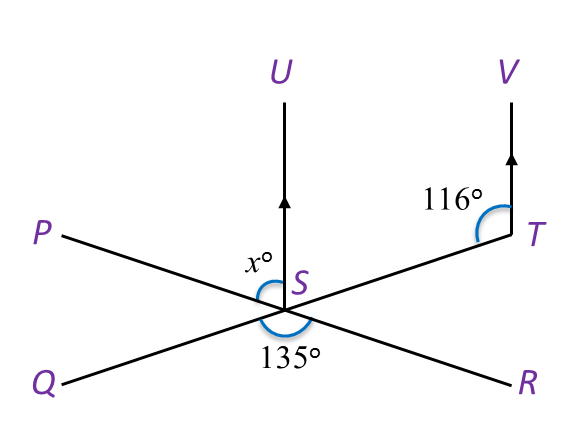 Find the value of x.
Find the value of x.
Solution:
∠UST+∠STV=180o∠UST=180o−116o=64o∠PST=∠QSRxo+∠UST=135oxo+∠UST=135oxo=71ox=71
In Diagram below, PSR and QST are straight lines.
 Find the value of x.
Find the value of x.Solution:
∠UST+∠STV=180o∠UST=180o−116o=64o∠PST=∠QSRxo+∠UST=135oxo+∠UST=135oxo=71ox=71
Question 9:
In Diagram below, PWV is a straight line.
 (a) Which line is perpendicular to line PWV?
(a) Which line is perpendicular to line PWV?
(b) State the value of ∠ RWU.
Solution:
(a) SW
(b) ∠ RWU = 13o + 29o + 20o = 62o
In Diagram below, PWV is a straight line.
 (a) Which line is perpendicular to line PWV?
(a) Which line is perpendicular to line PWV?(b) State the value of ∠ RWU.
Solution:
(a) SW
(b) ∠ RWU = 13o + 29o + 20o = 62o
Question 10:
In Diagram below, UVW is a straight line.

(a) Which line is parallel to line TU?
(b) State the value of ∠ QVS.
Solution:
(a) QV
(b) ∠ QVS = 8o + 18o = 26o
In Diagram below, UVW is a straight line.

(a) Which line is parallel to line TU?
(b) State the value of ∠ QVS.
Solution:
(a) QV
(b) ∠ QVS = 8o + 18o = 26o


 h2 = 32 + 42
h2 = 32 + 42 
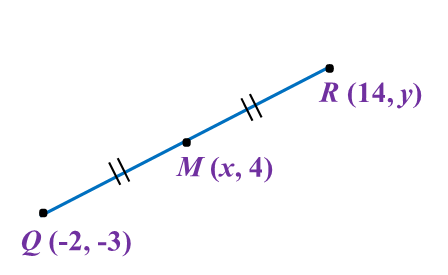 The value of x and y are
The value of x and y are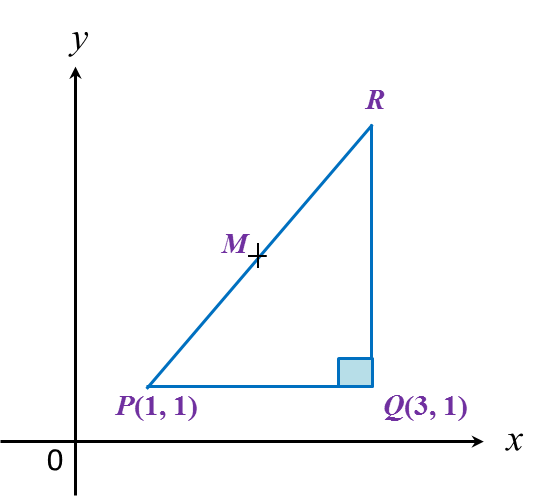
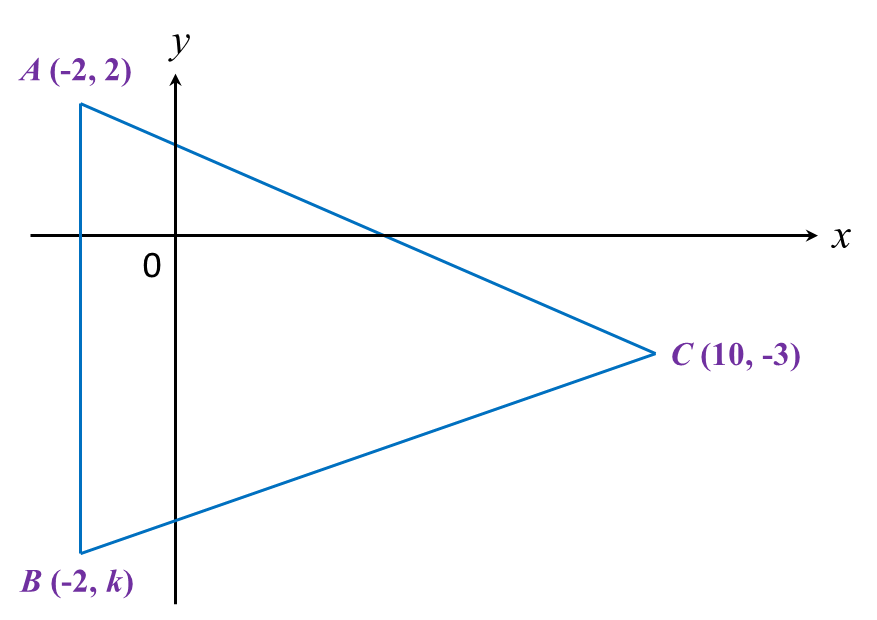
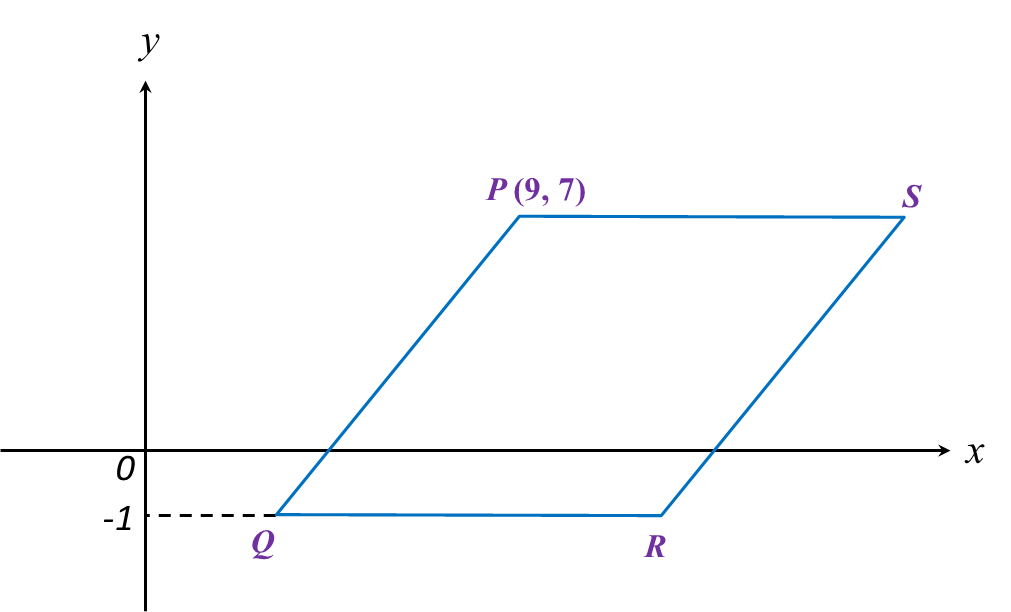
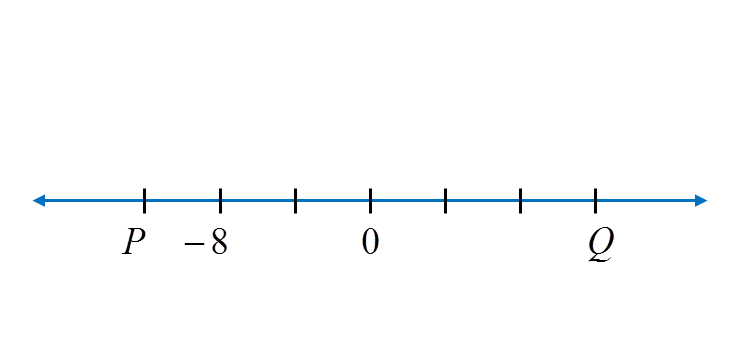 What is the value of P and of Q?
What is the value of P and of Q?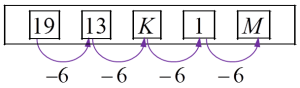
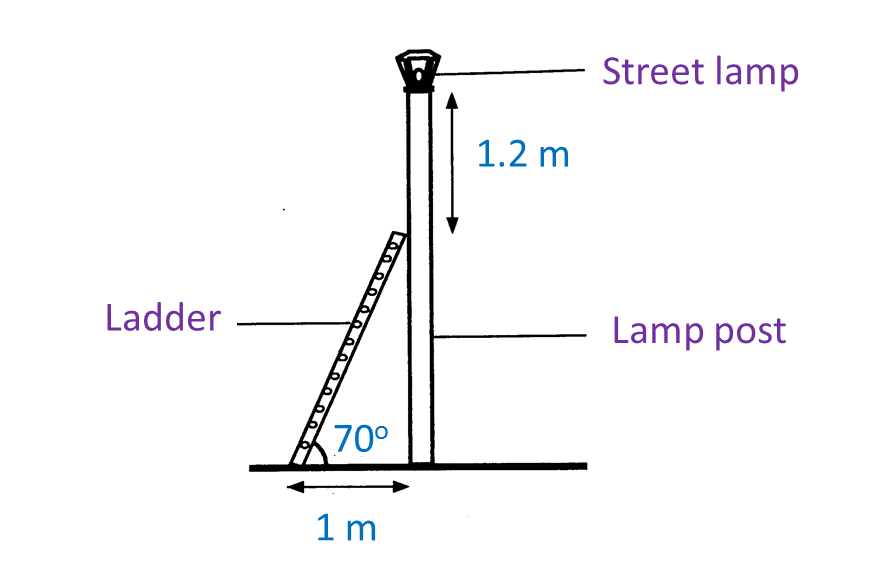 (a) What is the length, in m, of the ladder?
(a) What is the length, in m, of the ladder?