Question 6:
The point M (x, 4), is the midpoint of the line joining straight line Q (-2, -3) and R (14, y).
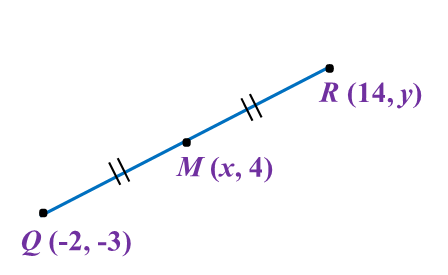 The value of x and y are
The value of x and y are
Solution:
x=−2+142x=122x=64=−3+y28=−3+yy=11
The point M (x, 4), is the midpoint of the line joining straight line Q (-2, -3) and R (14, y).
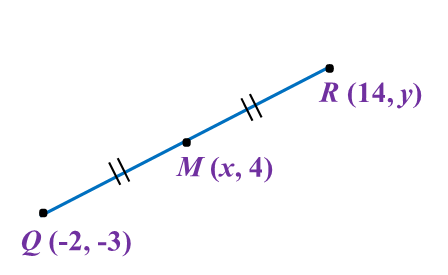 The value of x and y are
The value of x and y areSolution:
x=−2+142x=122x=64=−3+y28=−3+yy=11
Question 7:
In diagram below, PQR is a right-angled triangle. The sides QR and PQ are parallel to the y-axis and the x-axis respectively. The length of QR = 6 units.
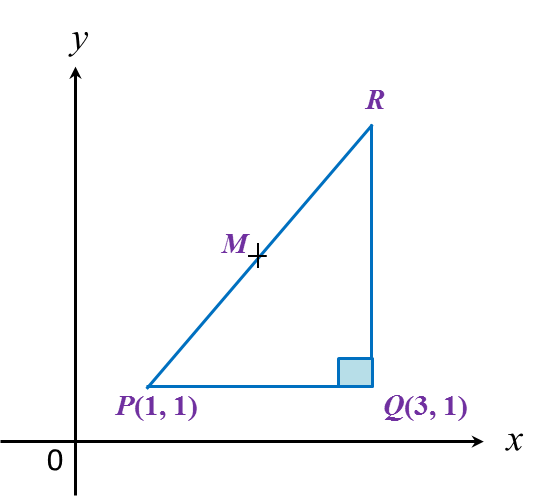
Given that M is the midpoint of PR, then the coordinates of M are
Solution:
x-coordinate of R = 3
y-coordinate of R = 1 + 6 = 7
R = (3, 7)
P(1,1),R(3,7)Coordinates of M=(1+32,1+72)=(2,4)
In diagram below, PQR is a right-angled triangle. The sides QR and PQ are parallel to the y-axis and the x-axis respectively. The length of QR = 6 units.

Given that M is the midpoint of PR, then the coordinates of M are
Solution:
x-coordinate of R = 3
y-coordinate of R = 1 + 6 = 7
R = (3, 7)
P(1,1),R(3,7)Coordinates of M=(1+32,1+72)=(2,4)
Question 8:
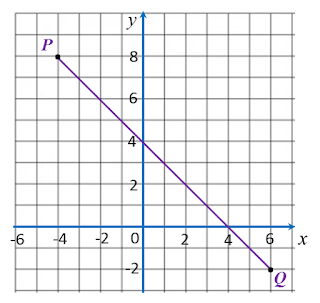
Given points P (–2, 8) and Q (10, 8), find the length of PQ.
Solution:
Length of PQ=√[10−(−2)]2+(8−8)2=√(14)2+0=14 units
Given points P (–2, 8) and Q (10, 8), find the length of PQ.
Solution:
Length of PQ=√[10−(−2)]2+(8−8)2=√(14)2+0=14 units
Question 9:
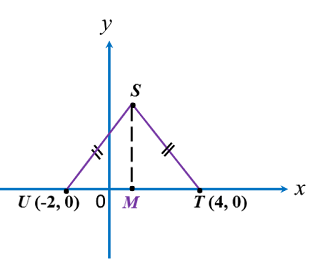
In diagram below, ABC is an isosceles triangle.
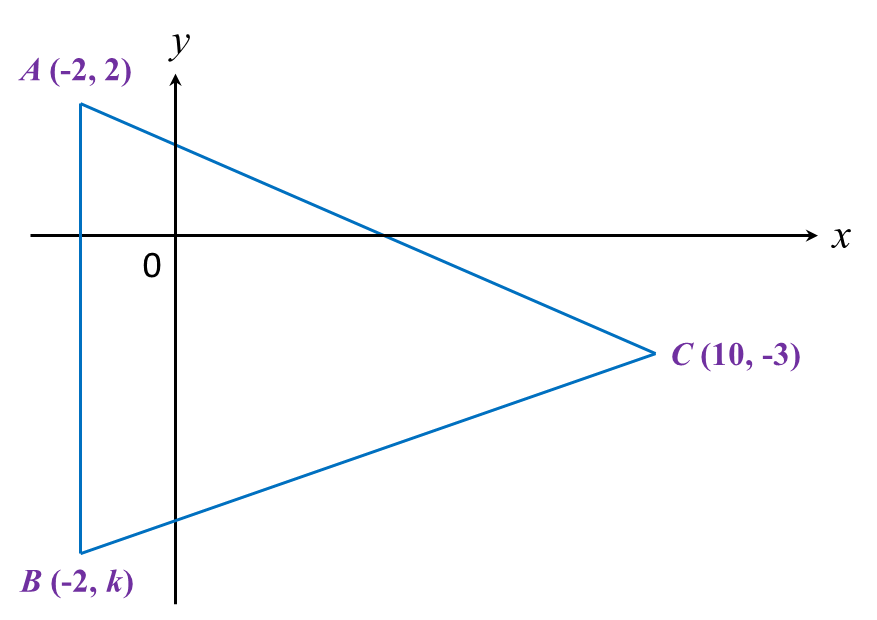
Find
(a) the value of k,
(b) the length of BC.
Solution:
(a)For an isosceles triangle, y−coordinate of C is the midpoint of straight line AB.2+k2=−32+k=−6 k=−8(b)B=(−2,−8)BC=√[10−(−2)]2+[−3−(−8)]2 =√122+52 =13 units
In diagram below, ABC is an isosceles triangle.

Find
(a) the value of k,
(b) the length of BC.
Solution:
(a)For an isosceles triangle, y−coordinate of C is the midpoint of straight line AB.2+k2=−32+k=−6 k=−8(b)B=(−2,−8)BC=√[10−(−2)]2+[−3−(−8)]2 =√122+52 =13 units
Question 10:
Diagram below shows a rhombus PQRS drawn on a Cartesian plane. PS is parallel to x-axis.
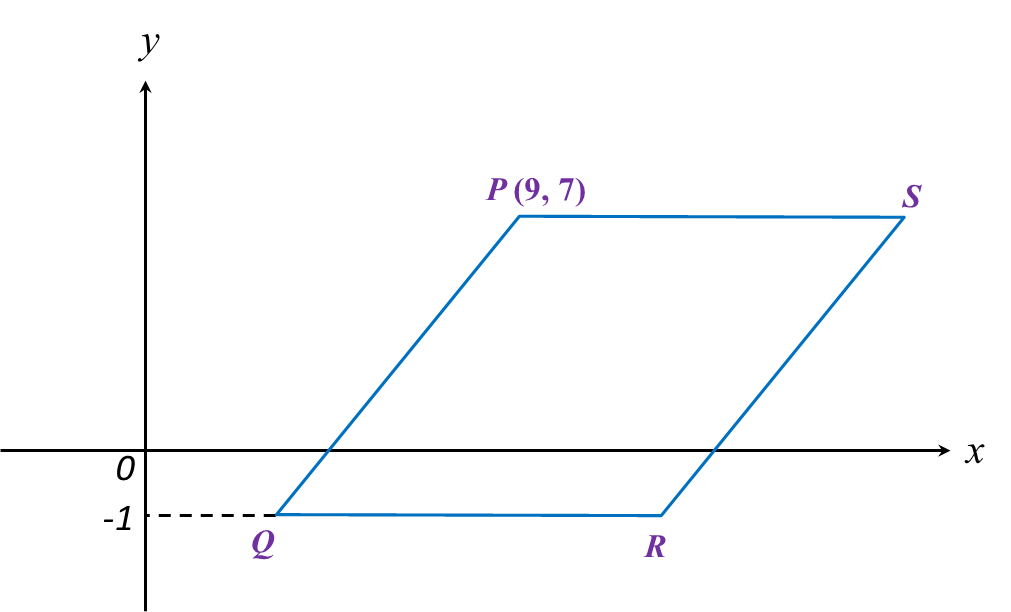
Given the perimeter of PQRS is 40 units, find the coordinates of point R.
Solution:
All sides of rhombus have the same length,therefore length of each side=404=10 unitsPQ=10(9−x1)2+(7−(−1))2=10281−18x1+x12+64=100x12−18x1+45=0(x1−3)(x1−15)=0x1=3,15x1=3Q=(3,−1),R=(x2,−1)QR=10(x2−3)2+[−1−(−1)]2=102x22−6x2+9+0=100x22−6x2−91=0(x2+7)(x2−13)=0x2=−7,13x2=13∴
Diagram below shows a rhombus PQRS drawn on a Cartesian plane. PS is parallel to x-axis.

Given the perimeter of PQRS is 40 units, find the coordinates of point R.
Solution:
All sides of rhombus have the same length,therefore length of each side=404=10 unitsPQ=10(9−x1)2+(7−(−1))2=10281−18x1+x12+64=100x12−18x1+45=0(x1−3)(x1−15)=0x1=3,15x1=3Q=(3,−1),R=(x2,−1)QR=10(x2−3)2+[−1−(−1)]2=102x22−6x2+9+0=100x22−6x2−91=0(x2+7)(x2−13)=0x2=−7,13x2=13∴
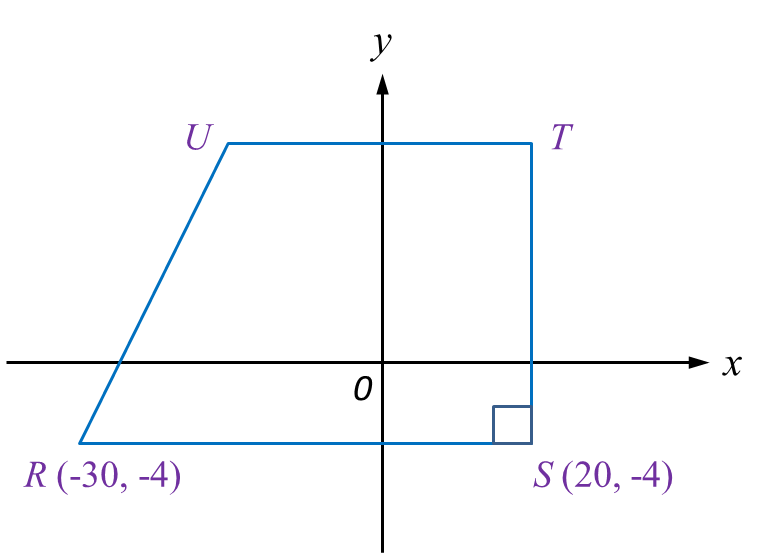
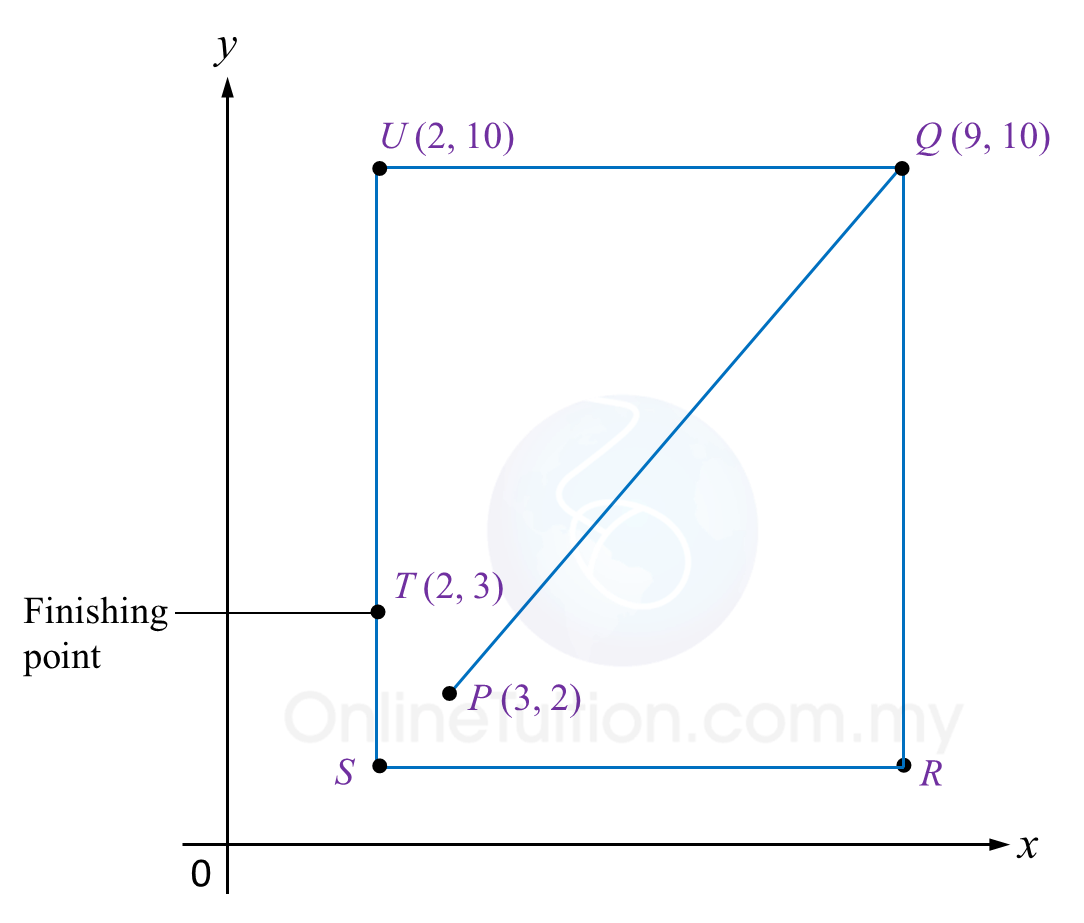 The route of male participants is PQUT while the route for female participants is QRST. QR is parallel to UT whereas UQ is parallel to SR.
The route of male participants is PQUT while the route for female participants is QRST. QR is parallel to UT whereas UQ is parallel to SR.