Question 1:
Evaluate 5 + (–7)   

Solution:

Therefore,
5 + (–7) = 5 – 7
= –2

Question 2:
Evaluate –6 – (–5)   

Solution:

Therefore,
–6 – (–5) = –6 + 5   
= –1

Question 3:
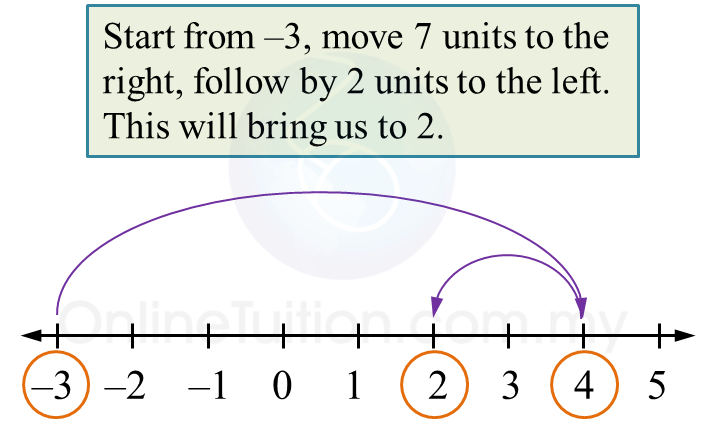
Simplify –3 + 7 + (–2)
 
Solution:


Therefore,
–3 + 7 + (–2) = 4 + (–2)
= 4 – 2
= 2

Question 4:
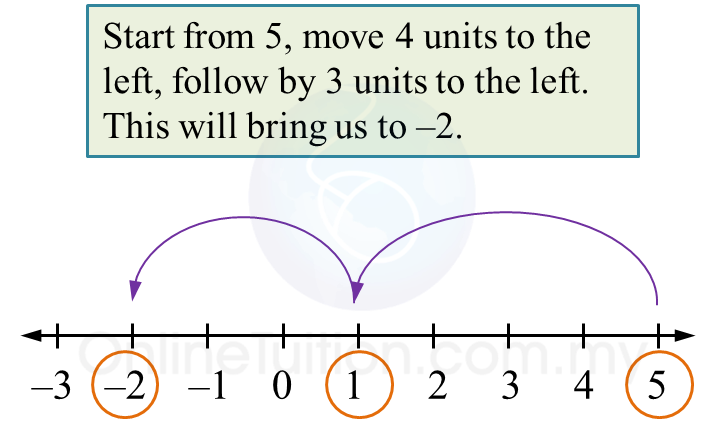
Simplify 5 + (–4) + (–3)  

Solution:


Therefore,
5 + (–4) + (–3)
= 5 – 4 – 3
= –2

6.2 Addition and Subtraction of Integers

6.2.1 Addition of Integers
1. Addition of integers can be done on a number line.
(a) To add a positive integer:
Move to the right (positive direction) on the number line.

(b) To add a negative integer:
Move to the left (negative direction) on the number line.



2. Integers with the same signs are called integers with like signs.
Example:
2 and 7, –25 and –5.

3. Integers with the different signs are called integers with unlike signs.
Example:
+2 and –7, –25 and 5.

Example 1:
Solve the following.
(a) 3 + (+4)
(b) 2 + (–5)

Solution:
(a)

Therefore,
3 + (+4) = 3 + 4
= 7

(b)
Therefore,
2 + (–5)
= –3