2.2.1 Squares, Square Roots, Cube and Cube Roots, PT3 Practice 1
Question 1:
Calculate the values of the following:
(a)√5098(b)√11764(c)√81−√0.01(d)√3.24
Solution:
(b)√11764=√8164=98=118
(c)√81−√0.01=9−√1100=9−110=9−0.1=8.9
(d)√3.24=√324100=√3625=√8125=95=145
Question 2:
Calculate the values of the following:
(a)3√16250(b)3√−4256(c)3√0.008(d)3√0.729
Solution:
(b)3√−4256=3√−164=−14
(c)3√0.008=3√81000=210=0.2
(d)3√−0.729=3√−7291000=−910=−0.9
Question 3:
Find the value of
3√338+√21425.
Solution:
Question 4:
Find the values of the following:
(a) 1 – (–0.3)3.
(b)
(2.1÷3√27)2
Solution:
(a)
1 – (–0.3)3 = 1 – [(–0.3) × (–0.3) × (–0.3)]
= 1 – (–0.027)
= 1 + 0.027
= 1.027
(b)
(2.1÷3√27)2=(2.1÷3)2=(0.7)2=0.49
Question 5:
Find the values of the following:
(a)(9+3√−8)2(b)√144÷3√216×0.33
Solution:
(b)√144÷3√216×0.33=144÷6×(0.3×0.3×0.3)=24×0.027=0.648

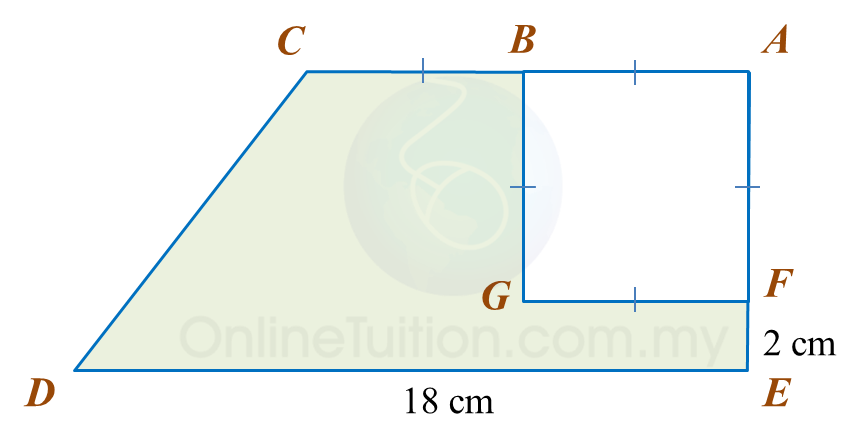
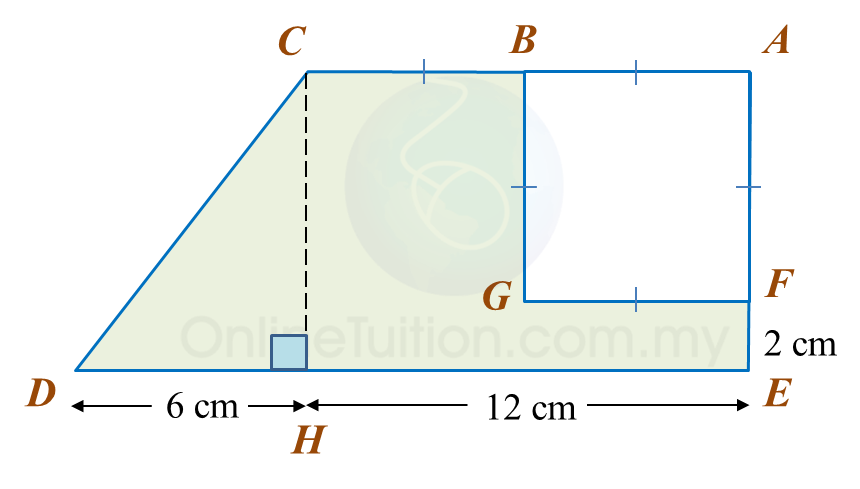
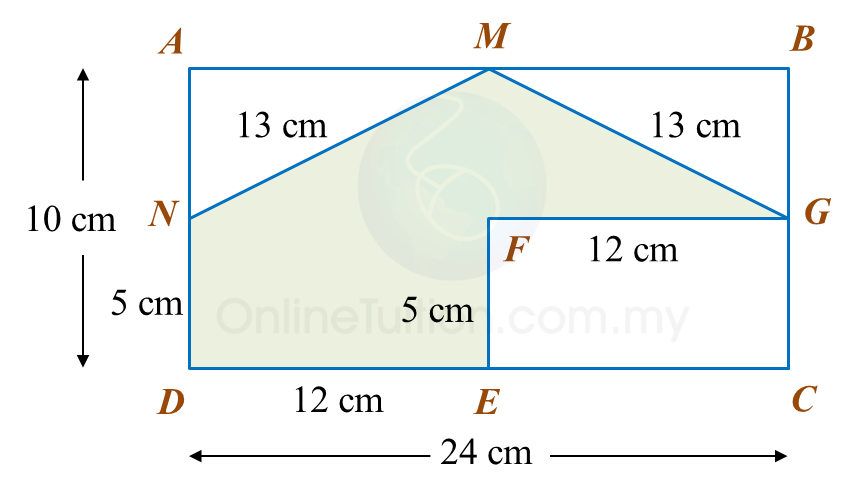
 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.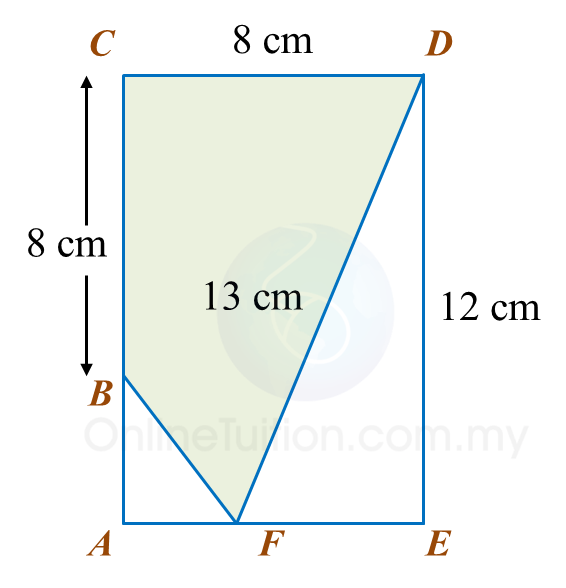
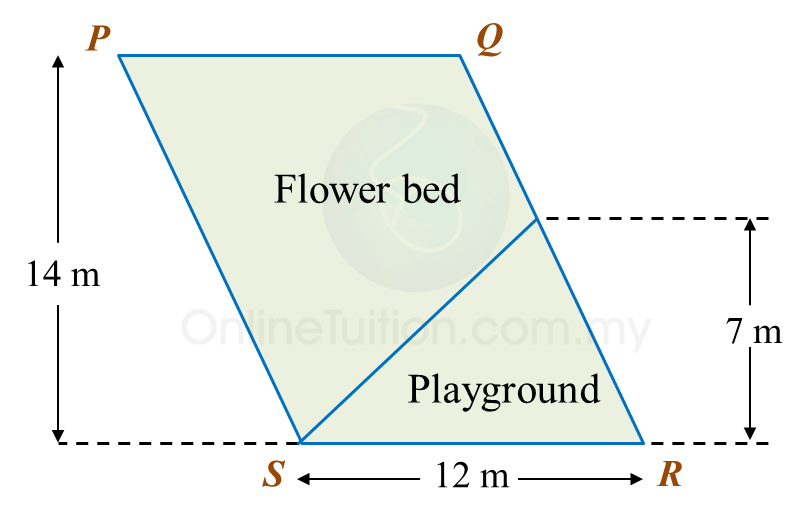 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.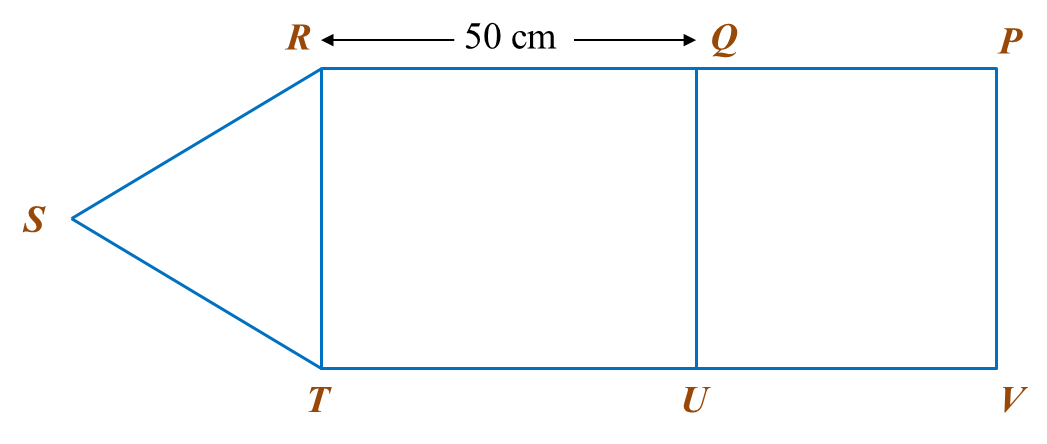
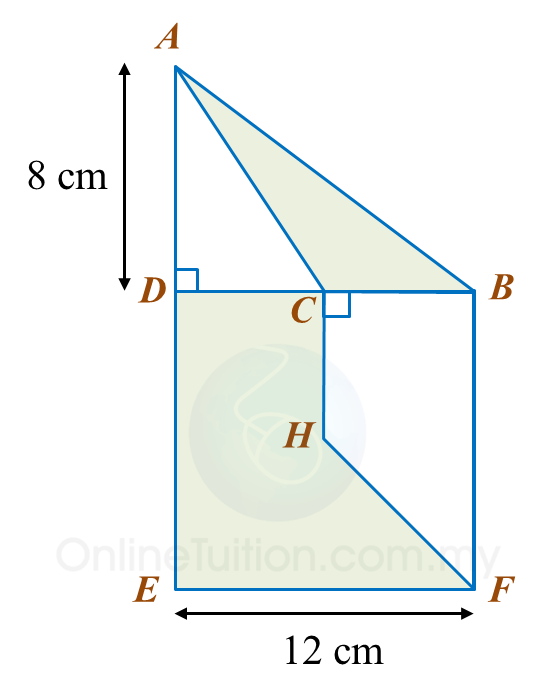
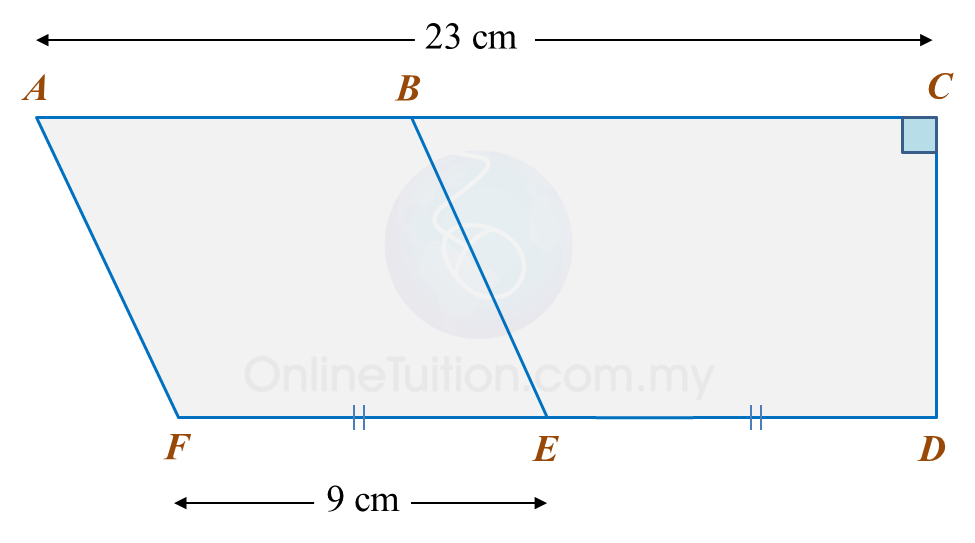 The area of ABEF is 72 cm2.
The area of ABEF is 72 cm2.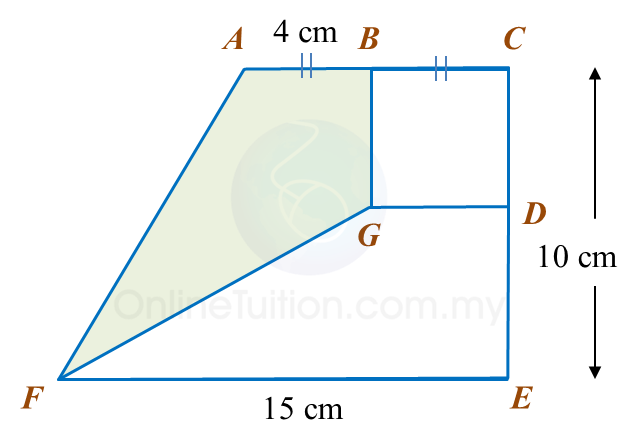
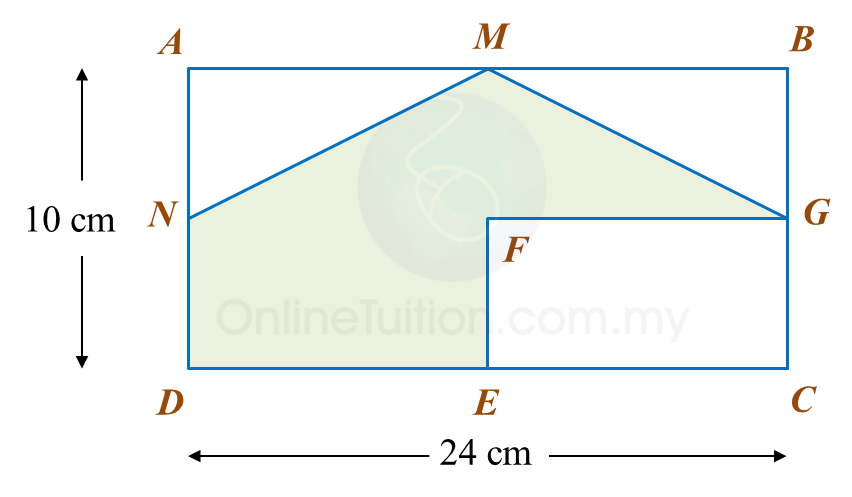
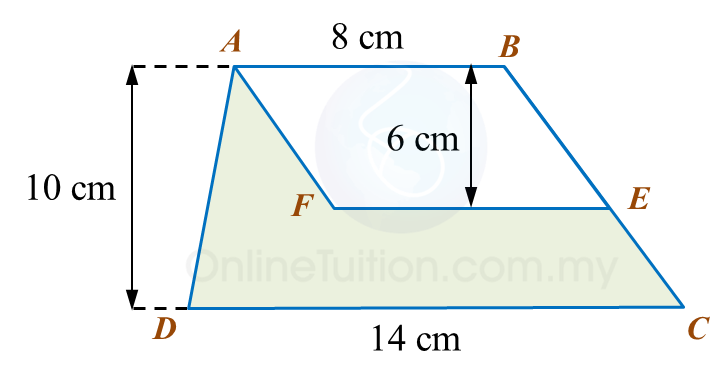 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
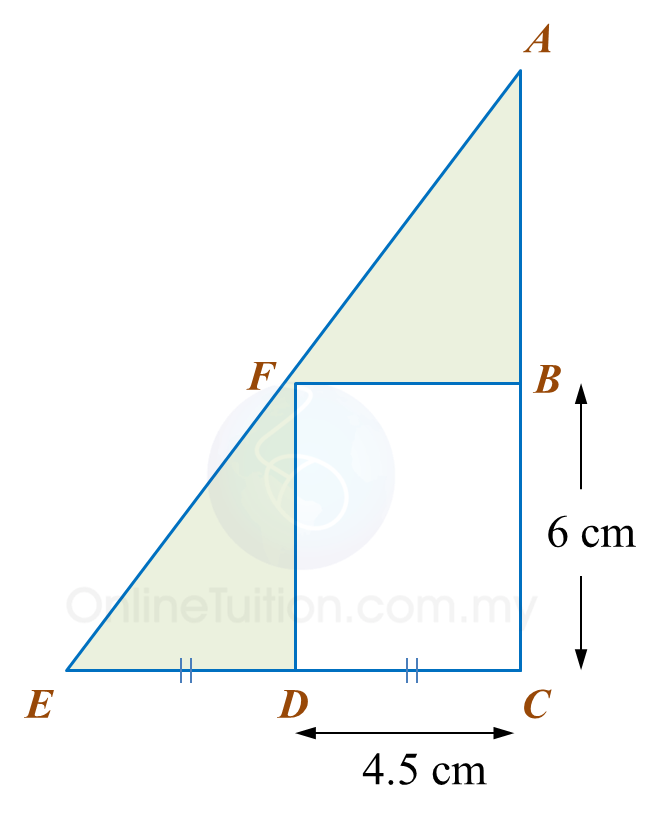 Calculate
Calculate