[adinserter name="Block 3"]
Question 1:
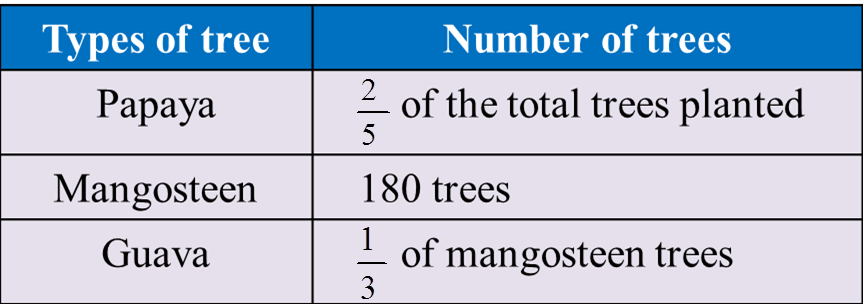
Karen has 18 m of ribbon to tie 16 bars of chocolate and 28 boxes of sweets. A bar of chocolate needs 24 cm of ribbon and a box of sweets needs 38 cm of ribbon.
Calculate the length, in m, of the remaining ribbon.
Solution:
Length of ribbon needed
= (16 × 24 cm) + (28 × 38 cm)
= 384 cm + 1064 cm
= 1448 cm
= 14.48 m
Length of remaining ribbon
= 18 m – 14.48 m
= 3.52 m
Karen has 18 m of ribbon to tie 16 bars of chocolate and 28 boxes of sweets. A bar of chocolate needs 24 cm of ribbon and a box of sweets needs 38 cm of ribbon.
Calculate the length, in m, of the remaining ribbon.
Solution:
Length of ribbon needed
= (16 × 24 cm) + (28 × 38 cm)
= 384 cm + 1064 cm
= 1448 cm
= 14.48 m
Length of remaining ribbon
= 18 m – 14.48 m
= 3.52 m
[adinserter name="Block 3"]
Question 2:
The length of a red string is 4 m 80 cm. The length of a brown string is ⅔ of the length of the red string. The length of a black string is twice the length of the brown string.
Calculate the total length, in m, of the brown and the black strings.
Solution:
Length of brown string=23×4 m 80 cm=23×4.8=3.2 mLength of black string=2×3.2 m=6.4 mTotal length=3.2 m+6.4 m=9.6 m
The length of a red string is 4 m 80 cm. The length of a brown string is ⅔ of the length of the red string. The length of a black string is twice the length of the brown string.
Calculate the total length, in m, of the brown and the black strings.
Solution:
Length of brown string=23×4 m 80 cm=23×4.8=3.2 mLength of black string=2×3.2 m=6.4 mTotal length=3.2 m+6.4 m=9.6 m
[adinserter name="Block 3"]
Question 3:
Kelly has 13 m of cloth. She uses it to make 6 curtains and 4 tablecloths. Each curtain requires 1.25 m of cloth and each tablecloth requires 90 cm of cloth.
What is the length, in m, of the remaining cloth?
Solution:
Length of cloth used to make curtains
= 6 × 1.25 m
= 7.5 m
Length of cloth used to make tablecloth
= 4 × 90 cm
= 360 cm
= 3.6 m
Length of the remaining cloth
= 13 – 7.5 – 3.6
= 1.9 m
Kelly has 13 m of cloth. She uses it to make 6 curtains and 4 tablecloths. Each curtain requires 1.25 m of cloth and each tablecloth requires 90 cm of cloth.
What is the length, in m, of the remaining cloth?
Solution:
Length of cloth used to make curtains
= 6 × 1.25 m
= 7.5 m
Length of cloth used to make tablecloth
= 4 × 90 cm
= 360 cm
= 3.6 m
Length of the remaining cloth
= 13 – 7.5 – 3.6
= 1.9 m
[adinserter name="Block 3"]
Question 4:
A rope measuring 6 m 30 cm is cut into 1.6 m, 96 cm and the remainder into two equal parts. Find the length of each of the remaining parts, in cm.
Solution:
(6 m 30 cm – 1.6 m – 96 cm) ÷ 2
= (630 cm – 160 cm – 96 cm) ÷ 2
= 374 cm ÷ 2
= 187 cm
A rope measuring 6 m 30 cm is cut into 1.6 m, 96 cm and the remainder into two equal parts. Find the length of each of the remaining parts, in cm.
Solution:
(6 m 30 cm – 1.6 m – 96 cm) ÷ 2
= (630 cm – 160 cm – 96 cm) ÷ 2
= 374 cm ÷ 2
= 187 cm


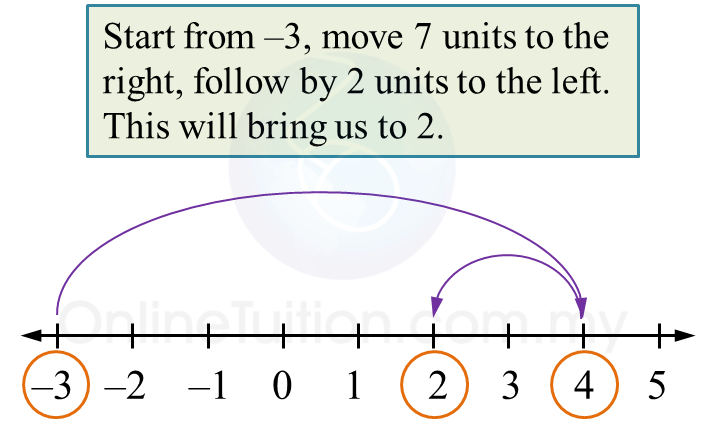
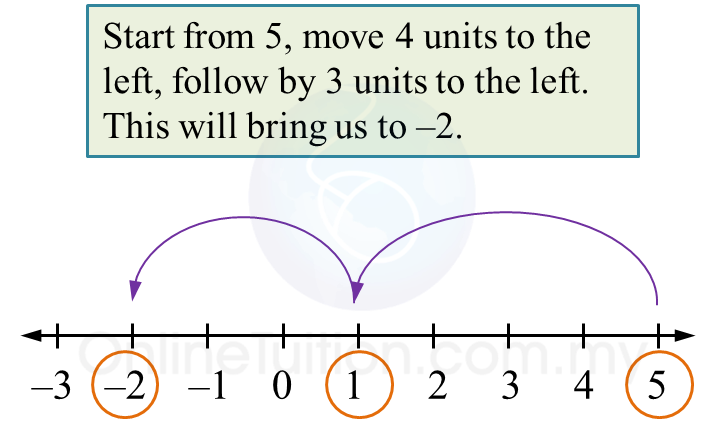

 Therefore,
Therefore, Therefore,
Therefore,