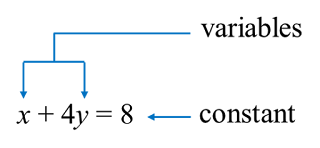
12.2.2 Linear Inequalities, PT3 Focus Practice

Posted on May 20, 2018 by user

Question 6:
List all the integer values of x which satisfy the following linear inequalities:
–2 < 3x + 1 ≤ 10

Solution:
–2 < 3x + 1
–3 < 3x
x > –1
x = 0, 1, 2, 3, …

3x + 1 ≤ 10
3x ≤ 9
x ≤ 3
x = 3, 2, 1, 0, …

Therefore x = 0, 1, 2, 3

Question 7:
List all the integer values of x which satisfy the following linear inequalities:
–5 < 2x – 3 ≤ 1

Solution:
–5 < 2x – 3
–5 + 3 < 2x
2x > –2
x > –1
x = 0, 1, 2, 3, …

2x – 3 ≤ 1
2x ≤ 4
x ≤ 2
x = 2, 1, 0, –1, …

Therefore x = 0, 1, 2

Question 8:

Given that 3 < \sqrt{x - 2} < 4 and x is an integer . List all the possible values of x .

Solution:

\begin{array}{l} 3 < \sqrt{x - 2} < 4 \\ 3^{2} < x - 2 < 4^{2} \\ 9 < x - 2 \\ x > 11 \\ or x - 2 < 16 \\ x < 18 \\ 11 < x < 18 \\ x = 12, 13, 14, 15, 16, 17 \end{array}

Question 9:
Find the biggest and the smallest integer of x that satisfy
3x + 2 ≥ –4 and 4 – x > 0.

Solution:
3x + 2 ≥ –4
3x ≥ –4 – 2
3x ≥ –6
x ≥ –2

4 – x > 0
–x > –4
x < 4

Smallest integer of x is –2, and the biggest integer of x is 3.

Question 10:

\begin{array}{l} If x \leq h \leq y satisfy the two inequalities 7 - \frac{h}{2} \leq 5 and \\ 3 (h + 2) \leq 20 + h, find the values of x and y . \end{array}

Solution:

\begin{array}{l} 7 - \frac{h}{2} \leq 5 \\ - \frac{h}{2} \leq 5 - 7 \\ - h \leq - 4 \\ h \geq 4 \\ 3 (h + 2) \leq 20 + h \\ 3 h + 6 \leq 20 + h \\ 2 h \leq 14 \\ h \leq 7 \\ 4 \leq h \leq 7 \\ ∴ x = 4, y = 7 \end{array}

12.2.1 Linear Inequalities, PT3 Focus Practice

Posted on May 18, 2018 by user

12.2.1 Linear Inequalities, PT3 Focus Practice

Question 1:

Draw a number line to represent the solution for the linear inequalities –3 < 5 – x ≤ 4.

Solution:

–3 < 5 – x and 5 – x ≤ 4

x < 5 + 3 and –x ≤ 4 – 5

x < 8 and –x ≤ –1 → x ≥ 1

Thus, the solution is 1 ≤ x < 8

Question 2:

Solve the following simultaneous linear inequalities.

3 x - 5 \leq 1 and 2 - \frac{1}{3} x < 3

Solution:

3x – 5 ≤ 1

3x ≤ 1 + 5

3x ≤ 6

x ≤ 2

\begin{array}{l} 2 - \frac{1}{3} x < 3 \\ 6 - x < 9 \leftarrow Multiply by 3 \\ - x < 9 - 6 \\ - x < 3 \\ x > - 3 \leftarrow Multiply by - 1 \end{array}

The solution is –3 < x ≤ 2.

Question 3:

The solution for the inequality 2 + x < 3x – 4 is

Solution:

2 + x < 3x – 4

x – 3x < –4 – 2

–2x < –6

–x < –3

x > 3

Question 4:

The solution for the inequality –2 (6y + 3) < 3 (4 – 2y) is

Solution:

–2 (6y + 3) < 3 (4 – 2y)

–12y – 6 < 12 – 6y

–12y + 6y < 12 + 6

–6y < 18

–y < 3

y > –3

Question 5:

Solve each of the following inequalities.

(a) 3x + 4 > 5x – 10

(b) –3 ≤ 2x + 1 < 7

Solution:

(a)

3x + 4 > 5x – 10

3x – 5x > –10 – 4

–2x > –14

–x > –7

x < 7

(b)

–3 ≤ 2x + 1 < 7

–3 ≤ 2x + 1 and 2x + 1 < 7

–2x ≤ 1 + 3 and 2x < 7 – 1

–2x ≤ 4 and 2x < 6

x ≥ –2 and x < 3

The solution is –2 ≤ x < 3.

12.1 Linear Inequalities

Posted on May 15, 2018 by user

12.1 Linear Inequalities

12.1.1 Inequalities

1. To write the relationship between two quantities which are not equal, we use the following inequality signs:

> greater than

< less than

≥ greater than or equal to

≤ less than or equal to

2. 7 > 4 also means 4 < 7. 7 > 4 and 4 < 7 are equivalent inequalities.

12.1.2 Linear Inequalities in One Unknown

1. An inequality in one unknown to the power of 1 is called a linear inequality.

Example: 2x + 5 > 7

2. A linear inequality can be represented on a number line.

Example:

12.1.3 Computation on Inequalities

1. When a number is added or subtracted from both sides of an inequality, the condition of the inequality is unchanged.

Example:

Given 5 > 3

Then, 5 + 2 > 3 + 2 ← (symbol ‘>’ remains)

Hence, 7 > 5

2. When both sides of an inequality are multiplied or divided by the same positive number, the condition of the inequality is unchanged.

Example:

Given 4x ≤ 16

Then, 4x ÷ 4 ≤ 16 ÷ 4 ← (symbol ‘≤’ remains)

Hence, x ≤ 4

3. When both sides of an inequality are multiplied or divided by the same negative number, the inequality is reversed.

Example:

Given –3 > –5

Hence, 3 < 5

Given –5y > –10

Then, –5y ÷ 5 > –10 ÷ 5

–y > –2

Hence, y < 2

12.1.4 Solve Inequalities in One Variable

To solve linear inequalities in one variable, use inverse operation to make the variable as the subject of the inequality.

Example:

Solve the following linear inequalities.

\begin{array}{l} (a) 3 - 2 x < 1 \\ (b) \frac{5 - 2 x}{3} \leq 7 \end{array}

Solution:

(a)

\begin{array}{l} 3 - 2 x < 1 \\ 3 - 2 x - 3 < 1 - 3 \\ - 2 x < - 2 \\ 2 x > 2 \\ \frac{2 x}{2} > \frac{2}{2} \\ x > 1 \end{array}

(b)

\begin{array}{l} \frac{5 - 2 x}{3} \leq 7 \\ (\frac{5 - 2 x}{3}) \times 3 \leq 7 \times 3 \\ 5 - 2 x \leq 21 \\ - 2 x \leq 16 \\ 2 x \geq - 16 \\ \frac{2 x}{2} \geq - \frac{16}{2} \\ x \geq - 8 \end{array}

12.1.5 Simultaneous Linear Inequalities in One Variable

1. The common values of two simultaneous inequalities are values which satisfy both linear inequalities.

The common values of the simultaneous linear inequalities x ≤ 3 and x > –1 is –1 < x ≤ 3.

2. To solve two simultaneous linear inequalities is to find a single equivalent inequality which satisfies both inequalities.

11.2.2 Linear Equations II, PT3 Focus Practice

Posted on May 6, 2018 by user

Question 6:
Diagram below shows 5 boxes of orange juice and 2 bottles of milk. Both orange juice and milk are mixed to produce 18 litres drink.

(a) Based on the above situation, write a linear equation.
(b) If 9 litres of drinks is produced by using 2 boxes of orange juice and 2 bottles of milk, find the volume, in litre, of orange juice in each box.

Solution:
Let j be the number of boxes of orange juice and m be the number of bottles of milk.
(a)
5j + 2m = 18

(b)

\begin{array}{l} 2 j + 2 m = 9 ............. (1) \\ 5 j + 2 m = 18 ............. (2) \\ (2) - (1) : \\ 3 j = 9 \\ j = \frac{9}{3} = 3 \\ 3 litres of orange juice in each box . \end{array}

11.2.1 Linear Equations II, PT3 Focus Practice

Posted on May 5, 2018 by user

11.2.1 Linear Equations II, PT3 Focus Practice

Question 1:

It is given that 2x = 6 and 3x + y = 10.

Calculate the value of y.

Solution:

2x = 6

x = 3

Substitute x = 3 into 3x + y = 10

3 (3) + y = 10

y = 10 – 9

y = 1

Question 2:

It is given that y = –1 and x – 3y = –10.

Calculate the value of x.

Solution:

Substitute y = –1 into x – 3y = –10

x – 3 (–1) = –10

x + 3 = –10

x = –10 – 3

x = –13

Question 3:

It is given that 7x – 2y = 19 and x + y = 13.

Calculate the value of y.

Solution:

Using Substitution method

7x – 2y = 19 -------- (1)

x + y = 13 ------- (2)

From equation (2),

x = 13 – y ------- (3)

Substitute equation (3) into equation (1),

7x – 2y = 19

7 (13 – y) – 2y = 19

91 – 7y – 2y = 19

– 9y = 19 – 91

– 9y = –72

y = 8

Question 4:

It is given that 2x – y = 5 and 3x – 2y = 8.

Calculate the value of x.

Solution:

Using Elimination method

2x – y = 5 -------- (1)

3x – 2y = 8 ------- (2)

(1) × 2: 4x – 2y = 10 -------- (3)

3x – 2y = 8 ------- (2)

(3) – (2): x – 0 = 2

x = 2

Question 5:

It is given that x + 2y = 4 and x + 6y = –4.

Calculate the value of x.

Solution:

Using Elimination method

x + 2y = 4 -------- (1)

x + 6y = –4 ------- (2)

(1) × 3: 3x + 6y = 12 -------- (3)

x + 6y = –4 ------- (2)

(3) – (2): 2x = 12 – (–4)

2x = 16

x = 8

11.1 Linear Equations II

Posted on May 1, 2018 by user

11.1 Linear Equations II

11.1.1 Linear Equations in Two Variables

1. A linear equation in two variables is an equation which contains only linear terms and involves two variables.

2. If the value of one variable in an equation is known, then the value of the other variable can be determined and vice versa.

Example:

Given that 2x + 3y = 6, find the value of

(a) x when y = 4, (b) y when x = –3

Solution:

(a) Substitute y = 4 into the equation.

2x + 3y = 6

2x + 3 (4) = 6

2x + 12 = 6

2x = 6 – 12

2x = –6

x = –3

(b) Substitute x = –3 into the equation.

2x + 3y = 6

2 (–3) + 3y = 6

–6 + 3y = 6

3y = 6 + 6

3y = 12

y = 4

3. A linear equation in two variables has many possible solutions.

11.1.2 Simultaneous Linear Equations in Two Variables

1. Two equations are said to be simultaneous linear equations in two variables if

(a) Both are linear equations in two variables, and

(b) Both involve the same variables.

Example: 2x + y = 9, x = 2y + 1

2. The solution of two simultaneous linear equations in two variables is any pair of values (x, y) that satisfied both the equations.

3. Simultaneous linear equations in two variables can be solved by the substitution method or the elimination method.

Example:

Solve the following simultaneous linear equation.

2x + y = 9

3x – y = –4

Solution:

(A) Substitution method

2x + y = 9 -------- (1) ← label the equations as (1) and (2)

3x – y = –4 ------- (2)

From equation (1),

y = 9 – 2x ------- (3) ← expressing y in terms of x.

Substitute equation (3) into equation (2),

3x – (9 – 2x) = –4

3x – 9 + 2x = –4

5x = –4 + 9

5x = 5

x = 1

Substitute x = 1 into equation (1),

2 (1) + y = 9

2 + y = 9

y = 9 – 2

y = 7

The solution is x = 1, y = 7.

(B) Elimination method

2x + y = 9 -------- (1) ← Both equations have the same coefficient of y.

3x – y = –4 ------- (2)

(1) + (2): 2x + 3x = 9 + (–4) ← y + (–y) = 0

5x = 5

x = 1

Substitute x = 1 into equation (1) or (2),

2x + y = 9 -------- (1)

2 (1) + y = 9

y = 9 – 2

y = 7

The solution is x = 1, y = 7.

10.2.2 Transformations II, PT3 Focus Practice

Posted on April 21, 2018 by user

Question 6:
Diagram below shows a ‘Wayang Kulit’ performed by Tok Dalang. The height of the screen use is 1.5 m. The shadow on the screen is ⅔ the height of the screen.

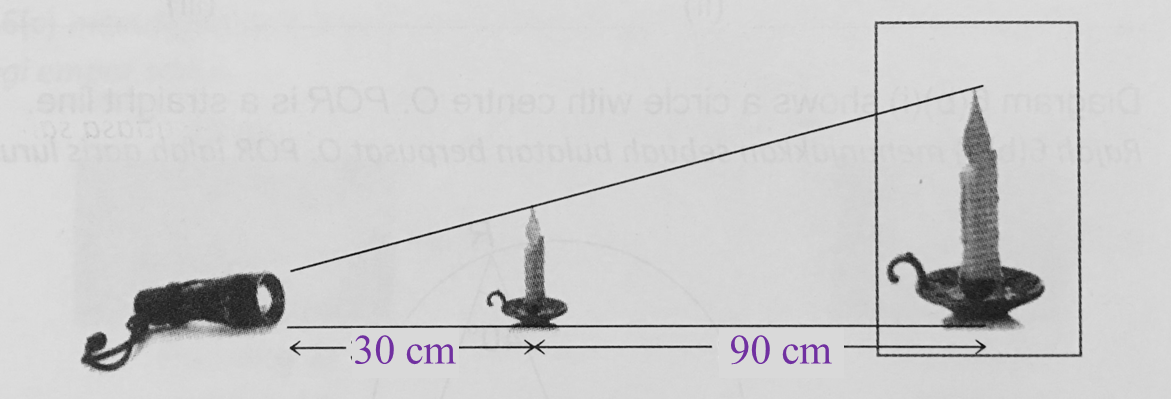
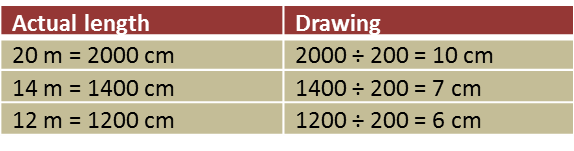
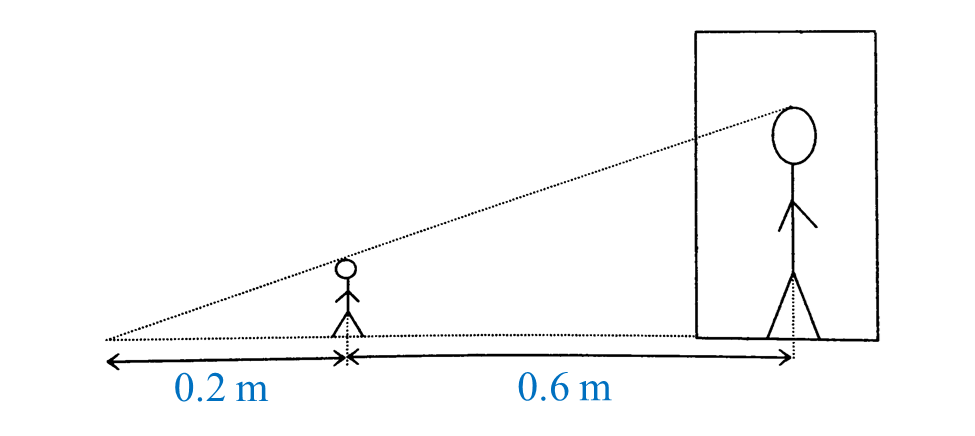What is the height, in cm, of the puppet used by Tok Dalang?

Solution:

\begin{array}{l} Height of shadow \\ = \frac{2}{3} of height of screen \\ = \frac{2}{3} \times 1.5 m \\ = 1.0 m \\ \frac{Height of puppet}{Height of shadow} = \frac{0.2}{0.2 + 0.6} \\ \frac{Height of puppet}{1} = \frac{0.2}{0.8} \\ Height of puppet \\ = 0.25 m \\ = 25 cm \end{array}

Question 7:
Diagram below shows the shadow of a pillar form on the wall from the light of a spotlight.

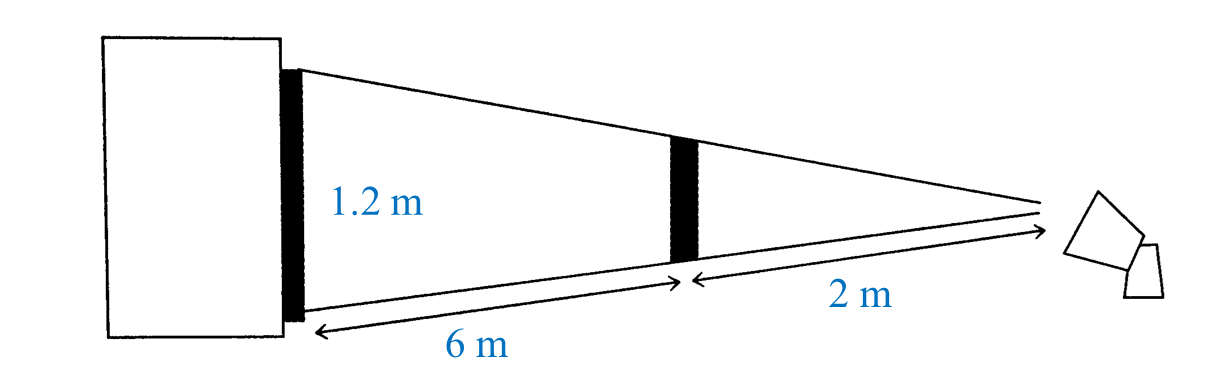(a) State the scale factor of the enlargement.
(b) Find the height of the pillar.

Solution:
(a)

\begin{array}{l} Scale factor = \frac{2 + 6}{2} \\ = \frac{8}{2} \\ = 4 \end{array}

(b)

\begin{array}{l} \frac{Height of pillar}{Height of shadow} = \frac{1}{4} \\ \frac{Height of pillar}{1.2} = \frac{1}{4} \\ Height of pillar = \frac{1}{4} \times 1.2 m \\ = 0.3 m \end{array}

Question 8:
In diagram below, a torch light is used to form a shadow of a candle on the screen.

The height of the candle is 15 cm.
If the height of the shadow of the candle is ¾ of the height of the screen, find the height of the screen.

Solution:

\begin{array}{l} \frac{Height of candle}{Height of shadow} = \frac{30}{30 + 90} \\ \frac{15 cm}{Height of shadow} = \frac{1}{4} \\ Height of shadow = 15 cm \times 4 \\ = 60 cm \\ \frac{3}{4} of height of screen = 60 cm \\ Height of screen = \frac{4}{3} \times 60 cm \\ = 80 cm \end{array}

10.2.1 Transformations II, PT3 Focus Practice

Posted on April 19, 2018 by user

10.2.1 Transformations II, PT3 Focus Practice

Question 1:

In the diagram, ∆P’Q’R’ is the image of ∆PQR under an enlargement.

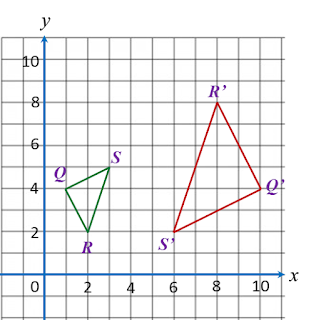
(a) State the scale factor of the enlargement.

(b) If the area of ∆PQR = 7 cm², calculate the area of ∆P’Q’R’.

Solution:

(a)

Scale factor, k = \frac{P' Q'}{P Q} = \frac{6}{3} = 2

(b)

Area of image = k²× Area of object

Area of ∆P’Q’R’ = 2²× 7

= 28 cm²

Question 2:

In diagram below, OP’Q’ is the image of OPQ under an enlargement with centre O.

Given PQ = 4cm, calculate the length, in cm, of P’Q’.

Solution:

\begin{array}{l} \frac{P' Q'}{P Q} = \frac{O P'}{O P} \\ \frac{P' Q'}{4} = \frac{9}{3} \\ P' Q' = \frac{9}{3} \times 4 \\ = 12 cm \end{array}

Question 3:

In diagram below, PQ’R’S’ is the image of PQRS under an enlargement.

Calculate the length, in cm, of SS’.

Solution:

\begin{array}{l} \frac{P S}{P S'} = \frac{P Q}{P Q'} \\ \frac{P S}{36} = \frac{4}{16} \\ P S = \frac{4}{16} \times 36 \\ = 9 cm \\ S S' = 36 - 9 \\ = 27 cm \end{array}

Question 4:

On the Cartesian plane, Q’R’S’ is the image of ∆ QRS under an enlargement of centre T.

State the coordinates of T.

Solution:

Coordinates of T = (4, 4).

Question 5:

In diagram below, quadrilateral AFGH is the image of ABCD under an enlargement.

(a) Find the scale factor of the enlargement.

(b) The area represented by the quadrilateral AFGH is 15cm². Find the area, in cm², represented by the shaded region.

Solution:

(a)

\begin{array}{l} Scale factor \\ = \frac{3}{6 + 3} = \frac{3}{9} = \frac{1}{3} \end{array}

(b)

Area of image = k²× Area of object

\begin{array}{l} 15 = {(\frac{1}{3})}^{2} \times Area of object \\ Area of object = 15 \times 9 = 135 \\ Area of shaded region = 135 - 15 \\ = 120 c m^{2} \end{array}

10.1 Transformations II

Posted on April 16, 2018 by user

10.1 Transformations II

10.1.1 Similarity

Two shapes are similar if

(a) the corresponding angles are equal and

(b) the corresponding sides are proportional.

Example:

Quadrilateral ABCD is similar to quadrilateral JKLM because

\begin{array}{l} ∠ A = ∠ J = 90^{o} \\ ∠ B = ∠ K = 50^{o} \\ ∠ C = ∠ L = 130^{o} \\ ∠ D = ∠ M = 90^{o} \end{array}

(All the corresponding angles are equal.)

\begin{array}{l} \frac{A B}{J K} = \frac{5}{10} = \frac{1}{2} \\ \frac{B C}{K L} = \frac{4}{8} = \frac{1}{2} \\ \frac{C D}{L M} = \frac{2.5}{5} = \frac{1}{2} \\ \frac{A D}{J M} = \frac{3}{6} = \frac{1}{2} \end{array}

(All the corresponding sides are proportional.)

10.1.2 Enlargement

1. Enlargement is a type of transformation where all the points of an object move from a fixed point at a constant ratio.

2. The fixed point is known as the centre of enlargement and the constant ratio is known as the scale factor.

Scale factor = \frac{length of side of image}{length of side of object}

3. The object and the image are similar.

4. If A’ is the image of A under an enlargement with centre O and scale factor k, then

\frac{O A'}{O A} = k

if k > 0, then the image is on the same side of the object.
if k < 0, then the image is on the opposite side of the object.
if –1 < k < 1, then the size of the image is a reduction of the size of the object.

5. Area of image = k² × area of object.

9.2.2 Scale Drawings, PT3 Focus Practice

Posted on April 3, 2018 by user

Question 6:
Diagram below shows an irregular pentagon.

By using the scale 1 : 200, complete the scale drawing in the answer space provided. The grid has equal square with sides of 1 cm.

Answer:

Solution:

Question 7:
Diagram below shows polygon.

(a) If the polygon is redrawn using the scale 1 : 500, calculate the length of side drawn for the side 15 m.
(b) On the square grids in the answer space, redraw the polygon using the scale 1 : 500. The grid has equal squares with sides of 1 cm.

Answer:

\begin{array}{l} (a) \\ Length of side of the drawing \\ = \frac{15}{5} \\ = 3 cm \end{array}

(b)