Question 1:
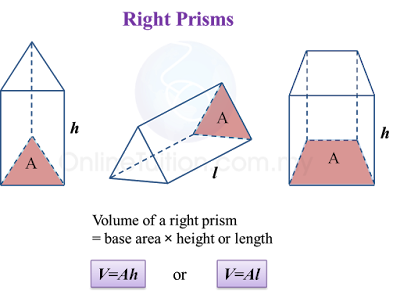
Diagram below shows polygon P drawn on a grid of equal squares with sides of 1 unit.
On the grid in the answer space, redraw polygon P using the scale 1 : 12.
The grid has equal squares with sides of 1 unit.
Answer:
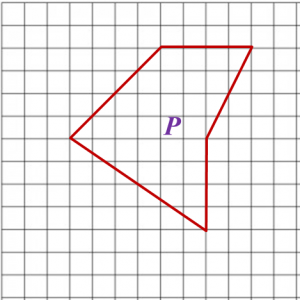
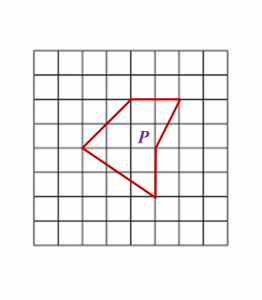
Diagram below shows polygon P drawn on a grid of equal squares with sides of 1 unit.

On the grid in the answer space, redraw polygon P using the scale 1 : 12.
The grid has equal squares with sides of 1 unit.
Answer:

Question 2:
Diagram below shows polygon W drawn on a grid of equal squares with sides of 1 unit.
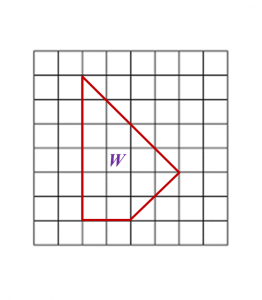
On the grid in the answer space, redraw polygon W using the scale 1 : 2.
The grid has equal squares with sides of 1 unit.
Answer:
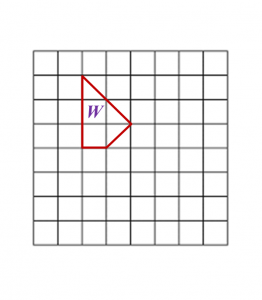
Diagram below shows polygon W drawn on a grid of equal squares with sides of 1 unit.

On the grid in the answer space, redraw polygon W using the scale 1 : 2.
The grid has equal squares with sides of 1 unit.
Answer:

Question 3:
Diagram below shows a polygon PQRSTU.

(a) If the polygon is redrawn using the scale 1 : 400, calculate the length of PQ.
(b) In the answer space, redraw the polygon using the scale 1 : 400. The grid has equal squares with sides of 1 cm.
Answer:
(a)
Length of PQ=4800 cm400 =12 cm
(b)
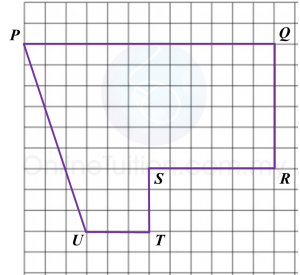
Diagram below shows a polygon PQRSTU.

(a) If the polygon is redrawn using the scale 1 : 400, calculate the length of PQ.
(b) In the answer space, redraw the polygon using the scale 1 : 400. The grid has equal squares with sides of 1 cm.
Answer:
(a)
Length of PQ=4800 cm400 =12 cm
(b)

Question 4:
Diagram below shows a polygon.

On the grid in the answer space, redraw the polygon using the scale 1 : 500. The grid has equal squares with sides of 1 cm.
Answer:
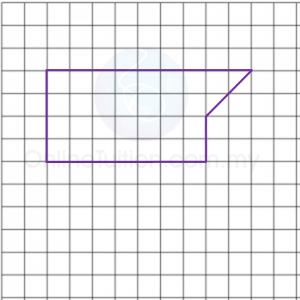
Diagram below shows a polygon.

On the grid in the answer space, redraw the polygon using the scale 1 : 500. The grid has equal squares with sides of 1 cm.
Answer:
| Actual length | Drawing |
| 45 m = 4500 cm | 4500 ÷ 500 = 9 cm |
| 20 m = 2000 cm | 2000 ÷ 500 = 4 cm |
| 35 m = 3500 cm | 3500 ÷ 500 = 7 cm |
| 10 m = 1000 cm | 1000 ÷ 500 = 2 cm |

Question 5:
Diagram below shows a polygon.

(a) If the polygon is redrawn using the scale 1 : 300, calculate the length, in cm, the drawing for the side 24 m.
(b) In the answer space, redraw the polygon using the scale 1 : 300. The grid has equal squares with sides of 1 cm.
Answer:
(a)
Length of side of the drawing=2400 cm300=8 cm
(b)
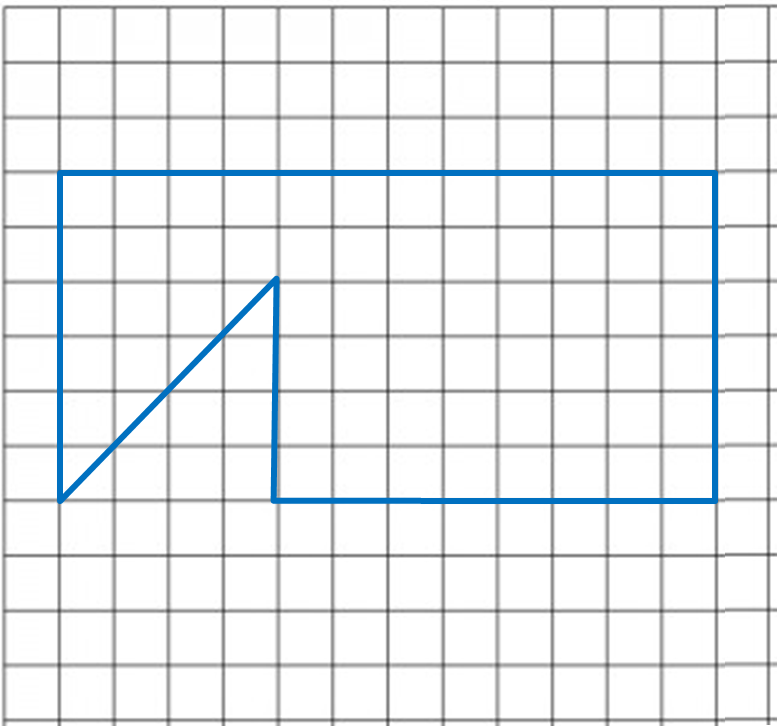
Diagram below shows a polygon.

(a) If the polygon is redrawn using the scale 1 : 300, calculate the length, in cm, the drawing for the side 24 m.
(b) In the answer space, redraw the polygon using the scale 1 : 300. The grid has equal squares with sides of 1 cm.
Answer:
(a)
Length of side of the drawing=2400 cm300=8 cm
(b)


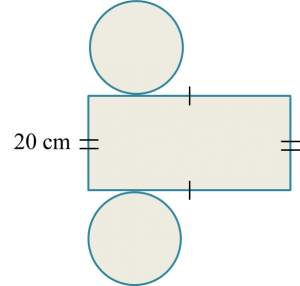
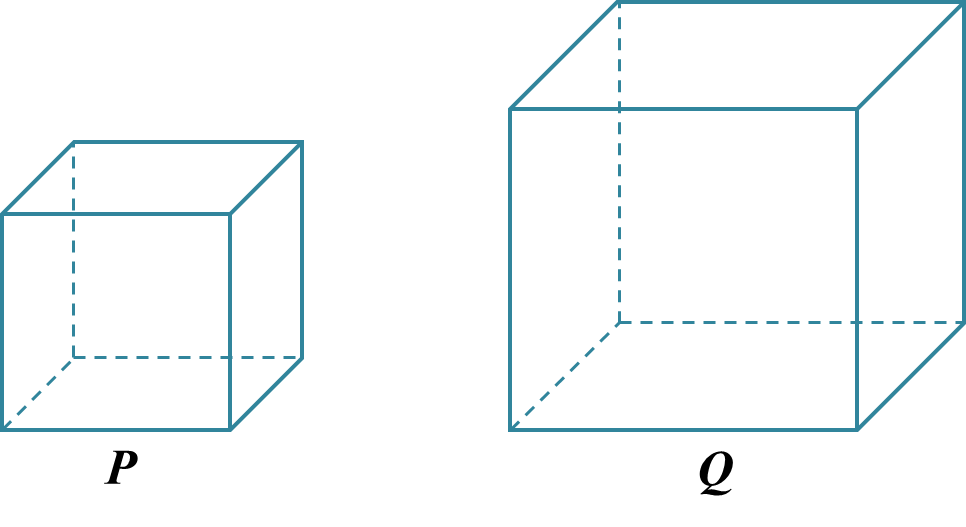 Find the difference in volume between cube P and cube Q.
Find the difference in volume between cube P and cube Q.