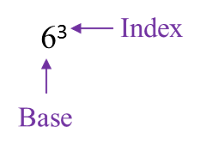
6.1 Algebraic Expressions III
6.1.1 Expansion
1. The product of an algebraic term and an algebraic expression:
- a(b + c) = ab + ac
- a(b – c) = ab – ac
2. The product of an algebraic expression and another algebraic expression:
- (a + b) (c + d) = ac + ad + bc + bd
- (a + b)2= a2 + 2ab + b2
- (a – b)2= a2 – 2ab + b2
- (a + b) (a – b) = a2 – b2
6.1.2 Factorization
1. Factorize algebraic expressions:
- ab + ac = a(b + c)
- a2– b2 = (a + b) (a – b)
- a2+ 2ab + b2 = (a + b)2
- ac + ad + bc + bd = (a + b) (c + d)
2. Algebraic fractions are fractions where both the numerator and the denominator or either the numerator or the denominator are algebraic terms or algebraic expressions.
Example:
3b,a7,a+ba,ba−b,a−bc+d
3(a) Simplification of algebraic fractions by using common factors:
•14bc312bd=c3d•bm+bnem+en=b(m+n)e(m+n)=be
3(b) Simplification of algebraic fractions by using difference of two squares:
a2−b2an+bn=(a+b)(a−b)n(a+b)=a−bn
6.1.3 Addition and Subtraction of Algebraic Fractions
1. If they have a common denominator:
am+bm=a+bm
2. If they do not have a common denominator:
6.1.4 Multiplication and Division of Algebraic Fractions
1. Without simplification:
•am×bn=abmn•am÷bn=am×nb=anbm
2. With simplification:
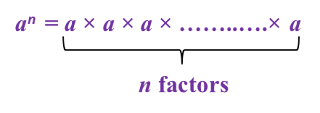
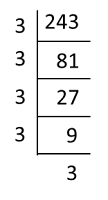
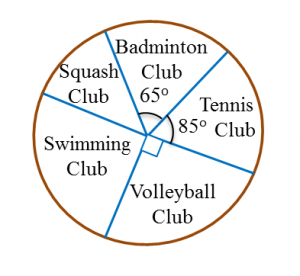
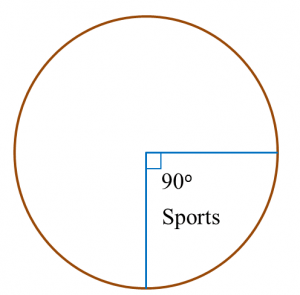

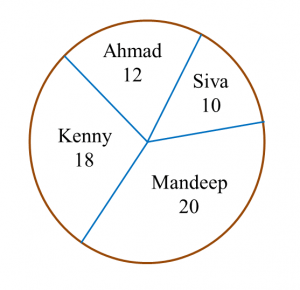

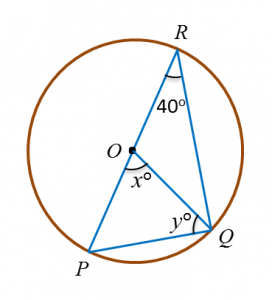
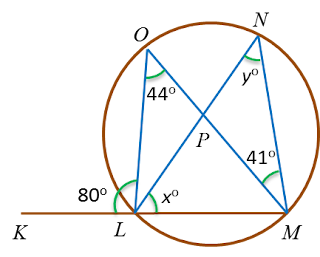
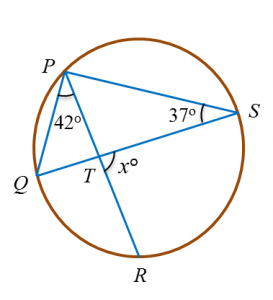 Find the value of x.
Find the value of x.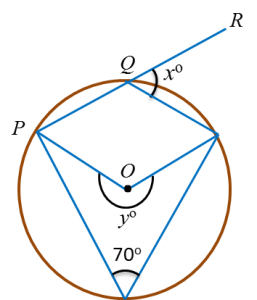
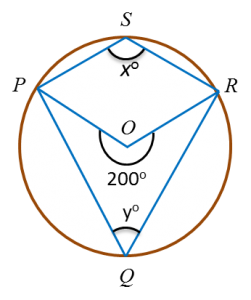
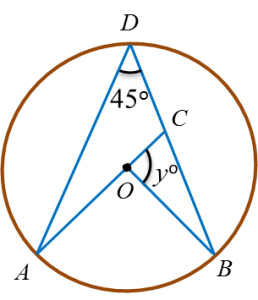
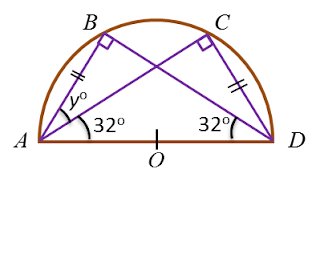
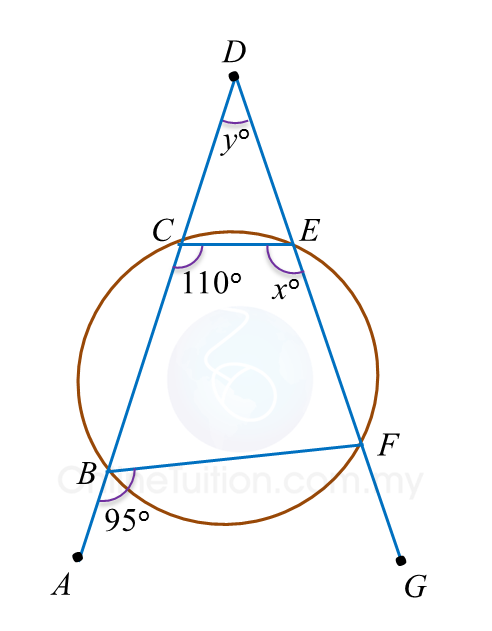 Find the value of x and of y.
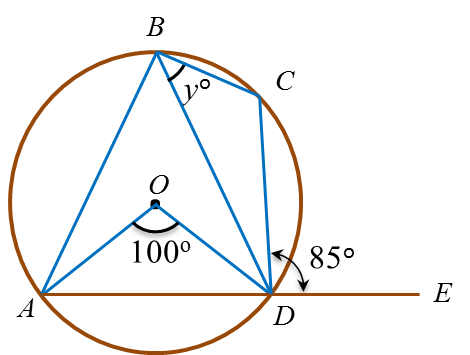
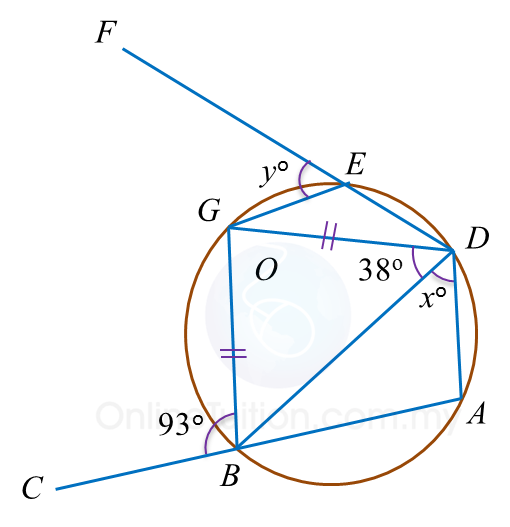
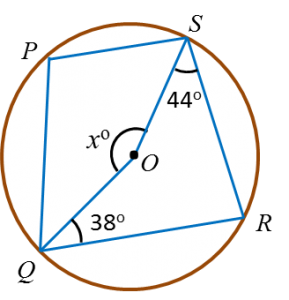
Find the value of x and of y.