PT3 Maths
2.2.2 Polygons II, PT3 Practice
Question 6:
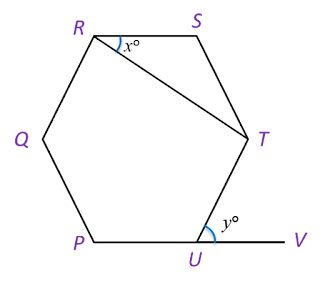
In diagram below, PQRSTU is a regular hexagon QUV is a straight line.
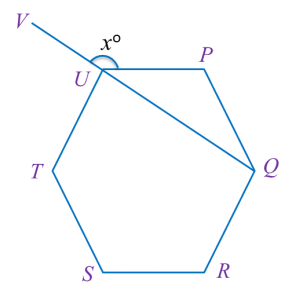
Find the value of x.
Solution:
Each interior angle=(6−2)×180o6=120o∠PUQ=180o−120o2=30o (△PUQ is a isosceles triangle)xo=180o−30o=150ox=150
In diagram below, PQRSTU is a regular hexagon QUV is a straight line.

Find the value of x.
Solution:
Each interior angle=(6−2)×180o6=120o∠PUQ=180o−120o2=30o (△PUQ is a isosceles triangle)xo=180o−30o=150ox=150
Question 7:
In diagram below, PQRSTU is a hexagon. UPE, PQF, QRG, RSH and UTJ are straight lines.
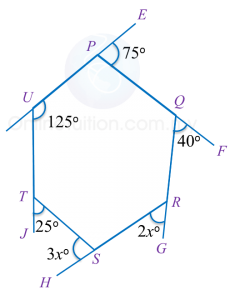
Find the value of x.
Solution:
Sum of all the exterior angles of any polygon=360o25o+3xo+2xo+40o+75o+55o=360o5xo+195o=360o 5xo=360o−195o =165oxo=165o÷5 =33o x=33
In diagram below, PQRSTU is a hexagon. UPE, PQF, QRG, RSH and UTJ are straight lines.

Find the value of x.
Solution:
Sum of all the exterior angles of any polygon=360o25o+3xo+2xo+40o+75o+55o=360o5xo+195o=360o 5xo=360o−195o =165oxo=165o÷5 =33o x=33
Question 8:
In Diagram below, A, B, C, D and E are vertices of a 9 sided regular polygon.
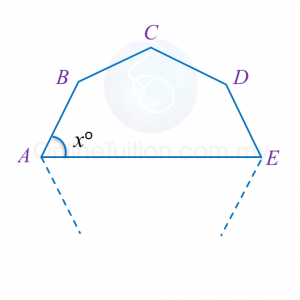
Find the value of x.
Solution:
Exterior angle =360o9=40oInterior angle=180o−40o=140oSum of interior angles of pentagon ABCDE=(5−2)×180o=540oxo+140o+140o+140o+xo=540o2xo=540o−420o =120o xo=60o x=60
In Diagram below, A, B, C, D and E are vertices of a 9 sided regular polygon.

Find the value of x.
Solution:
Exterior angle =360o9=40oInterior angle=180o−40o=140oSum of interior angles of pentagon ABCDE=(5−2)×180o=540oxo+140o+140o+140o+xo=540o2xo=540o−420o =120o xo=60o x=60
2.2.1 Polygons II, PT3 Practice
2.2.1 Polygons II, PT3 Practice
Question 1:
Diagram below shows a pentagon PQRST. TPU and RSV are straight lines.
Find the value of x.
Solution:
Sum of interior angles of a pentagon=(5−2)×180o=3×180o=540o∠TSR=180o−70o =110o∠TPQ=180o−85o =95oxo=540o−(110o+105o+115o+95o) =540o−425o =115o x=115
Question 2:
In Diagram below, PQRSTU is a hexagon. APQ and BTS are straight lines.Solution:
∠QPU=180o−160o=20oReflex∠PUT=360o−80o=280o∠UTS=180o−120o=60o∠TSR=180o−35o=145oSum of interior angles of a hexagon=(6−2)×180o=720oxo+yo+145o+60o+280o+20o=720oxo+yo=720o−505o=215ox+y=215
Question 3:
Diagram below shows a regular hexagon PQRSTU. PUV is a straight line.Find the value of x + y.
Solution:
Size of each interior angle of a regular hexagon=(6−2)×180o6=120oxo=180o−120o2=30oyo=180o−120o=60oxo+yo=30o+60o=90ox+y=90
Question 4:
In the diagram below, KLMNP is a regular pentagon. LKS and MNQ are straight lines.Solution:
Size of each interior angle of a regular pentagon=(5−2)×180o5=108o∠PKS=∠PNQ=180o−108o=72oReflex angle∠KPN=360o−108o=252o
Sum of interior angles of a hexagon=(6−2)×180o=720o∴
2.1 Polygons II
2.1 Polygons II
2.1.1 Regular Polygons
1. A regular polygon is a polygon where
(a) all its sides are of equal length, and
(b) all its interior angles are of equal size.
2. The number of axis of symmetry of a regular polygon is equal to its number of sides.
Example:
2.1.2 Exterior and Interior Angles of Polygons
1. The exterior and interior angles at a vertex of a polygon is supplementary.
2. The sum of interior angles of an n-sided polygon is
3. Each interior angle of a regular n-sided polygon is
4. The sum of all exterior angles of a polygon is 360o.
5. Each exterior angle of a regular n-sided polygon is
1.2.1 Angles and Lines II, PT3 Practice
1.2.1 Angles and Lines II, PT3 Practice
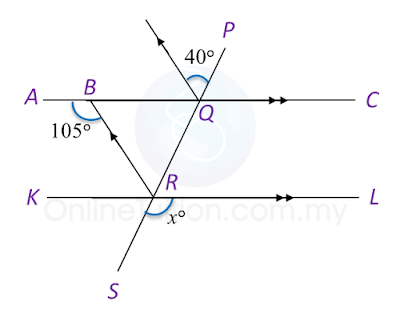
Question 1:
Find the value of x.
Question 2:
(a) In Diagram below, PQR and SQT are straight lines.Find the value of x.
(b) In Diagram below, PQRS is a straight line. Find the value of x.
Solution:
(a)
(b)
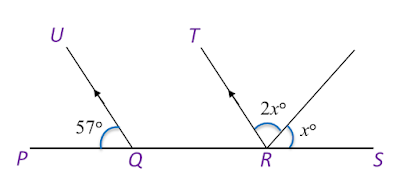
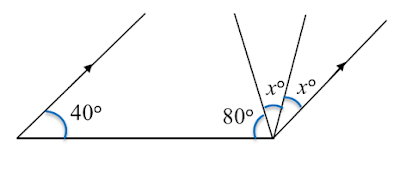
Question 4:
Solution:
40o + 80o + xo + xo = 180o
2xo = 180o – 120o
2xo = 60o
xo = 30o
x = 30
1.1 Angles and Lines II
1.1 Angles and Lines II
Identifying Parallel, Transversals, Corresponding Angles, Alternate Angles and Interior Angles
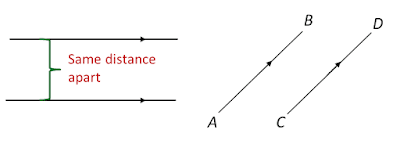
(A) Parallel lines
Parallel lines are lines with the same direction. They remain the same distance apart and never meet.
(B) Transversal lines
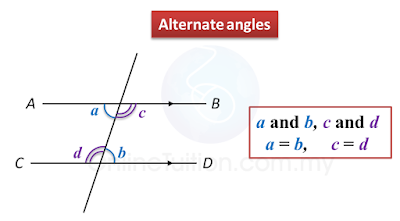
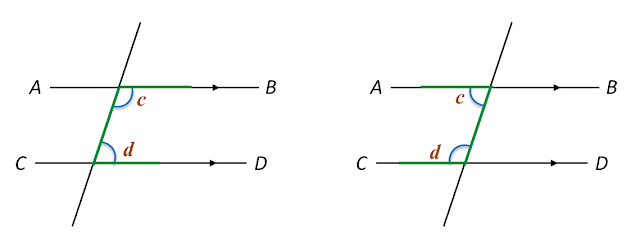
(C) Alternate angles
(D) Corresponding angles
(E) Interior angles
PT3 Smart TIP
Alternate angles are easily identified by tracing out the pattern “Z” as shown.
Corresponding angles are easily identified by the pattern “F” as shown.

Interior angles are easily identified by the pattern “C” as shown.
Example 1:
Construct a line parallel to PQ and passing through W.
a = 40o and b = 50o← (Alternate angles)
y = a + b
= 40o+ 50o
= 90o
13.2.3 Statistics (I), PT3 Focus Practice
Question 7:
Diagram below is an incomplete pictograph showing the sales of books for a duration of five months.
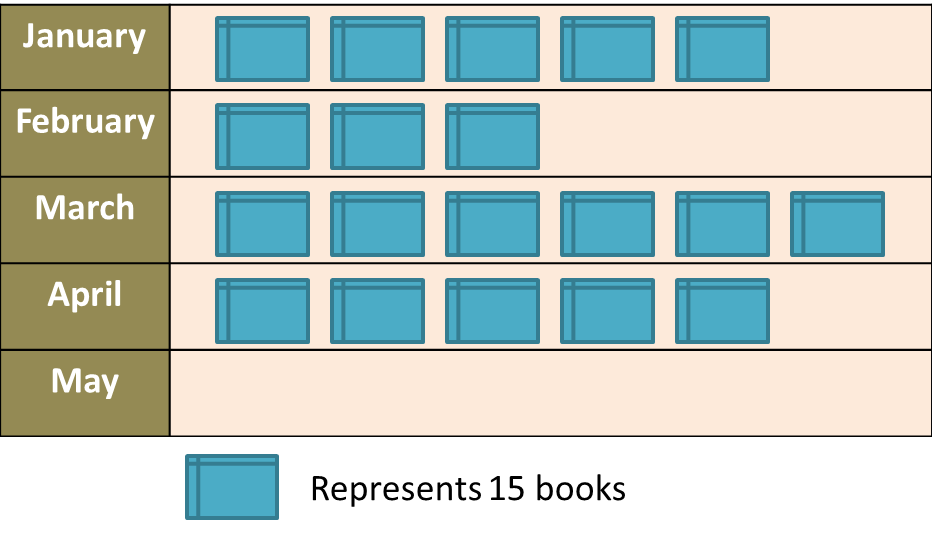
(a) The sales in May is ¼ of the total sales in January and February.
Complete the pictograph in the Diagram.
(b) Find the total number of books sold before April.
Solution:
(a)
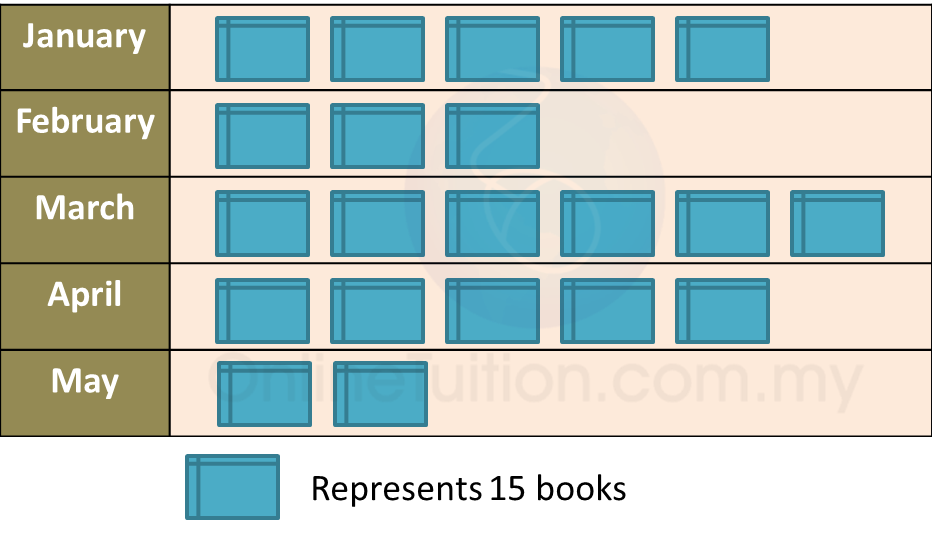
(b)
Total number of books sold before April
= (5 + 3 + 6) × 15
= 14 × 15
= 210
Diagram below is an incomplete pictograph showing the sales of books for a duration of five months.

(a) The sales in May is ¼ of the total sales in January and February.
Complete the pictograph in the Diagram.
(b) Find the total number of books sold before April.
Solution:
(a)

(b)
Total number of books sold before April
= (5 + 3 + 6) × 15
= 14 × 15
= 210
Question 8:
Diagram below shows an incomplete line graph of the number of eggs sold in four weeks. The number of eggs sold on week 1 is 2000 and 4000 on week 4.
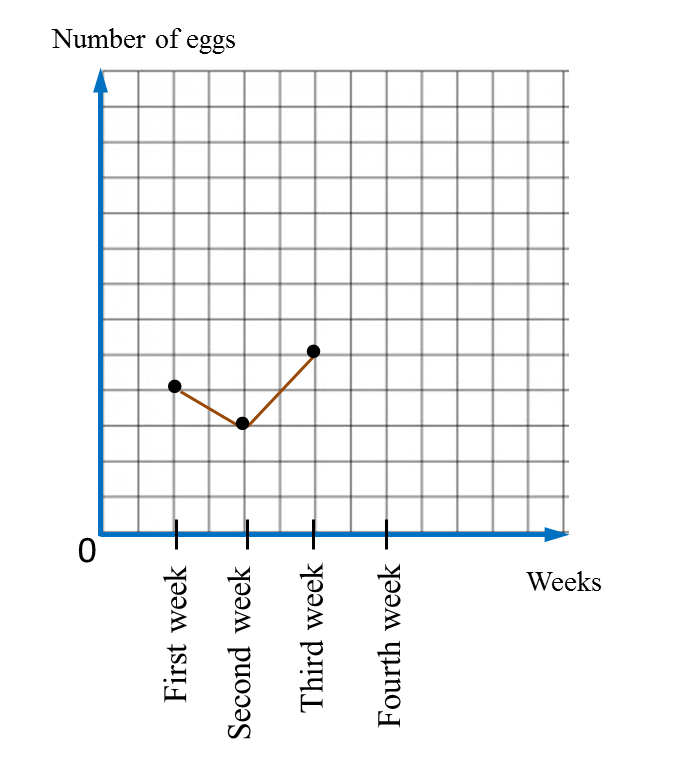
(a) Complete the line graph in the Diagram.
(b) Complete the pie chart in the second Diagram to represent sales from Week 1 to Week 4.

Solution:
(a)
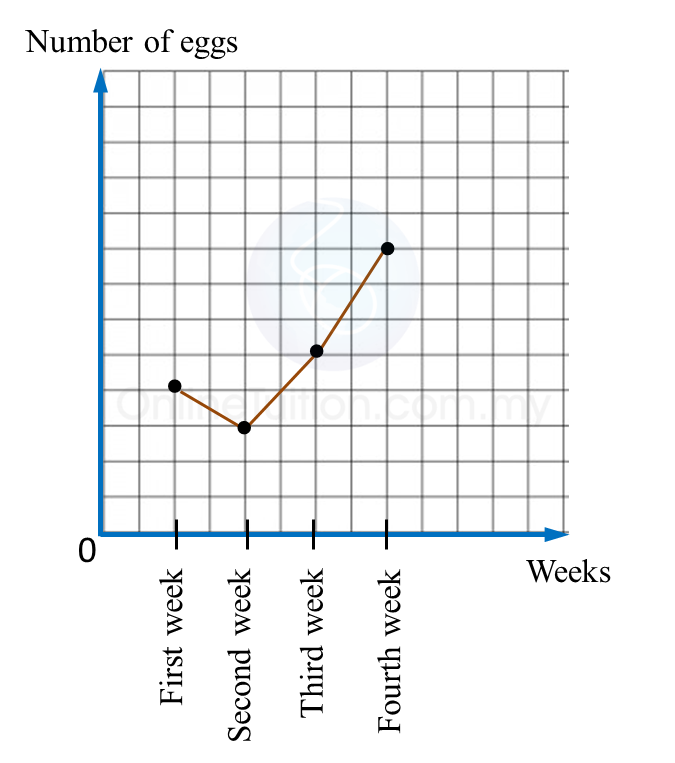
(b)
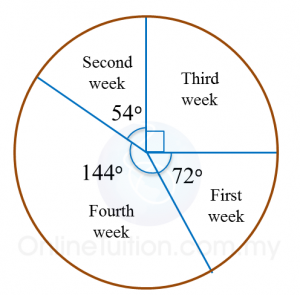
Diagram below shows an incomplete line graph of the number of eggs sold in four weeks. The number of eggs sold on week 1 is 2000 and 4000 on week 4.

(a) Complete the line graph in the Diagram.
(b) Complete the pie chart in the second Diagram to represent sales from Week 1 to Week 4.

Solution:
(a)

(b)

13.2.2 Statistics (I), PT3 Focus Practice
13.2.2 Statistics (I), PT3 Focus Practice
Question 4:
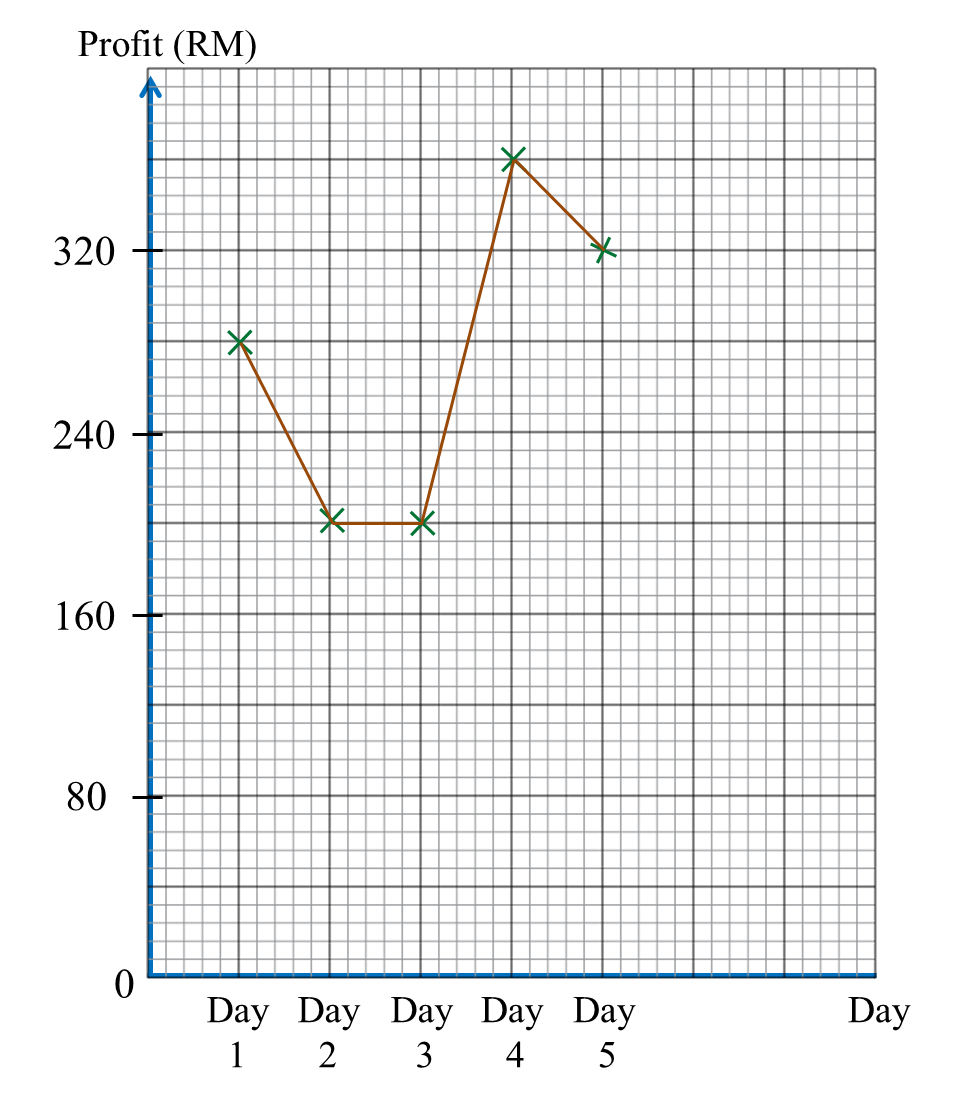
Table below shows the profit made from the sales of coconut at a stall over five days.
|
Day
|
Day 1
|
Day 2
|
Day 3
|
Day 4
|
Day 5
|
|
Profit (RM)
|
280
|
200
|
200
|
360
|
320
|
On diagram in the answer space, draw a line graph to represent all the information in the Table. Use the scale 2 cm to RM80 on the vertical axis.
Answer:
Solution:

Question 5:
Table below shows the number of students who read four types of books.
|
Types of books
|
Fiction
|
Language
|
Technology
|
Religion
|
|
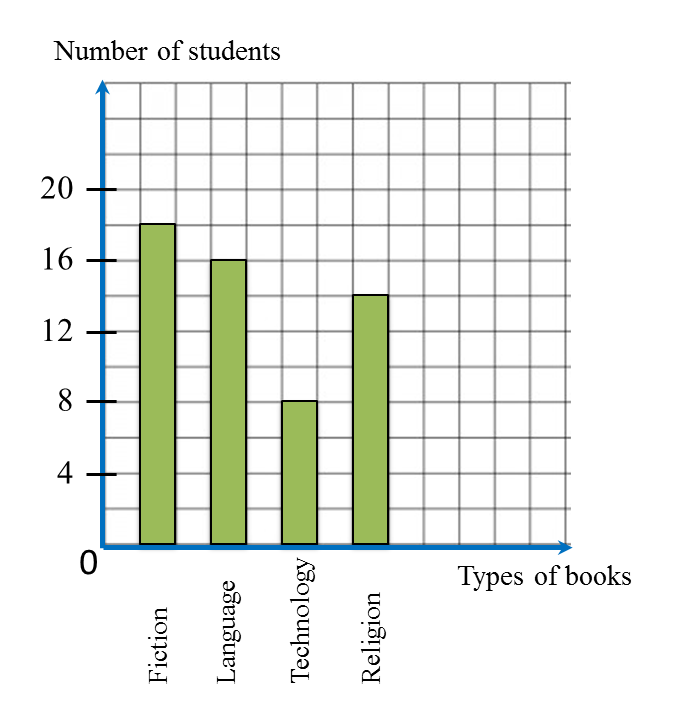
Number of students
|
18
|
16
|
8
|
14
|
On diagram in the answer space, draw a bar chart to represent all the information in the Table.
Answer:
Solution:

Question 6:
Diagram below is an incomplete bar chart which shows the number of cars sold in a shop for duration of five months.
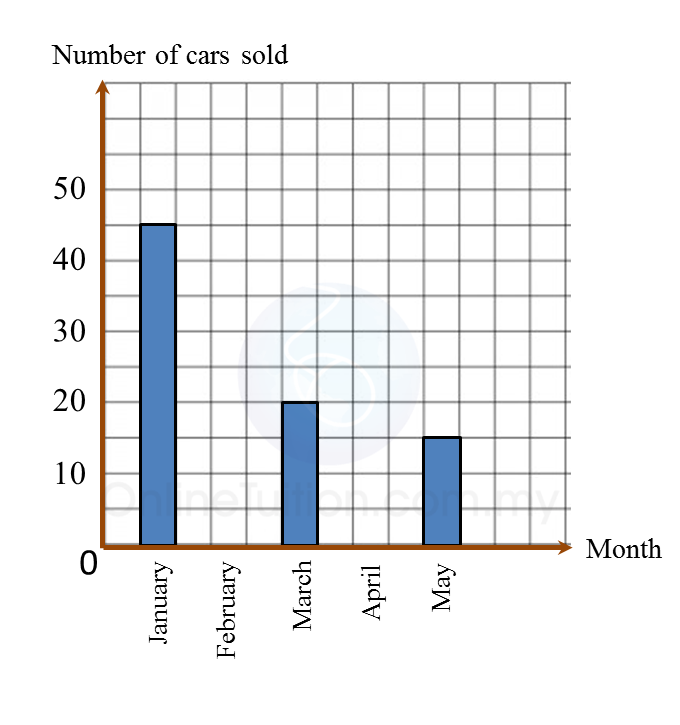 (a) The number of cars sold for the five months is 150 units. The number of cars sold in February is equal to the number of cars sold in April.
(a) The number of cars sold for the five months is 150 units. The number of cars sold in February is equal to the number of cars sold in April.
Complete the bar chart in the Diagram.
(b) Find the percentage of cars sold in January.
Solution:
(a)
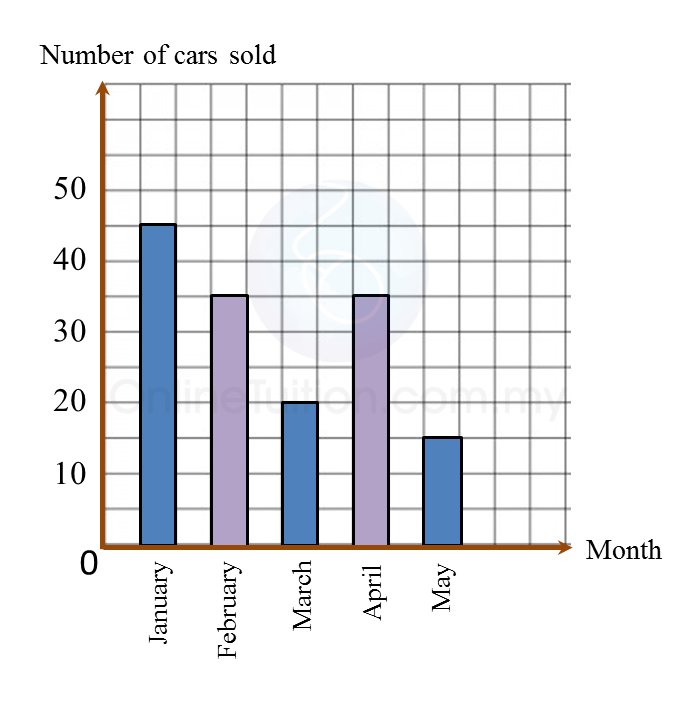 (b)
(b)
Diagram below is an incomplete bar chart which shows the number of cars sold in a shop for duration of five months.
 (a) The number of cars sold for the five months is 150 units. The number of cars sold in February is equal to the number of cars sold in April.
(a) The number of cars sold for the five months is 150 units. The number of cars sold in February is equal to the number of cars sold in April.Complete the bar chart in the Diagram.
(b) Find the percentage of cars sold in January.
Solution:
(a)
 (b)
(b)13.2.1 Statistics (I), PT3 Focus Practice
13.2.1 Statistics (I), PT3 Focus Practice
Question 1:
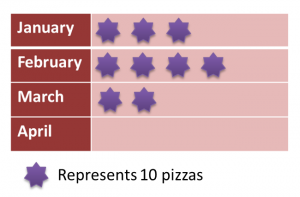
Diagram below is a pictograph showing the number of pizzas sold in three months.
The price of one pizza is RM18. The total sales for those four months are RM2250.
Calculate the number of pizzas sold in April.
Solution:
Total number of pizzas sold in four months
Total number of pizzas sold in first three months
= 9 × 10
= 90
Number of pizzas sold in April
= 125 – 90
= 35
Question 2:
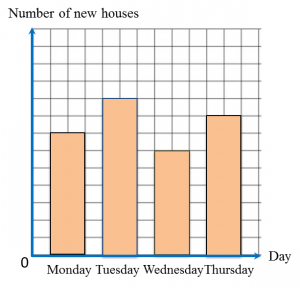
Diagram below is a bar chart showing the number of new houses sold over four days.
The total number of new houses sold on Wednesday and Thursday is 56.
Calculate the total number of new houses sold on Monday and Tuesday.
Solution:
Wednesday: 12 units
Thursday: 16 units
Number of houses represented by 1 unit
Monday: 14 units
Tuesday: 18 units
Total number of new houses sold on Monday and Tuesday
= (14 + 8) × 2
= 64Question 3:
Table below shows the number of companies that gave contributions to an orphan fund over a period of five days.
|
Days
|
Monday
|
Tuesday
|
Wednesday
|
Thursday
|
Friday
|
|
Number of companies
|
8
|
14
|
m
|
17
|
11
|
It is given that 20% of the total contribution was made on Tuesday.
Calculate the value of m.
Solution:
Let C = Total contribution
12.2.1 Solid Geometry (II), PT3 Focus Practice
12.2.1 Solid Geometry (II), PT3 Focus Practice
Question 1:
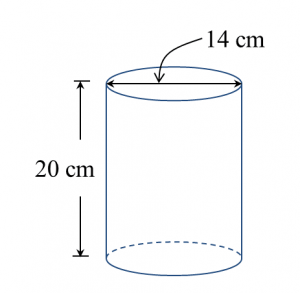
Diagram below shows closed right cylinder.
Calculate the total surface area, in cm2, of the cylinder.
Solution:
Total surface area
= 2(πr2) + 2πrh
Question 2:
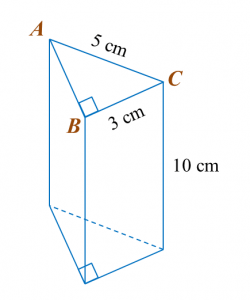
Diagram below shows a right prism with right-angled triangle ABC as its uniform cross section.
Calculate the total surface area, in cm2, of the prism.
Solution:
Total surface area
= 2 (½× 3 × 4) + (3 × 10) + (4 × 10) + (5 × 10)
= 12 + 30 + 40 + 50
= 132 cm2Question 3:
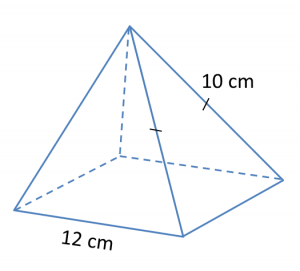
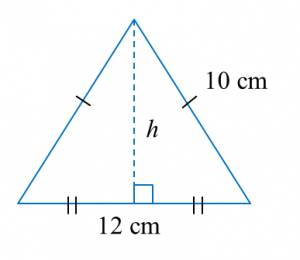
Diagram below shows a right pyramid with a square base.
Calculate the total surface area, in cm2, of the right pyramid.
Solution:
h2= 102 – 62
= 100 – 36
= 64
h = √64
= 8cm
Total surface area of the right pyramid
= (12 × 12) + 4 × (½× 12 × 8)
= 144 + 192
= 336 cm2