Question 6:
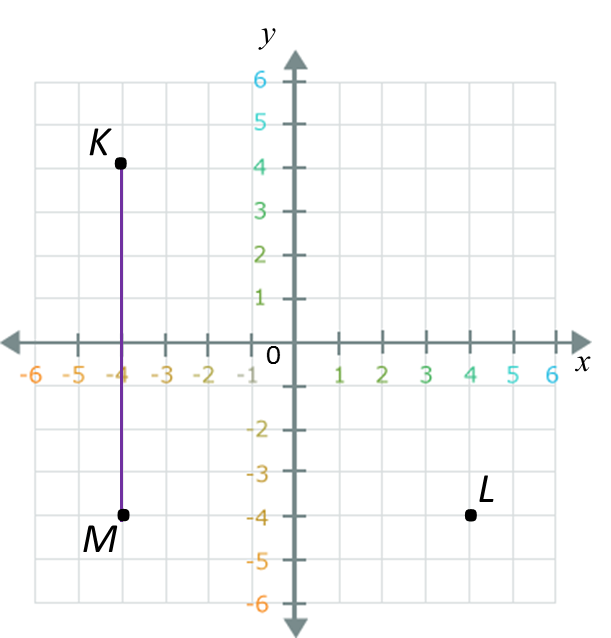
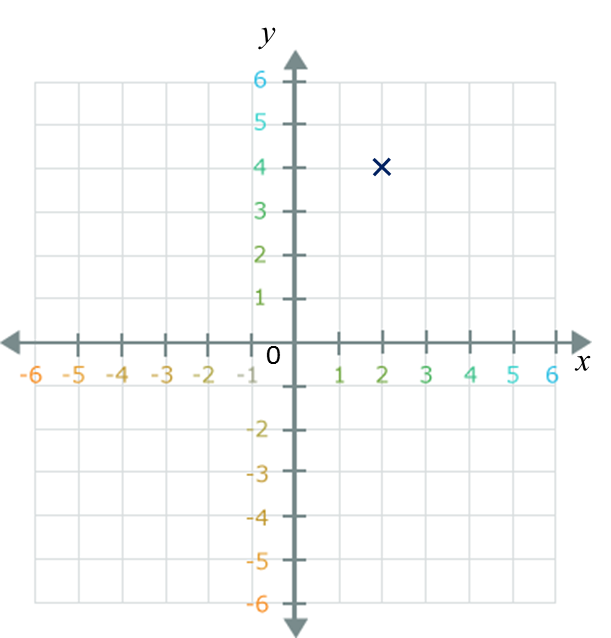
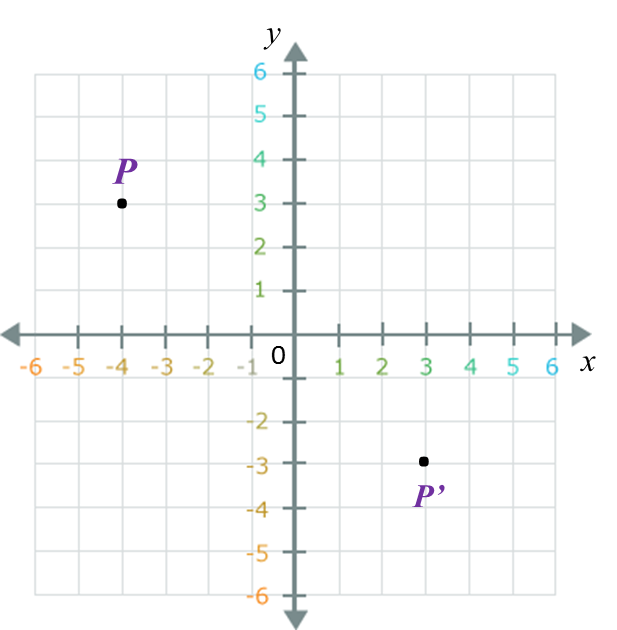
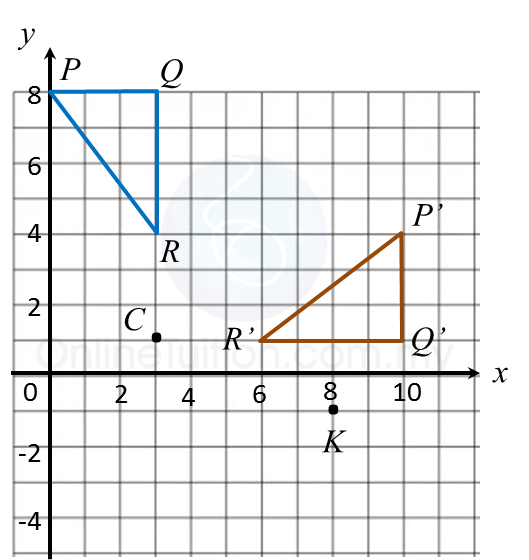
Diagram in the answer space shows a Cartesian plane board used in an indoor game.
The instruction of the game is such that the first move follows the translation and the second move follows the translation .
Jimmy starts moving from the position mark x.
(a) Mark T1 at Jimmy’s position after the first move and T2 at the position after the second move.
(b) State the coordinates of the position based on Jimmy’s final move.
Answer:
Solution:
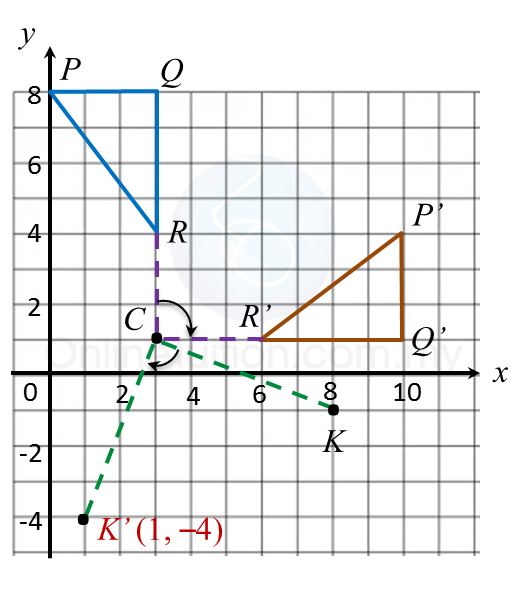
(a)
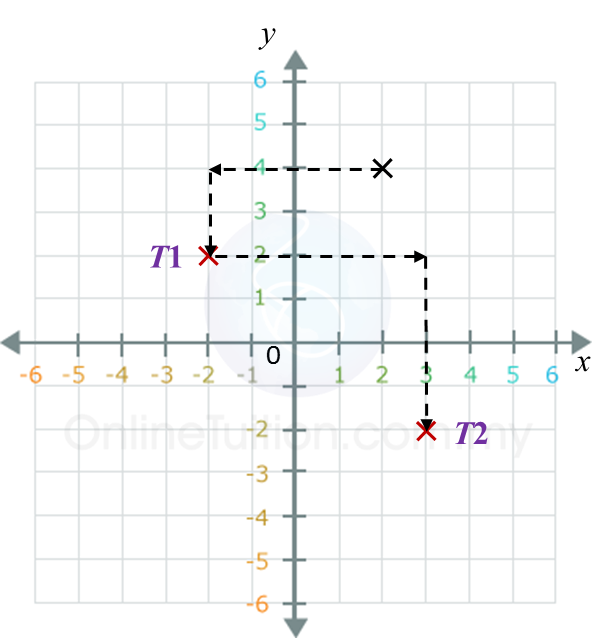
(b) Jimmy’s final position = (3, –2).
Diagram in the answer space shows a Cartesian plane board used in an indoor game.
The instruction of the game is such that the first move follows the translation and the second move follows the translation .
Jimmy starts moving from the position mark x.
(a) Mark T1 at Jimmy’s position after the first move and T2 at the position after the second move.
(b) State the coordinates of the position based on Jimmy’s final move.
Answer:

Solution:
(a)

(b) Jimmy’s final position = (3, –2).
Question 7:
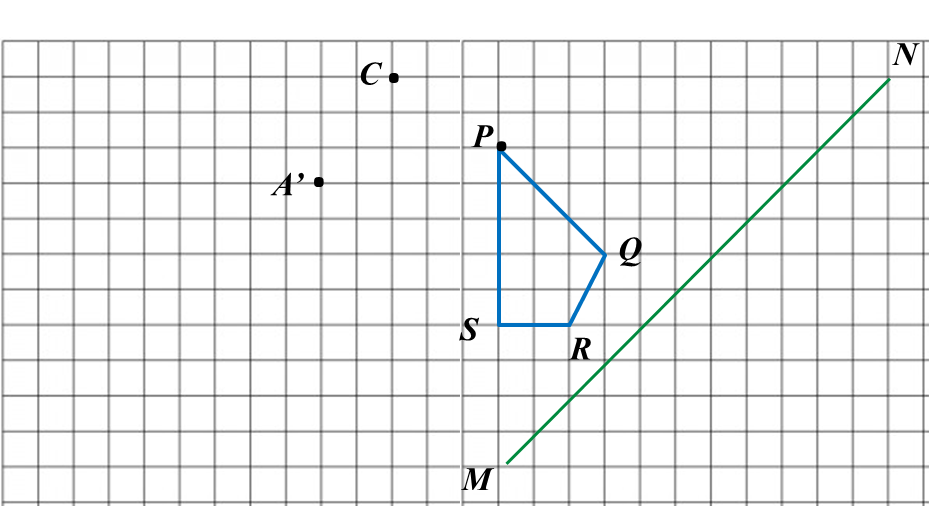
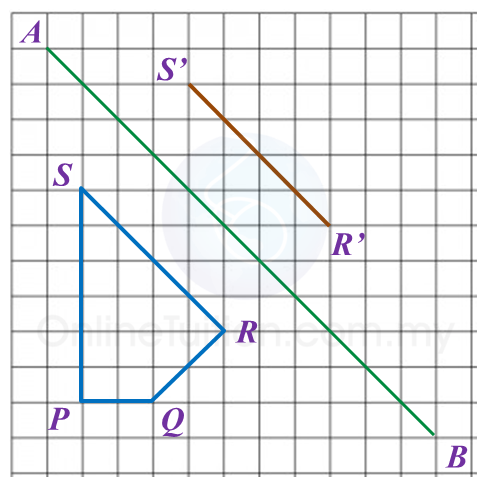
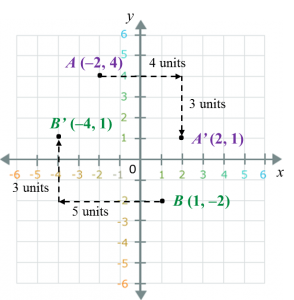
In the answer space below, a quadrilateral PQRS is drawn on a grid of squares. A’ is the image of P under rotation 90o at point C.
(a) State the direction of the rotation.
In the answer space,
(b) mark B’ as the image of point Q under the same rotation.
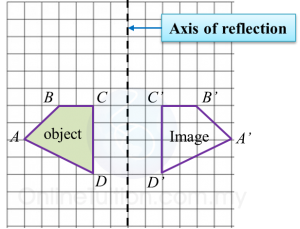
(c) draw the image of quadrilateral PQRS under a reflection on the line MN.
Answer:
Solution:
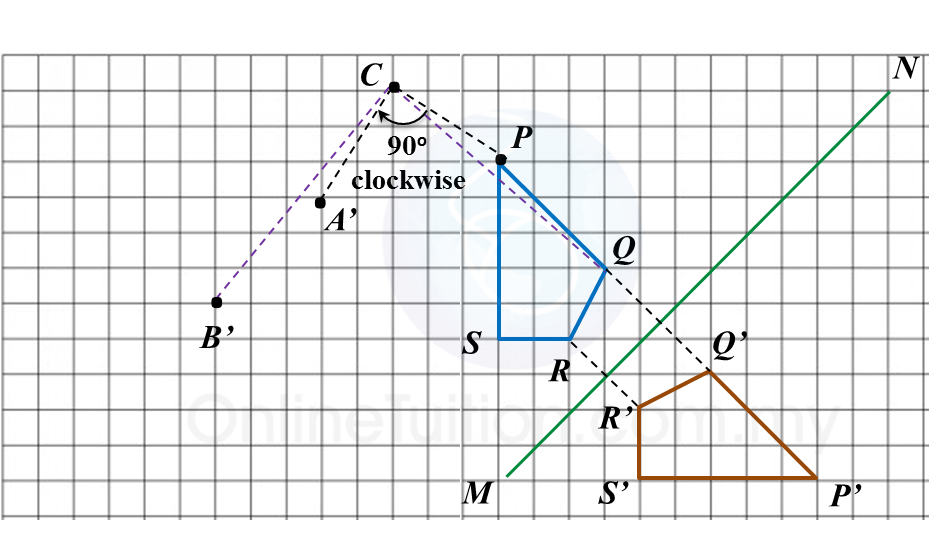
(a) A’ is the image of P under a rotation of 90o clockwise about the centre C.
(b) and (c)
In the answer space below, a quadrilateral PQRS is drawn on a grid of squares. A’ is the image of P under rotation 90o at point C.
(a) State the direction of the rotation.
In the answer space,
(b) mark B’ as the image of point Q under the same rotation.
(c) draw the image of quadrilateral PQRS under a reflection on the line MN.
Answer:

Solution:
(a) A’ is the image of P under a rotation of 90o clockwise about the centre C.
(b) and (c)

Question 8:
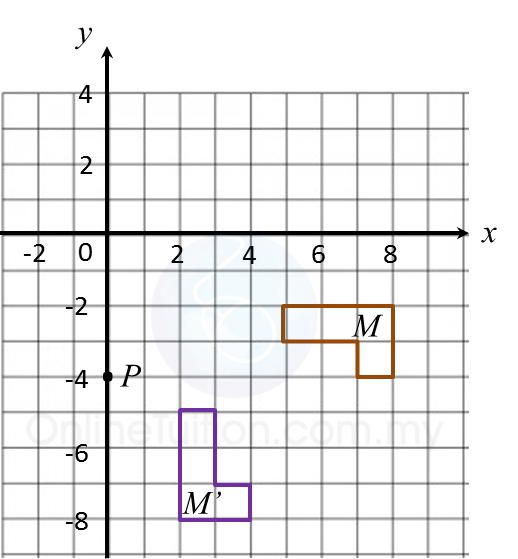
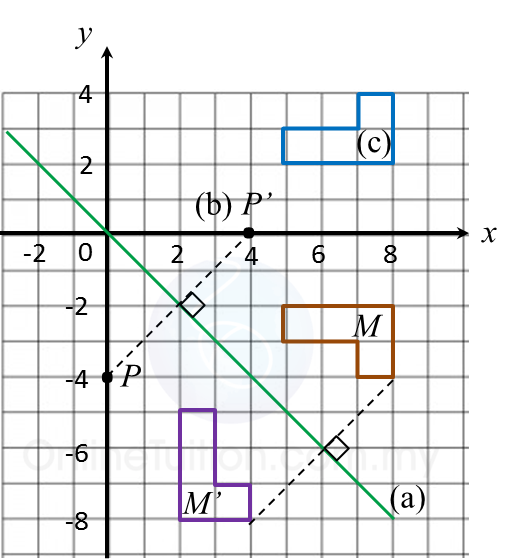
Diagram in the answer space shows trapezium ABCD drawn on a Cartesian plane. A’D’ is the image of AD under a rotation at centre W.
(a) State
(i) angle of rotation
(ii) the direction of the rotation.
(b) On diagram in the answer space, complete the image of trapezium ABCD.
Answer:
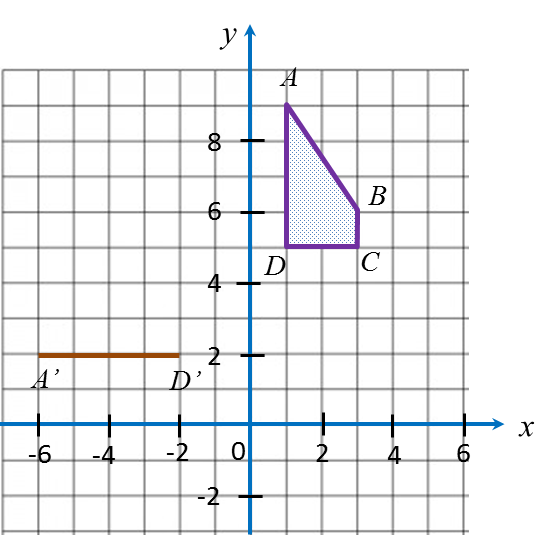
Solution:
(a)(i)
(a)(ii) Anticlockwise or clockwise.
(b)
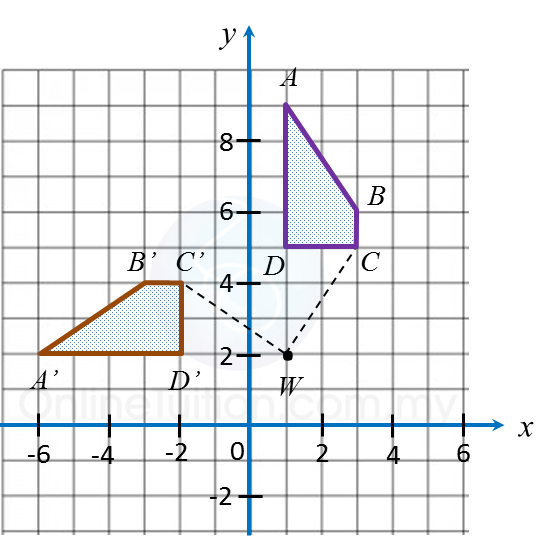
Diagram in the answer space shows trapezium ABCD drawn on a Cartesian plane. A’D’ is the image of AD under a rotation at centre W.
(a) State
(i) angle of rotation
(ii) the direction of the rotation.
(b) On diagram in the answer space, complete the image of trapezium ABCD.
Answer:

Solution:
(a)(i)
(a)(ii) Anticlockwise or clockwise.
(b)

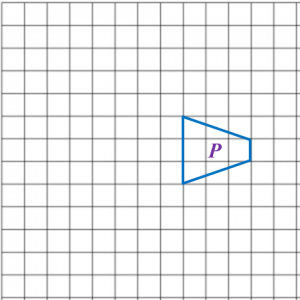
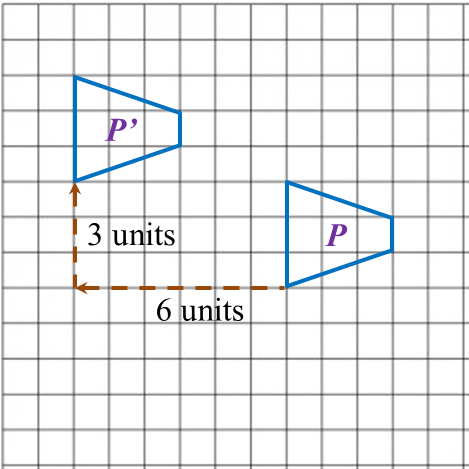


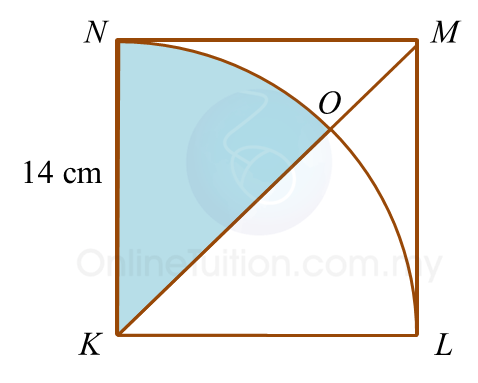
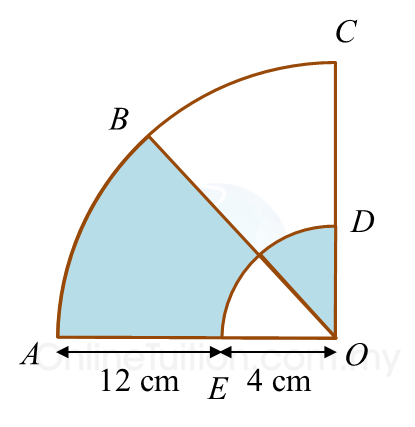
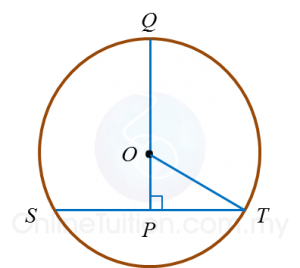
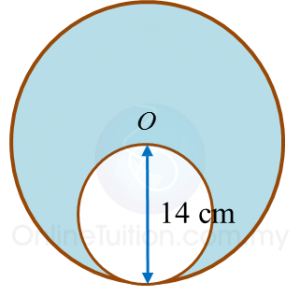
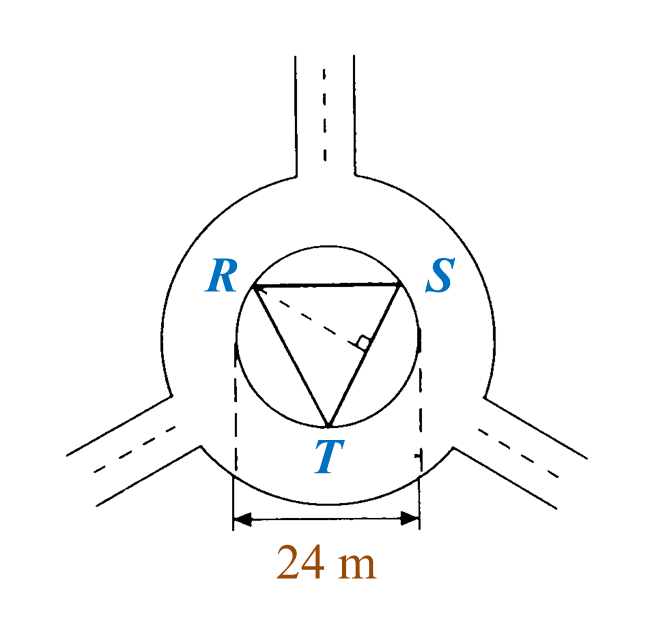 Find the perimeter of the platform.
Find the perimeter of the platform.