Home › Archive for PT3 Maths › Page 8

PT3 Maths

8.2.3 Coordinates, PT3 Focus Practice

Posted on by

Question 11:
Diagram below shows the route of a Negaraku Run.
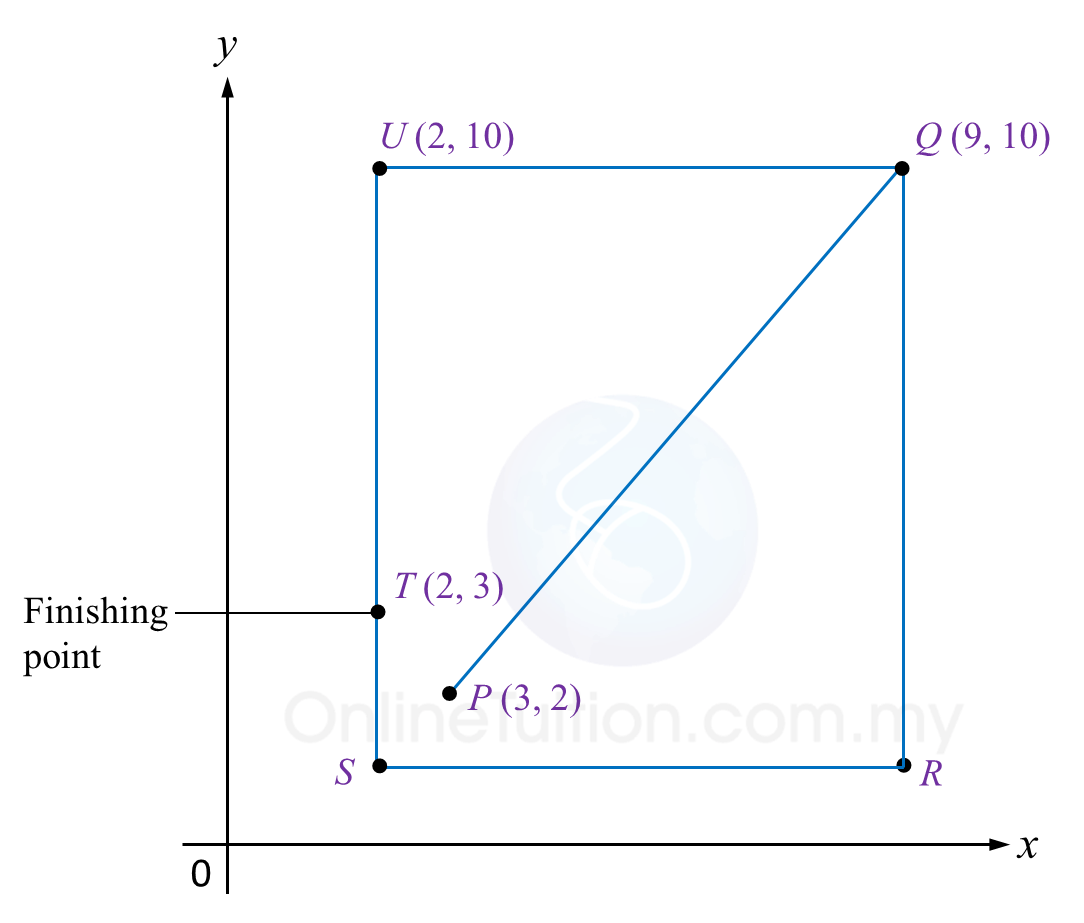The route of male participants is PQUT while the route for female participants is QRST. QR is parallel to UT whereas UQ is parallel to SR.
(a) Given the distance between point Q and point R is 9 km, state the coordinates of point R.
(b) It is given that the male participants start the run at point P and the female participants at point Q.
Find the difference of distance, in km, between the male and female participants.

Solution:
(a)
R = (9, 1)

(b)
Route of male participants
= PQ + QU + UT
= 10 + 7 + 7
= 24 km

Route of female participants
= QR + RS + ST
= 9 + 7 + 2
= 18 km

Difference in distance
= 24 – 18
= 6 km


Question 12:
Diagram below shows a parking lot in the shape of trapezium, RSTU. Two coordinates from the trapezium vertices are R(–30, –4) and S(20, –4).

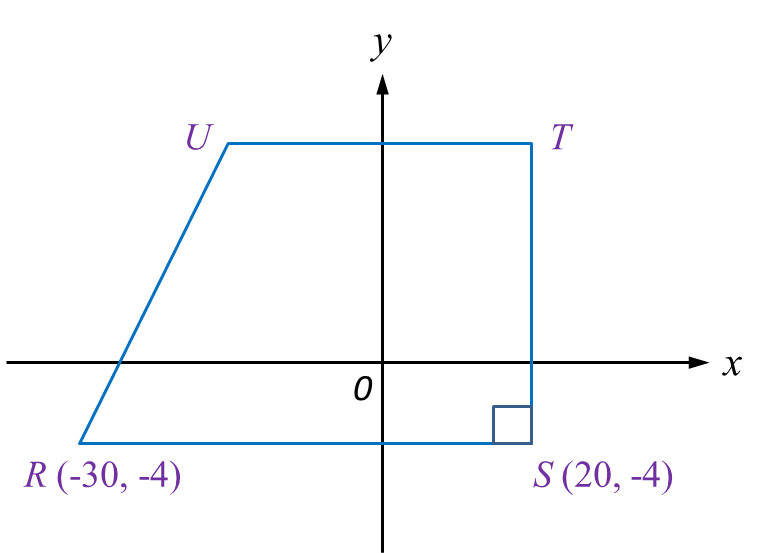
(a) Given the distance between vertex S and vertex T is 22 units.
State the coordinates of vertex T.
(b) Given the area of the parking lot is 946 unit2, find the coordinates of U.

Solution:
(a)
y-coordinates of T = –4 + 22 = 18  
T = (20, 18)

(b)
 Area of trapezium=946  unit 2 1 2 ×( UT+RS )×ST=946 1 2 ×( UT+50 )×22=946 UT+50= 946×2 22 UT+50=86 UT=36 x−coordinate of point U=20−36=−16 y−coordinate of point U=18 U=( −16,18 )

8.2.1 Coordinates, PT3 Focus Practice

Posted on by

8.2.1 Coordinates, PT3 Focus Practice

Question 1:
In diagram below, Q is the midpoint of the straight line PR.
The value of m is

Solution:
2 + m 2 = 5 2 + m = 10 m = 8


Question 2:
In diagram below, P and Q are points on a Cartesian plane.
 
 
If M is the midpoint of PQ, then the coordinates of M are

Solution:
P( −4,8 ), Q( 6,−2 ) Coordinates of M =( −4+6 2 , 8+( −2 ) 2 ) =( 1,3 )


Question 3:
Find the distance between P (–4, 6) and Q (20, –1).

Solution:
Distance of PQ = ( −4−20 ) 2 + [ 6−( −1 ) ] 2 = ( −24 ) 2 + 7 2 = 576+49 = 625 =25 units


Question 4:
Diagram shows a straight line PQ on a Cartesian plane.
 
Calculate the length, in unit, of PQ.

Solution:
PS = 15 – 3 = 12 units 
SQ = 8 – 3 = 5 units 
By Pythagoras’ theorem,
PQ2 = PS2 + SQ2
= 122+ 52
PQ = √169
  = 13 units


Question 5:
The diagram shows an isosceles triangle STU.
 
Given that ST = 5 units, the coordinates of point S are

Solution:
 
For an isosceles triangle STU, M is the midpoint of straight line TU.
x−coordinate of M = −2+4 2 =1
Point M = (1, 0)
 
MT = 4 – 1 = 3 units 
By Pythagoras’ theorem,
SM2 = ST2 – MT2
= 52 – 32
= 25 – 9
= 16
SM = √16
= 4
Therefore, point S = (1, 4).

8.1 Coordinates

Posted on by

8.1 Coordinates

8.1.1 Coordinates
1. The Cartesian coordinate system is a number plane with a horizontal line (x-axis) drawn at right angles to a vertical line (y-axis), intersecting at a point called origin.

2. It is used to locate the position of a point in reference to the x-axis and y-axis.

3. The coordinate of any point are written as an ordered pair (x, y).  The first number is the x-coordinate and the second number is the y-coordinate of the point.
 
Example:
 
The coordinates of points A and B are (3, 4) and (–5, –2) respectively.
This means that point A is located 3 units from they-axis and 4 units from the x-axis, whereas point B is located 5 units on the left from the y-axis and 2 units from the x-axis. 

4. The coordinate of the origin O is (0, 0). 


8.1.2 Scales for the Coordinate Axes
1. The scale for an axis is the number of units represented by a specific length along the axes.

2. The scale on a coordinate is usually written in the form of a ratio.
Example:
A scale of 1 : 2 means one unit on the graph represents 2 units of the actual length.

3. Both coordinate axes on the Cartesian plane may have
(a) the same scales, or
(b) different scales.
Example:
 
1 unit on the x-axis represents 2 units.
1 unit on the y-axis represents 1 unit.
Therefore the scale for x-axis is 1 : 2 and the scale for y-axis is 1 : 1.
Coordinates of:
P (4, 3) and Q (10, 5).


8.1.3 Distance between Two Points
1. Finding the distance between two points on a Cartesian plane is the same as finding the length of the straight line joining them.
 
2. The distance between two points can be calculated by using Pythagoras’ theorem.
Example:
AB = 2 – (–4) = 2 + 4 = 6 units  
BC = 5 – (–3) = 5 + 3 = 8 units  
By Pythagoras’ theorem,
AC2 = AB2 + AC2
= 62 + 82
AC = √100
  = 10 units
3. Distance is always a positive value.


8.1.4 Midpoint
The midpoint of a straight line joining two points is the middle point that divides the straight line into two equal halves.
Midpoint, M = ( x 1 + x 2 2 , y 1 + y 2 2 )

Example:
The coordinate of the midpoint of (7, –5) and (–3, 11) are
( 7 + ( − 3 ) 2 , − 5 + 11 2 ) = ( 4 2 , 6 2 ) = ( 2 , 3 )
 

7.2.3 Geometrical Constructions, PT3 Focus Practice

Posted on by

Question 6:
Diagram below in the answer space shows part of a triangle ABC.
(a) Using a pair of compasses, protractor and ruler, draw the    triangle ABC with AB=7 cm, ∠ABC= 65 o  and BC=5 cm. (b) Measure ∠ACB.

Answer:
(a)



Solution:
(a)


(b)
∠ACB= 72 o



Question 7:
Diagram below shows a quadrilateral ABQR.


(a) Using only a ruler and a pair of compasses, construct the diagram using the measurement given.
Begin from the straight lines AB and BQ provided in the answer space.
(b) Based on the diagram constructed in (a), measure the length, in cm, of QR.

Answer:
(a)



Solution:
(a)


(b)
QR = 5.9 cm

7.2.2 Geometrical Constructions, PT3 Focus Practice

Posted on by

7.2.2 Geometrical Constructions, PT3 Focus Practice 2

Question 4:
Diagram below shows a parallelogram PQRS. The point T lies on PQ such that ST is perpendicular to PQ.


 
Using only a ruler and a pair of compasses, construct parallelogram PQRS, beginning from the lines PQ and PS provided in the answer space.

Answer:
 


Solution:


Question 5:
Diagram below shows a triangle ABC.


 
(a) Using only a ruler and a pair of compasses, construct triangle ABC, beginning with the straight line BC in the answer space.
(b)   Hence, measure the length, in cm, of BA.

Answer:
(a)



Solution:
(a)

 
 
(b)
BA = 4.5 cm

7.2.1 Geometrical Constructions, PT3 Focus Practice

Posted on by

7.2.1 Geometrical Constructions, PT3 Focus Practice
Question 1:
Diagram below in the answer space shows part of triangle ABC.
(a) Using a pair of compasses, a protractor and a ruler, draw a triangle ABC starting from the line given in the answer space with AB = 4.5 cm, BC = 6 cm and ∠ABC = 105o.
(b) Measure ∠BCA.

Answer:
(a)

 

Solution:
(a)


(b)
∠BCA = 31o


Question 2:
Diagram below shows a triangle ABC drawn not to scale.

 
Diagram in the answer space shows a straight line AB.
(a) Using only a ruler and a pair of compasses, construct
 (i) triangle ABC to the measurements shown in diagram above,
 (ii)   the perpendicular line to the straight line AC which passes through the point B.
(b)   Measure the perpendicular distance between straight line AC and point B.

Answer:
(a)(i),(ii)

 

Solution:
(a)(i),(ii)

 (b)
5.3 cm


Question 3:
Diagram below shows a pentagon ABCDE.


Using only a ruler and a pair of compasses, construct the diagram, beginning from the straight lines CD and DE provided in the answer space.
 
Answer:

Solution:

 

6.2.2 Pythagoras’ Theorem, PT3 Focus Practice

Posted on by

Question 6:
In diagram below, ABCH is a square and DEFG is a rectangle. HCDE is a straight line and HC = CD.

Find the perimeter, in cm, of the whole diagram.

Solution:
G H 2 =D H 2 +D G 2    = 24 2 + 7 2    =576+49    =625 GH=25 cm Perimeter of the whole diagram =12+12+12+26+7+14+25 =108 cm

Question 7:
In the diagram, ABC and EFD are right-angled triangles.


Calculate the perimeter, in cm, of the shaded region.

Solution:
D E 2 = 3 2 + 4 2    =9+16    =25 DE= 25  =5 cm A C 2 = 7 2 + 24 2    =49+576    =625 AC= 625  =25 cm Perimeter of the shaded region =24+7+( 25−5 )+3+4 =58 cm

Question 8:
In the diagram, ABD and BCE are right-angled triangles. ABC and DBE are straight lines. The length of AB is twice the length of BC.


Calculate the length, in cm, of CE.

Solution:
A B 2 = 25 2 − 7 2    =625−49    =576 AB= 576  =24 cm BC=24 cm÷2  =12 cm C E 2 = 5 2 + 12 2    =25+144    =169 CE= 169  =13 cm

Question 9:
Diagram below shows two right-angled triangles, ABE and CBD. BED is a straight line.
Find the length, in cm, of BC. Round off the answer to two decimal places.

Solution:
3 2 +B E 2 = 5 2    B E 2 = 5 2 − 3 2 =16 BE=4 cm B C 2 + ( 5+4 ) 2 = 17 2    B C 2 = 17 2 − 9 2 =208  BC= 208  BC=14.42 cm


Question 10:
Diagram below shows two right-angled triangles, ABC and ADE. ACD is a straight line.
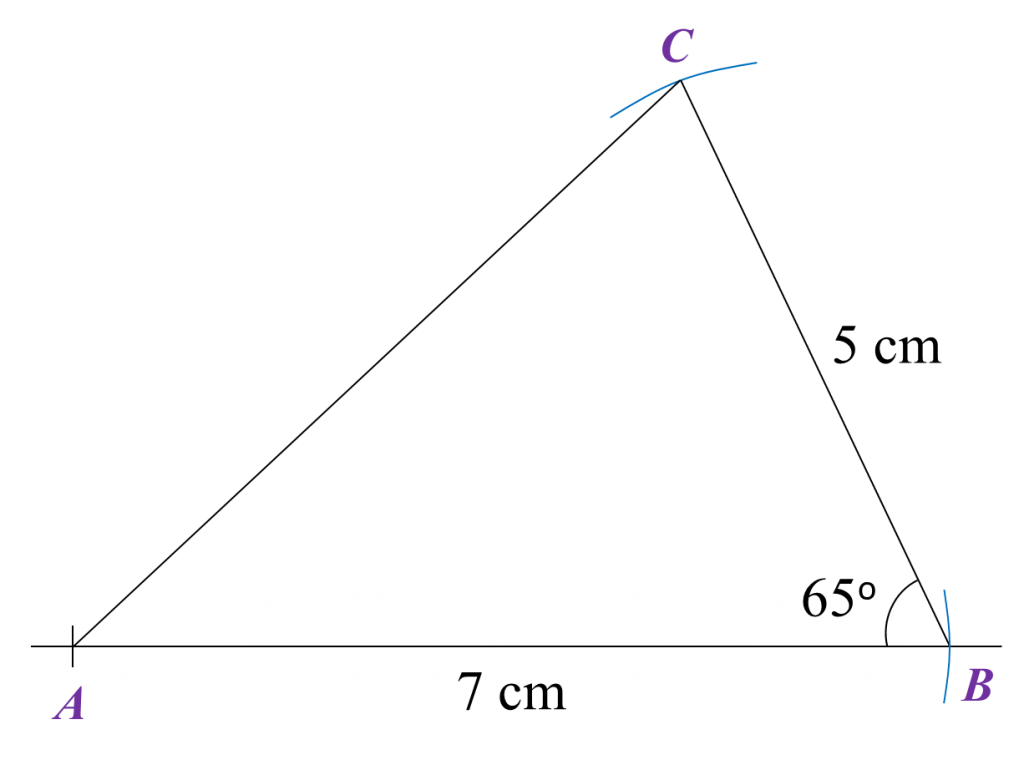
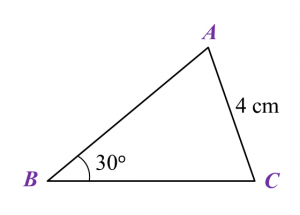
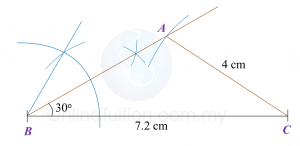
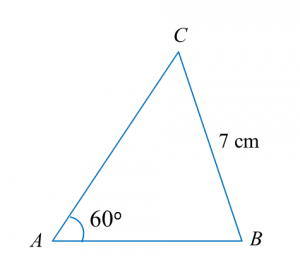
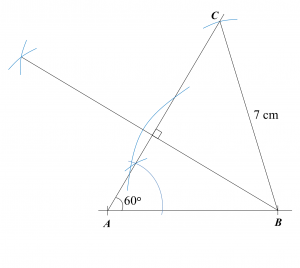
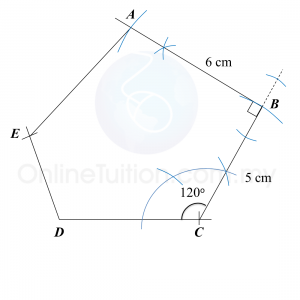
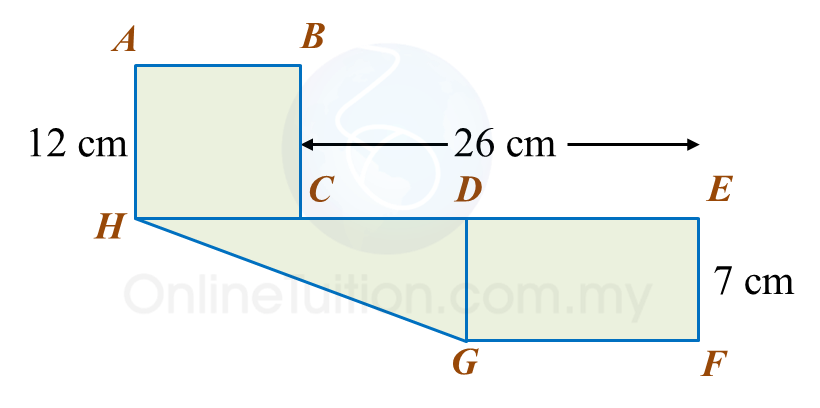
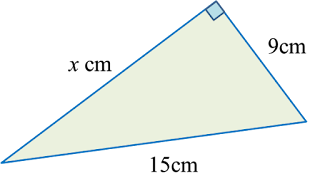
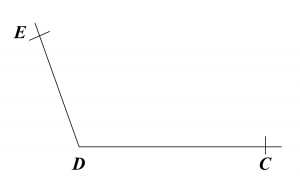
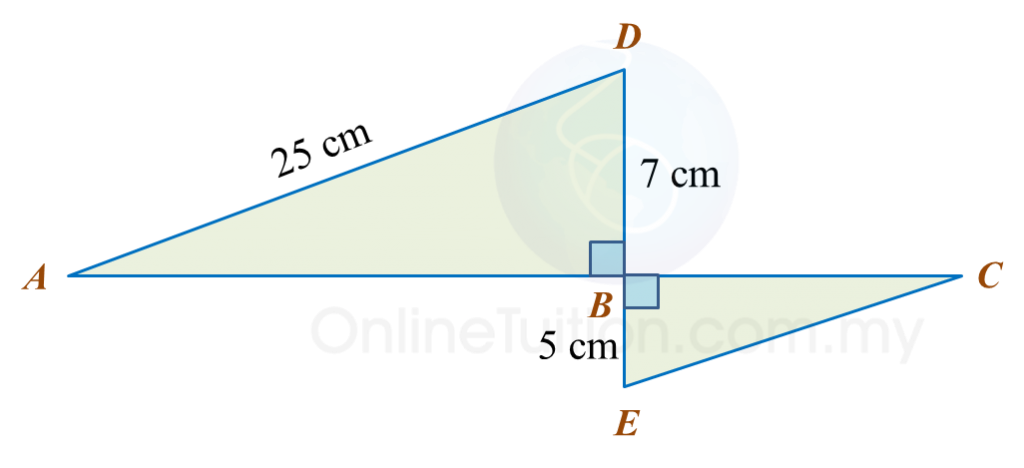
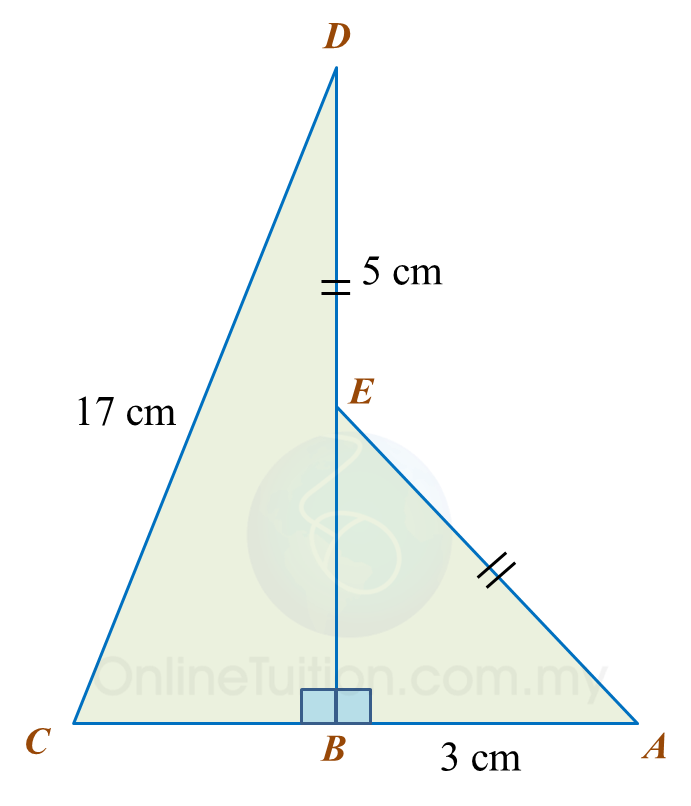
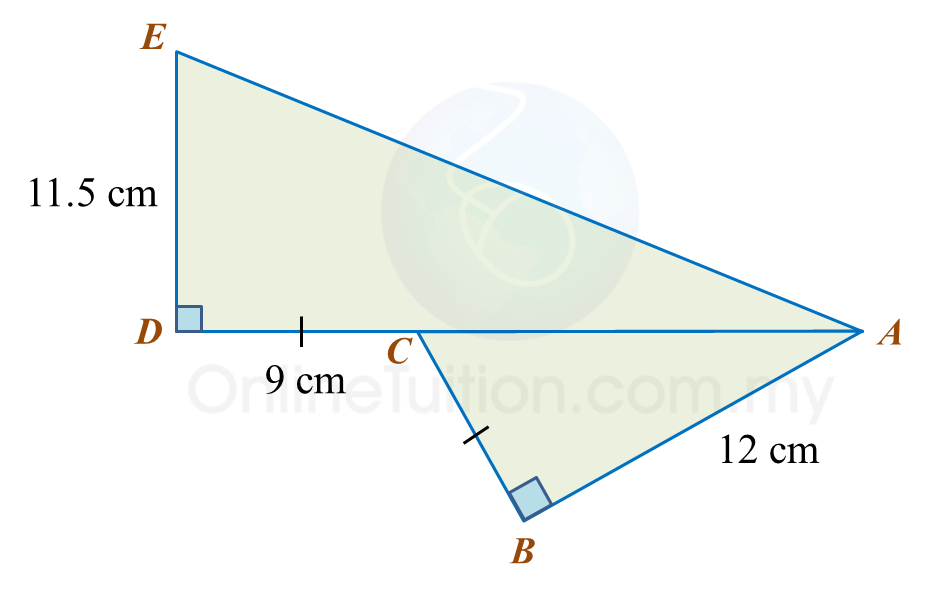Find the length, in cm, of AE. Round off the answer to one decimal places.

Solution:
A C 2 = 12 2 + 9 2    =225 AC= 225  =15 cm A E 2 = ( 15+9 ) 2 + 11.5 2    =576+132.25    =708.25 AE= 708.25  =26.6 cm

6.2.1 Pythagoras’ Theorem, PT3 Focus Practice

Posted on by

6.2.1 Pythagoras’ Theorem, PT3 Focus Practice
 
Question 1:
In the diagram, ABC is a right-angled triangle and BCD is a straight line. Calculate the length of AD, correct to two decimal places.

Solution:
In ∆ ABC,
BC2 = 52 – 42
= 25 – 16
= 9
BC = √9
  = 3 cm

In ∆ ABD,
BD = BC + CD
  = 3 + 6
  = 9
AD2 = 42 + 92
= 16 + 81
= 97
AD = √97
  = 9.849
  = 9.85 cm


Question 2:
In the diagram shows two right-angled triangles. Calculate the perimeter of the whole diagram.

Solution:
In ∆ ABC,
AC2 = 62 + 82
= 36 + 64
= 100
AC = √100
  = 10 cm
AD = 5 cm

In ∆ EDC,
EC2 = 122 + 52
= 144 + 25
= 169
EC = √169
  = 13 cm

Perimeter of the whole diagram
= AB + BC + CE + DE + AD
= 6 + 8 + 13 + 12 + 5
= 44 cm


Question 3:
Diagram below shows a triangle ACD and ABC is a straight line.
Calculate the length, in cm, of AD.

Solution:
In ∆ DBC,
BC2 = 252 – 242
= 625 – 576
= 49
BC = √49
  = 7 cm
AB = 17 – 7 = 10 cm

In ∆ DAB,
AD2 = 102 + 242
= 100 + 576
= 676
AD = √676
  = 26 cm


Question 4:
In diagram below ABDE is a square and EDC is a straight line.
The area of the square ABDE is 144 cm2.
Calculate the length, in cm, of BC.

Solution:
BD = √144
  = 12 cm
BC2 = 122 + 92
= 144 + 81
= 225
BC = √225
  = 15 cm


Question 5:
In the diagram, ABCD is a trapezium and AED is a right-angled triangle.
 
Calculate the area, in cm2, of the shaded region.

Solution:
AD2 = 52 + 122
= 25 + 144
= 169
AD = √169
  = 13 cm
Area of trapezium ABDC
= ½ (13 + 15) × 9
= 126 cm2

Area of triangle AED
= ½ × 5 × 12
= 30 cm2

Area of the shaded region
= 126 – 30
= 96 cm2

6.1 Pythagoras’ Theorem

Posted on by

6.1 Pythagoras’ Theorem

6.1.1 Pythagoras’ Theorem
1. In a right-angled triangle, the hypotenuse is the longest side of the triangle.
2. Pythagoras’ Theorem:

  In a right-angled triangle, the square
  of the hypotenuse is equal to the sum
  of the squares of the other two sides.
Example 1:
 
Solution:
x 2 = 5 2 + 12 2 = 25 + 144 x = 169 = 13  

Example 2:
 
Solution:
x 2 = 15 2 − 9 2 = 225 − 81 x = 144 = 12

3. Pythagorean triples are three whole numbers that form the sides of a right-angled triangle.

Example:
(a) 3, 4, 5
(b) 6, 8, 10
(c) 5, 12, 13
(d) 8, 15, 17
(e) 9, 12, 15


6.1.2 The Converse of the Pythagoras’ Theorem
 
 
  In a triangle, if the sum of the squares of the two sides
  is equal to the square of the longest side, then the angle
  opposite the longest side is a right angle.

5.2.3 Ratio, Rates and Proportions (I), PT3 Focus Practice

Posted on by

Question 11:
Diagram below shows two baskets of eggs.

(a) State the ratio of the number of chicken eggs to the number of duck eggs.
(b) A number of eggs need to be added into each basket so that the ratio in (a) remain unchanged. Find the minimum number of eggs to be added in each basket.

Solution: 
(a)
Ratio of the number of chicken eggs to the number of duck eggs
= 12 : 16
= 3 : 4

(b)
Let the number of eggs need to be added into each basket = n
Total number of eggs need to be added into each basket
= 3n + 4n

Minimum value of n = 1
Hence, the minimum number of eggs to be added into each basket
= 3(1) + 4(1)
= 3 + 4
= 7 (3 chicken eggs and 4 duck eggs need to be added to each basket)  

 


Question 12:
Diagram below shows two baskets, A and B, filled with candies.
(a) State the ratio of the number of candies in basket A to the number of candies in basket B.
(b) If 20 candies are added into basket A, calculate the number of candies which need to be added into basket B so that the ratio in (a) remain unchanged.

Solution: 
(a)
Ratio of the number of candies in basket A to the number of candies in basket B
= 10 : 12
= 5 : 6

(b)
If 20 candies are added into basket A, the number of candies which need to be added into basket B so that the ratio 5 : 6 remain unchanged
= 20 ÷ 5 × 6
= 4 × 6
= 24

 


Question 13:
Karim built two towers using toy bricks of the same size as shown in Diagram below.

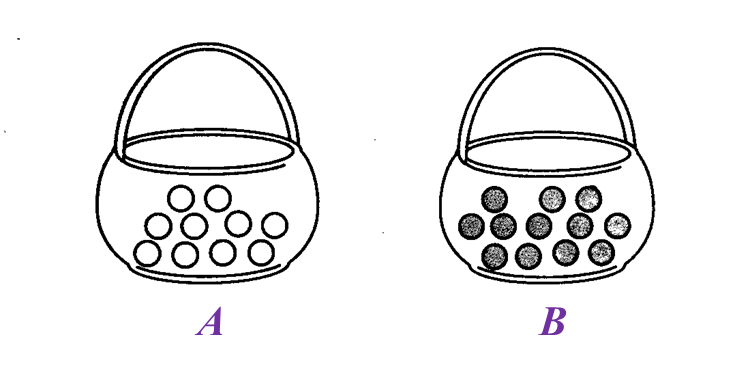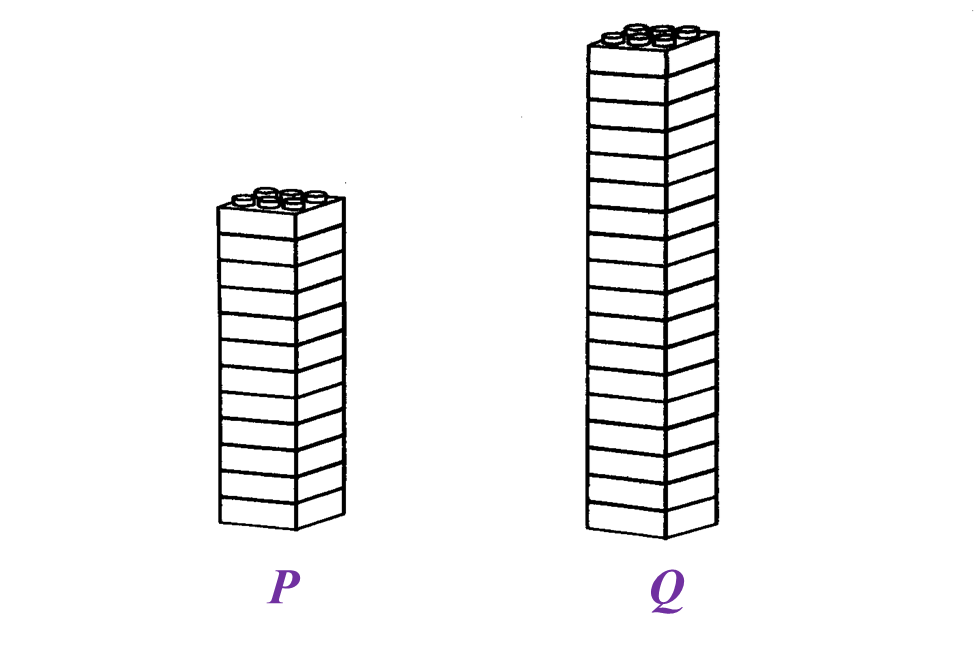(a) State the ratio of the number of toy bricks in Tower P to the number of toy bricks in Tower Q.
(b) A number of toy bricks need to be removed from each tower so that the ratio in (a) remains unchanged.
Find the total number of toy bricks to be removed from each tower.

Solution: 
(a)
Tower P : Tower Q
= 12 : 18
= 2 : 3

(b)
Let number of toy bricks to be removed from each tower = n
Total number of bricks to be removed
= 2n + 3n
2(1) + 3(1) = 2 + 3 = 5 → (2 bricks from tower P, 3 bricks from tower Q)
2(2) + 3(2) = 4 + 6 = 10 → (4 bricks from tower P, 6 bricks from tower Q)
2(3) + 3(3) = 6 + 9 = 15 → (6 bricks from tower P, 9 bricks from tower Q)
2(4) + 3(4) = 8 + 12 = 20 → (8 bricks from tower P, 12 bricks from tower Q)
2(5) + 3(5) = 10 + 15 = 25 → (10 bricks from tower P, 15 bricks from tower Q)