Question 9:
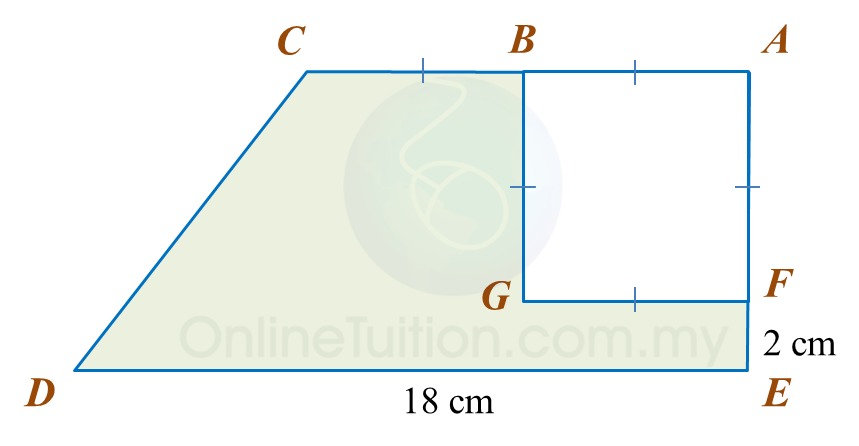
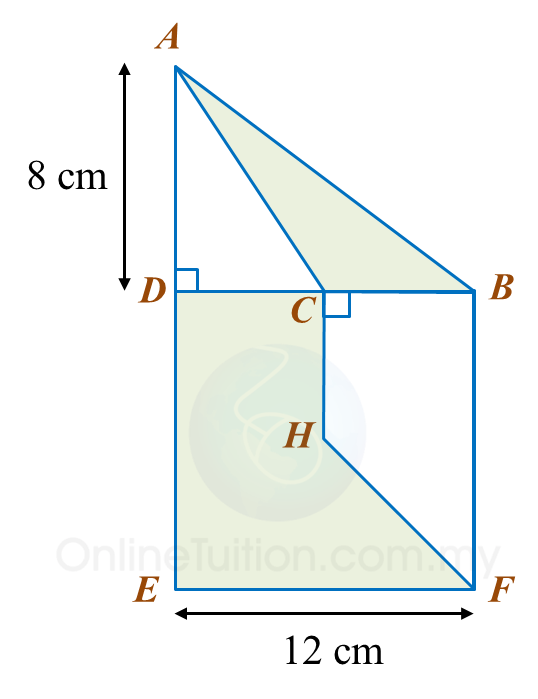
In diagram below, ADB is a right-angled triangle and DBFE is a square. C is the midpoint of DB and CH = CD.
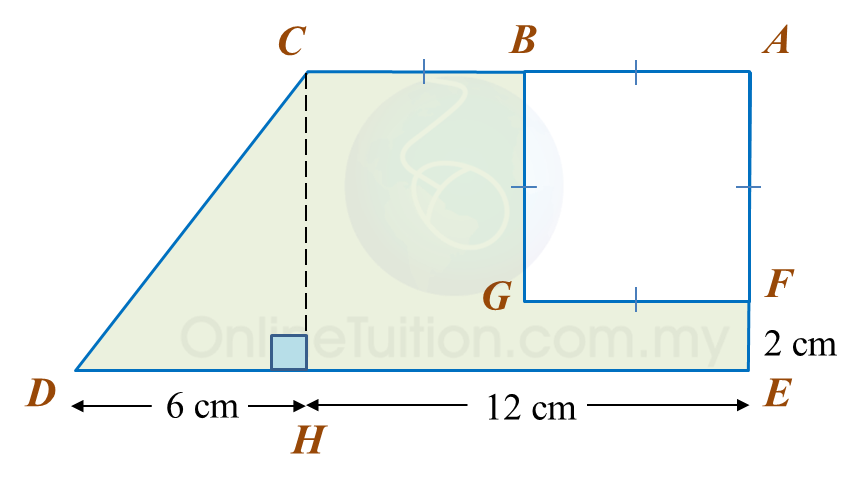
 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
Solution:
Area of △ ABC=12×6×8=24 cm2Area of trapezium BCHF=12×(12+6)×6=54 cm2Area of CDEFH=(12×12)−54=144−54=90 cm2Area of coloured region=24+90=114 cm2
In diagram below, ADB is a right-angled triangle and DBFE is a square. C is the midpoint of DB and CH = CD.
 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.Solution:
Area of △ ABC=12×6×8=24 cm2Area of trapezium BCHF=12×(12+6)×6=54 cm2Area of CDEFH=(12×12)−54=144−54=90 cm2Area of coloured region=24+90=114 cm2
Question 10:
Diagram below shows a rectangle ACDE.
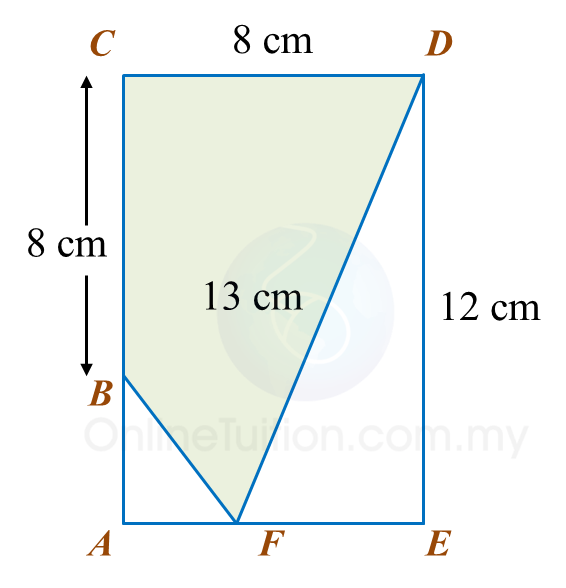
Calculate the area, in cm2, of the coloured region.
Solution:
Using Pythagoras' theorem (Refer Form 2 Chapter 6)FE2=DF2−DE2 =132−122 =169−144 =25FE=√25=5 cmAF=8−5=3 cmAB=12−8=4 cmArea of rectangle ACDE=8×12=96 cm2Area of △ ABF=12×3×4=6 cm2Area of △ DEF=12×5×12=30 cm2Area of coloured region=96−30−6=60 cm2
Diagram below shows a rectangle ACDE.

Calculate the area, in cm2, of the coloured region.
Solution:
Using Pythagoras' theorem (Refer Form 2 Chapter 6)FE2=DF2−DE2 =132−122 =169−144 =25FE=√25=5 cmAF=8−5=3 cmAB=12−8=4 cmArea of rectangle ACDE=8×12=96 cm2Area of △ ABF=12×3×4=6 cm2Area of △ DEF=12×5×12=30 cm2Area of coloured region=96−30−6=60 cm2
Question 11:
Diagram below shows a sketch of parallelogram shaped garden, PQRS that consists of flower beds and a playground.
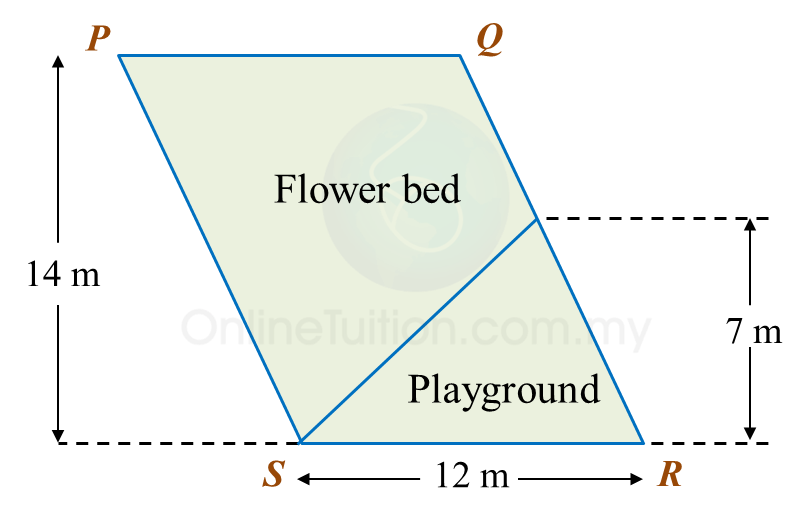 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.
Solution:
Area flower bed=(12×14)−(12×12×7)=168−42=126 m2
Diagram below shows a sketch of parallelogram shaped garden, PQRS that consists of flower beds and a playground.
 Calculate the area, in m2, of the flower beds.
Calculate the area, in m2, of the flower beds.Solution:
Area flower bed=(12×14)−(12×12×7)=168−42=126 m2
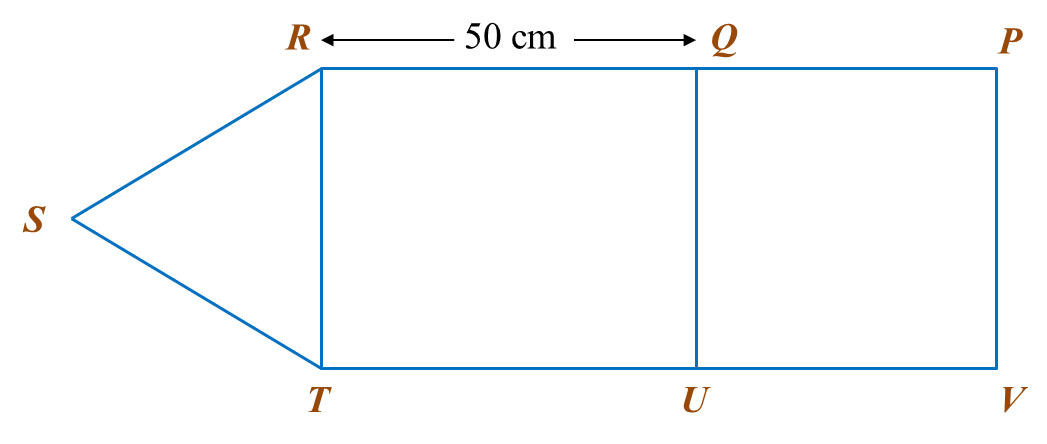
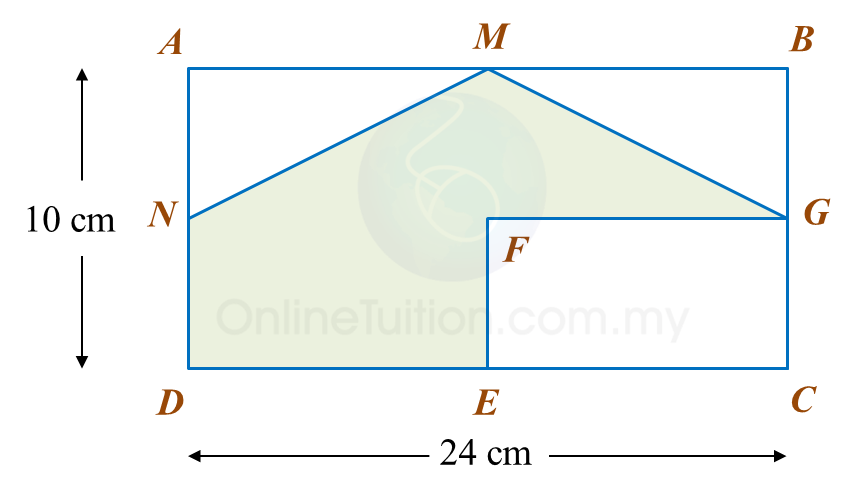
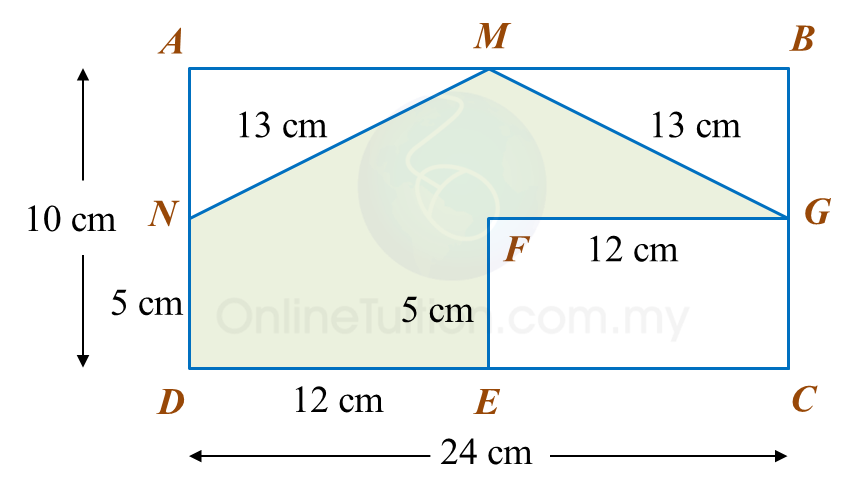
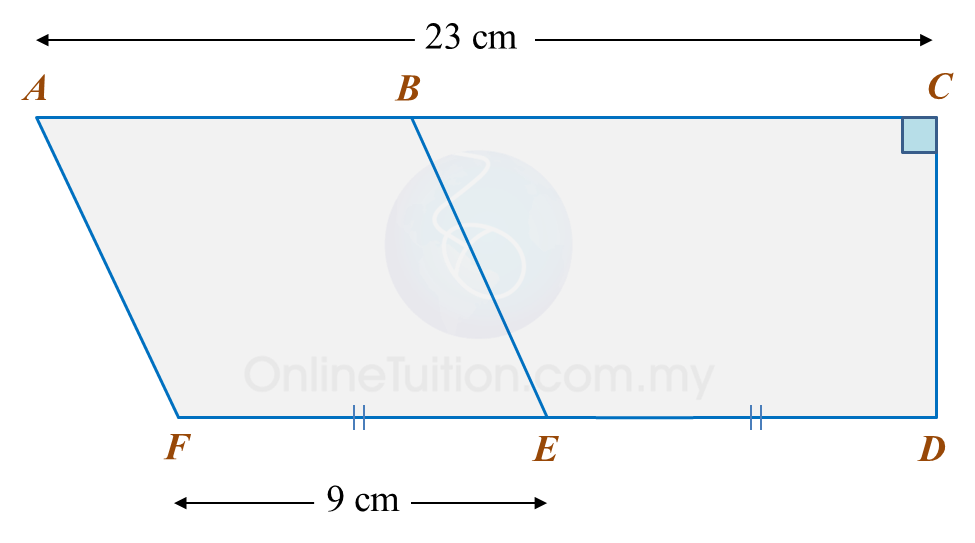 The area of ABEF is 72 cm2.
The area of ABEF is 72 cm2.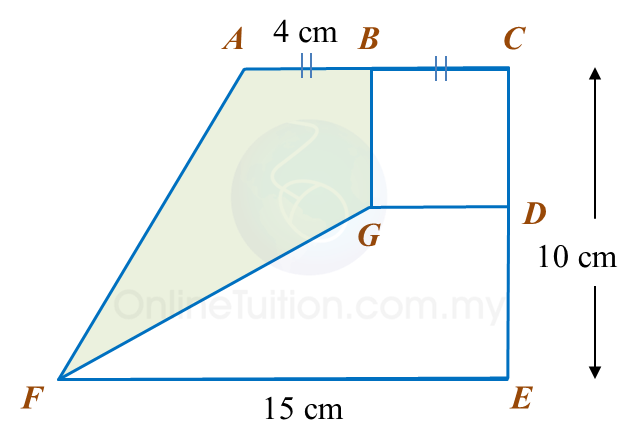
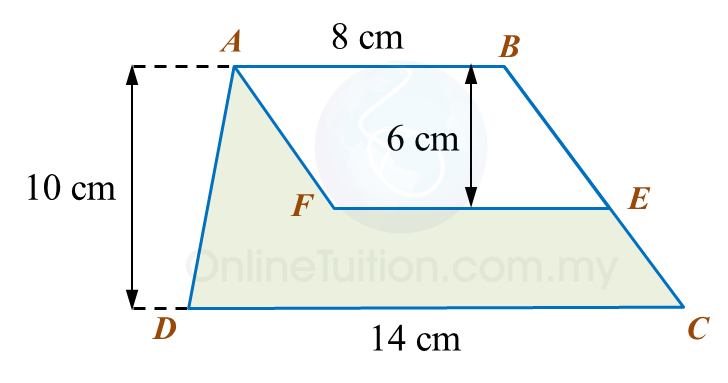 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
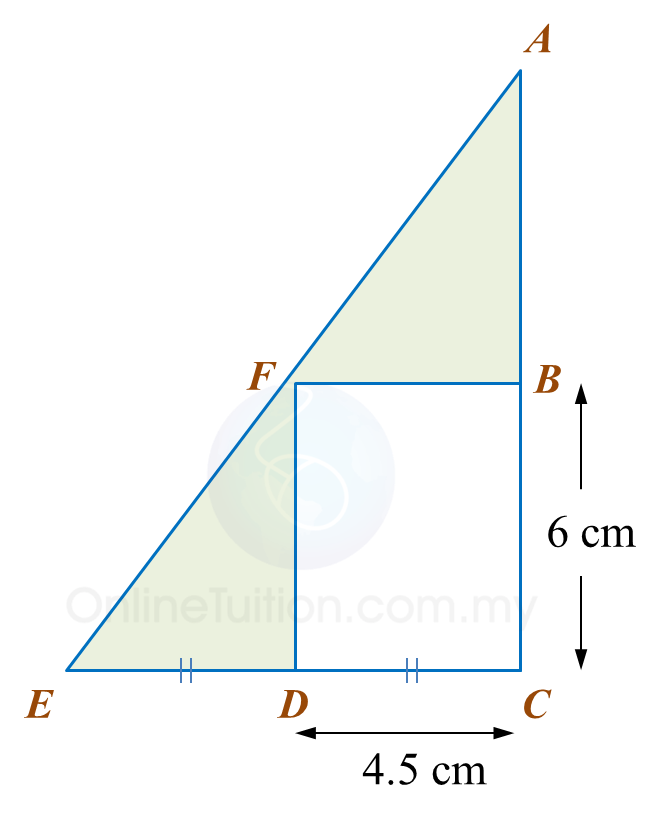 Calculate
Calculate