Question 10:
Diagram below shows the distance from Town P to Town Q and Town Q to Town R.
 (a) Rahim rode his bicycle from Town P at 9.00 a.m. and took 2 hours to reach Town Q.
(a) Rahim rode his bicycle from Town P at 9.00 a.m. and took 2 hours to reach Town Q.
What is the speed, in km/h, of the bicycle?
(b) Rahim took 30 minutes rest at Town Q and continued his journey to Town R three times faster than his earlier speed.
State the time he reached Town R.
Solution:
(a)
The speed of the bicycle from Town P to Town Q=DistanceTime=102=5 km/h
(b)
Speed=DistanceTimeRahim took 30 minutes rest at Town Q.Time taken when his journey to Town R three timesfaster than his earlier speed.=255×3=53=123 hours=1 hour 40 minutes ←23×60=40 minutesTotal time taken from Town P to Town Q and Town Q to Town R=2 hours +30 minutes+1 hour 40 minutes=4 hour 10 minutesThe time he reached Town R at 1.10 p.m.

Diagram below shows the distance from Town P to Town Q and Town Q to Town R.
 (a) Rahim rode his bicycle from Town P at 9.00 a.m. and took 2 hours to reach Town Q.
(a) Rahim rode his bicycle from Town P at 9.00 a.m. and took 2 hours to reach Town Q.What is the speed, in km/h, of the bicycle?
(b) Rahim took 30 minutes rest at Town Q and continued his journey to Town R three times faster than his earlier speed.
State the time he reached Town R.
Solution:
(a)
The speed of the bicycle from Town P to Town Q=DistanceTime=102=5 km/h
(b)
Speed=DistanceTimeRahim took 30 minutes rest at Town Q.Time taken when his journey to Town R three timesfaster than his earlier speed.=255×3=53=123 hours=1 hour 40 minutes ←23×60=40 minutesTotal time taken from Town P to Town Q and Town Q to Town R=2 hours +30 minutes+1 hour 40 minutes=4 hour 10 minutesThe time he reached Town R at 1.10 p.m.

Question 11:
Diagram below shows a trailer travelling from a factory to location P and location P to location Q. The trailer departs at 8.00 a.m.



(a) Based on the Table, calculate the total mass, in tonne, of the trailer and its load.
(b) The trailer arrived at location P at 10.00 a.m. and it stopped for 1½ hours to unload half of the concrete pipes. The trailer then continued its journey to location Q two times faster than its earlier speed. State the time, the trailer reached at location Q.
Solution:
(a)
Mass of concrete pipe on the trailer=500 kg×8=4000 kg=40001000=4 tonnesTotal mass of the trailer and its load=1.5+4.0=5.5 tonnes
(b)
Speed=DistanceTimeTime taken to travel from the Factory to Location P=10.00 a.m.−8.00 a.m.=2 hoursSpeed of the trailer=802=40 km/hIt stopped for 112 hours to unload half of the concrete pipes.Time taken to continue its journey to Location Q=DistanceSpeed=20040×2=212 hoursThe time the trailer reached at Location Q=1400 hours or 2.00 p.m.

Diagram below shows a trailer travelling from a factory to location P and location P to location Q. The trailer departs at 8.00 a.m.



(a) Based on the Table, calculate the total mass, in tonne, of the trailer and its load.
(b) The trailer arrived at location P at 10.00 a.m. and it stopped for 1½ hours to unload half of the concrete pipes. The trailer then continued its journey to location Q two times faster than its earlier speed. State the time, the trailer reached at location Q.
Solution:
(a)
Mass of concrete pipe on the trailer=500 kg×8=4000 kg=40001000=4 tonnesTotal mass of the trailer and its load=1.5+4.0=5.5 tonnes
(b)
Speed=DistanceTimeTime taken to travel from the Factory to Location P=10.00 a.m.−8.00 a.m.=2 hoursSpeed of the trailer=802=40 km/hIt stopped for 112 hours to unload half of the concrete pipes.Time taken to continue its journey to Location Q=DistanceSpeed=20040×2=212 hoursThe time the trailer reached at Location Q=1400 hours or 2.00 p.m.

Question 12:
Diagram below shows travel information of Jason and Mary from Town A to Town B. Jason drives a lorry while Mary drives a car.
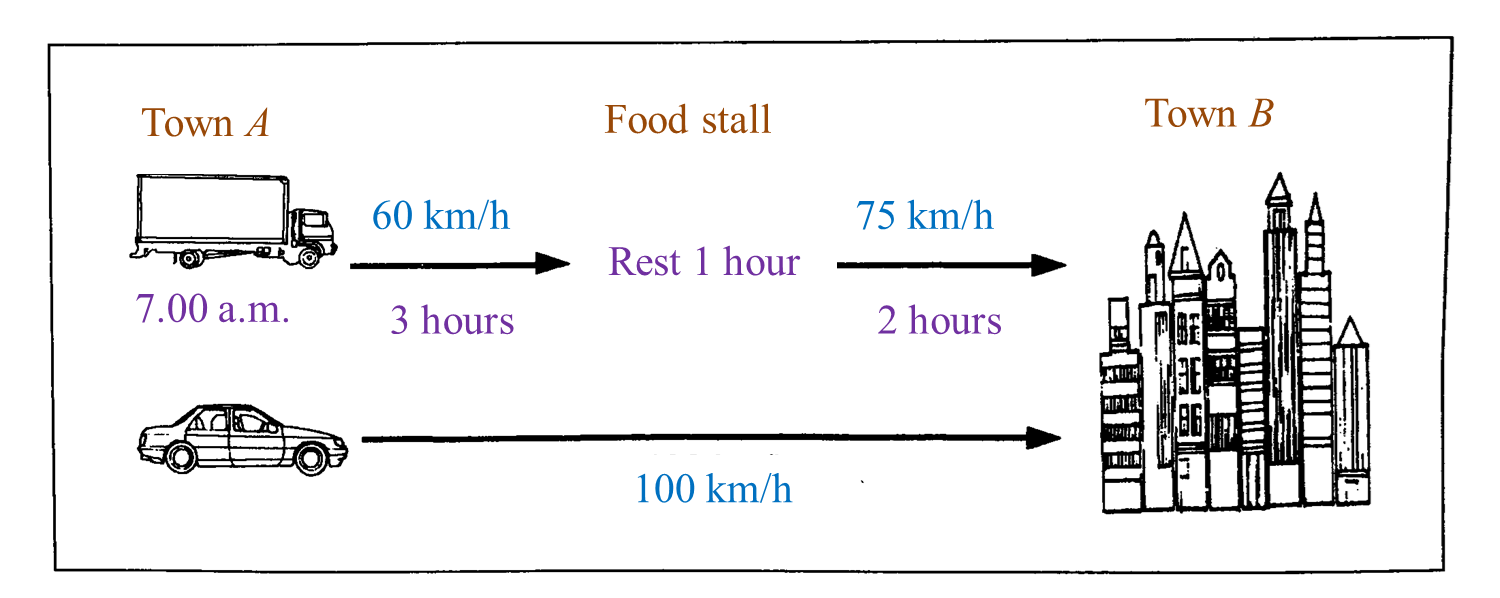
(a) Jason started his journey from Town A at 7.00 a.m.
State the time, Jason reached at Town B.
(b) If both of them reached Town B at the same time, state the time Mary started her journey from Town A.
Solution:
(a)
Total time taken from Town A to Town B
= 3 hours + 1 hour + 2 hours
= 6 hours
Time Jason reached Town B
= 0700 + 0600
= 1300 hours → 1.00 p.m.
(b)
Speed=DistanceTimeTotal distance from Town A to Town B=(60×3)+(75×2)=180+150=330 kmTime taken by Mary=330100=3.3 hours=3 hours 18 minutes ←0.3×60=18 minutesThe time Mary started her journey from Town A=9.42 a.m.
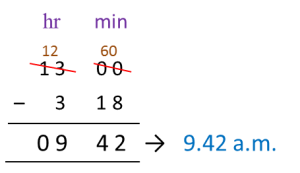
Diagram below shows travel information of Jason and Mary from Town A to Town B. Jason drives a lorry while Mary drives a car.

(a) Jason started his journey from Town A at 7.00 a.m.
State the time, Jason reached at Town B.
(b) If both of them reached Town B at the same time, state the time Mary started her journey from Town A.
Solution:
(a)
Total time taken from Town A to Town B
= 3 hours + 1 hour + 2 hours
= 6 hours
Time Jason reached Town B
= 0700 + 0600
= 1300 hours → 1.00 p.m.
(b)
Speed=DistanceTimeTotal distance from Town A to Town B=(60×3)+(75×2)=180+150=330 kmTime taken by Mary=330100=3.3 hours=3 hours 18 minutes ←0.3×60=18 minutesThe time Mary started her journey from Town A=9.42 a.m.


