12.2.2 Solid Geometry (II), PT3 Focus Practice
Question 5:
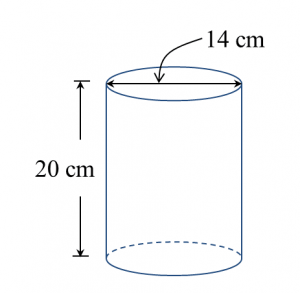
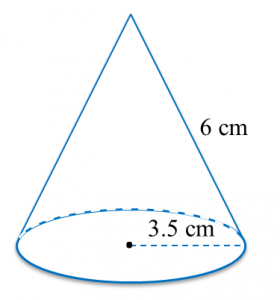
Sphere below has a surface area of 221.76 cm2.

Calculate its radius.
(π=227)
Solution:
Surface area of sphere = 4πr2
4πr2=221.764×227×r2=221.76r2=221.76×74×22r2=17.64r=√17.64r=4.2cm
Question 5:
Sphere below has a surface area of 221.76 cm2.

Calculate its radius.
(π=227)
Solution:
Surface area of sphere = 4πr2
4πr2=221.764×227×r2=221.76r2=221.76×74×22r2=17.64r=√17.64r=4.2cm
Question 6:
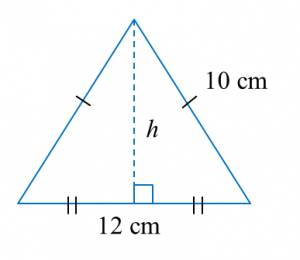
Diagram below shows a right pyramid with a square base.

Given the height of the pyramid is 4 cm.
Calculate the total surface area, in cm2, of the right pyramid.
Solution:
 h2 = 32 + 42
h2 = 32 + 42
= 9 + 16
= 25
h = √25 = 5 cm2
Total surface area of the right pyramid
= Base area + 4 (Area of triangle)
= (6 × 6) + 4 × 4 (½ × 6 × 5)
= 36 + 60
= 96 cm2
Diagram below shows a right pyramid with a square base.

Given the height of the pyramid is 4 cm.
Calculate the total surface area, in cm2, of the right pyramid.
Solution:
 h2 = 32 + 42
h2 = 32 + 42 = 9 + 16
= 25
h = √25 = 5 cm2
Total surface area of the right pyramid
= Base area + 4 (Area of triangle)
= (6 × 6) + 4 × 4 (½ × 6 × 5)
= 36 + 60
= 96 cm2
Question 7:
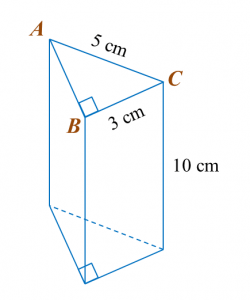
Diagram below shows a prism.

Draw to full scale, the net of the prism on the grid in the answer space. The grid has equal squares with sides of 1 unit.
Solution:
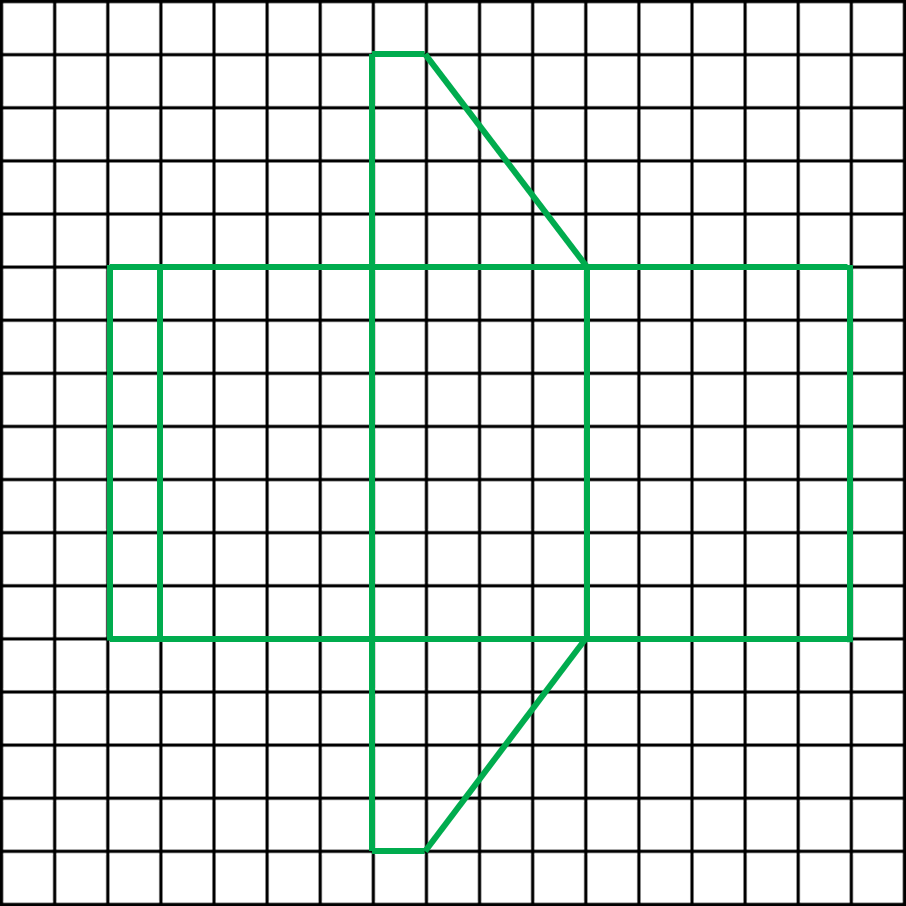
Diagram below shows a prism.

Draw to full scale, the net of the prism on the grid in the answer space. The grid has equal squares with sides of 1 unit.
Solution: