Question 10 (4 marks):
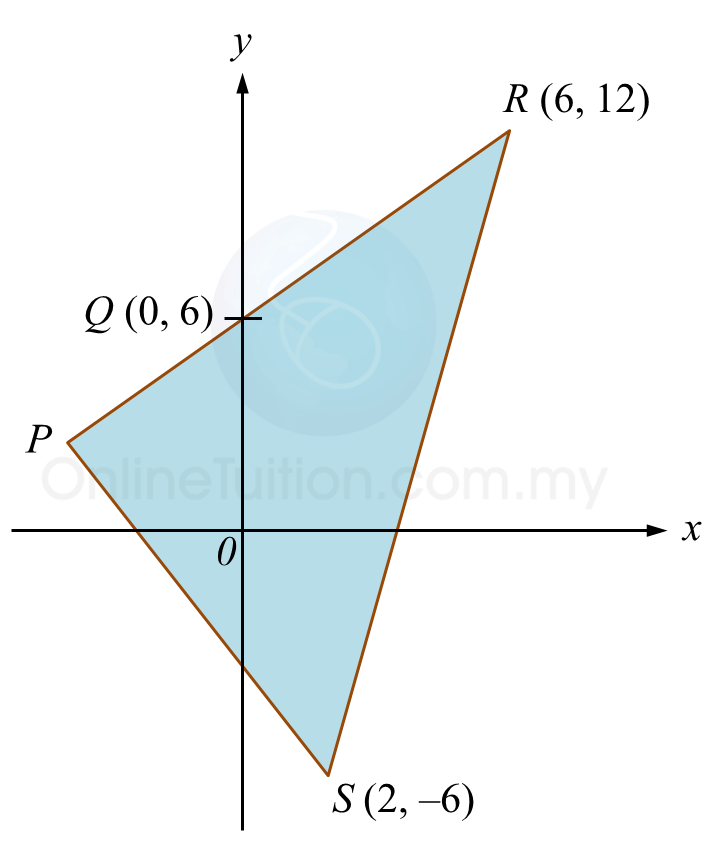
Diagram 10 shows the position of three campsites A, B and C at a part of a riverbank drawn on a Cartesian plane, such that A and B lie on the same straight riverbank.

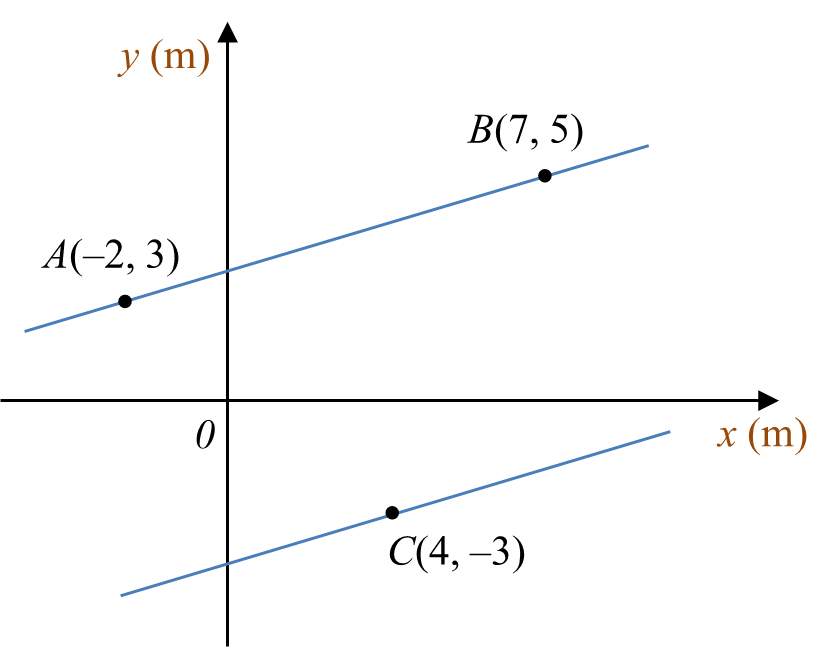Diagram 10

Sam wants to cross the river from campsite C to the opposite riverbank where the campsites A and B are located.
Find the shortest distance, in m, that he can take to cross the river. Give your answer correct to four decimal places.

Solution:

$\begin{array}{l}\text{Let the shortest distance from campsite }C\\ \text{to opposite riverbank is }CD\text{.}\\ \text{Area of }△ABC\\ =\frac{1}{2}|\begin{array}{l}-2\text{ 7 4 }\\ \text{ 3 }5-\text{3 }\end{array}\begin{array}{l}-2\\ \text{ 3}\end{array}|\\ =\frac{1}{2}|\left(-2\right)\left(5\right)+\left(7\right)\left(-3\right)+\left(4\right)\left(3\right)\\ -\left(3\right)\left(7\right)-\left(5\right)\left(4\right)-\left(-3\right)\left(-2\right)|\\ =\frac{1}{2}|-66|\\ =33{\text{ units}}^2\\ \\ \text{Distance of }AB\\ =\sqrt{{\left(-2-7\right)}^2+{\left(3-5\right)}^2}\\ =\sqrt{85}\text{ m}\\ \\ \text{Area of }△ABC=33\\ \frac{1}{2}\left(AB\right)\left(CD\right)=33\\ \frac{1}{2}\left(\sqrt{85}\right)\left(CD\right)=33\\ CD=\frac{33\left(2\right)}{\sqrt{85}}\\ CD=7.1587\left(4\text{ d}\text{.p}\text{.}\right)\\ \\ \text{Thus, the shortest distance is 7}\text{.1587 m}\text{.}\end{array}$

Question 8 (3 marks):
The following information refers to the equation of two straight lines, AB and CD.

$\boxed{\begin{array}{l}AB:y-2kx-3=0\\ CD:\frac{x}{3h}+\frac{y}{4}=1\\ \\ \text{where }h\text{ and }k\text{ are constants}\text{.}\end{array}}$

Given the straight lines AB and CD are perpendicular to each other, express h in terms of k.

Solution:
$\begin{array}{l}AB:y-2kx-3=0\\ y=2kx+3\\ m_{AB}=2k\\ \\ CD:\frac{x}{3h}+\frac{y}{4}=1\\ m_{CD}=-\frac{4}{3h}\\ \\ m_{AB}\times m_{CD}=-1\\ 2k\times \left(-\frac{4}{3h}\right)=-1\\ -8k=-3h\\ h=\frac{8}{3}k\end{array}$

Question 9 (3 marks):
A straight line passes through P(3, 1) and Q(12, 7). The point R divides the line segment PQ such that 2PQ = 3RQ.
Find the coordinates of R.

Solution:



$\begin{array}{l}2PQ=3RQ\\ \frac{PQ}{RQ}=\frac{3}{2}\\ \\ \text{Point }R\\ =\left(\frac{1\left(12\right)+2\left(3\right)}{1+2},\frac{1\left(7\right)+2\left(1\right)}{1+2}\right)\\ =\left(\frac{18}{3},\frac{9}{3}\right)\\ =\left(6,3\right)\end{array}$

Question 10 (7 marks):
Solution by scale drawing is not accepted.
Diagram shows the locations of town M and town N drawn on a Cartesian plane.


PQ is a straight road such that the distance from town M and town N to any point on the road is always equal.
(a) Find the equation of PQ.

(b) Another straight road, ST with an equation y = 2x + 7 is to be built.
(i) A traffic light is to be installed at the crossroads of the two roads.
Find the coordinates of the traffic light.
(ii) Which of the two roads passes through town L $\left(-\frac{4}{3},1\right)?$

Solution:
(a)
$\begin{array}{l}T\left(x,y\right)\text{ is a point on }PQ.\\ TM=TN\\ \sqrt{\left[x-{\left(-4\right)}^2\right]+{\left[y-\left(-1\right)\right]}^2}=\sqrt{{\left(x-2\right)}^2+{\left(y-1\right)}^2}\\ \sqrt{{\left(x+4\right)}^2+{\left(y+1\right)}^2}=\sqrt{{\left(x-2\right)}^2+{\left(y-1\right)}^2}\\ {\left(x+4\right)}^2+{\left(y+1\right)}^2={\left(x-2\right)}^2+{\left(y-1\right)}^2\\ x^2+8x+16+y^2+2y+1\\ =x^2-4x+4+y^2-2y+1\\ 8x+2y+17+4x+2y-5=0\\ 12x+4y+12=0\\ 3x+y+3=0\\ \\ \text{Equation of }PQ:3x+y+3=0\end{array}$


(b)(i)
$\begin{array}{l}y=2x+7\mathrm{............}\left(1\right)\\ 3x+y+3=0\mathrm{............}\left(2\right)\\ \text{Substitute }\left(1\right)\text{ into }\left(2\right):\\ 3x+2x+7+3=0\\ 5x=-10\\ x=-2\\ \\ \text{When }x=-2,\\ From\left(1\right),\\ y=2\left(-2\right)+7=3\\ \text{Coordinates of traffic light}=\left(-2,3\right).\end{array}$


(b)(ii)
$\begin{array}{l}L\left(-\frac{4}{3},1\right):x=-\frac{4}{3},y=1\\ \text{The equation of }ST:y=2x+7\\ \text{Left hand side: }y=1\\ \text{Right hand side: }2\left(-\frac{4}{3}\right)+7=4\frac{1}{3}\\ \text{Thus, the road }y=2x+7\text{ does not }\\ \text{pass through }L\text{.}\\ \\ \text{The equation of }PQ:3x+y+3=0\\ \text{Left hand side: }\\ 3x+y+3=3\left(-\frac{4}{3}\right)+1+3\\ =-4+4=0\\ \text{Right hand side}=0\\ \text{Left hand side}=\text{Right hand side}\\ \\ \text{Thus, the road }3x+y+3=0\\ \text{passes through }L\text{.}\end{array}$

Question 9 (6 marks):
Solution by scale drawing is not accepted.
Diagram shows a triangle OCD.
Diagram

(a) Given the area of triangle OCD is 30 units², find the value of h.

(b) Point Q (2, 4) lies on the straight line CD.
(i) Find CQ : QD.
(ii) Point P moves such that PD = 2 PQ.
  Find the equation of the locus P.

Solution:
(a)
$\begin{array}{l}\text{Given Area of }△OCD\text{ = }30\\ \\ \frac{1}{2}|\begin{array}{l}\text{0 }h-6\\ \text{0 2 8 }\end{array}\begin{array}{l}0\\ 0\end{array}|=30\\ \\ |\left(0\right)\left(2\right)+\left(h\right)\left(8\right)+\left(-6\right)\left(0\right)-\left(0\right)\left(h\right)-\left(2\right)\left(-6\right)-\left(8\right)\left(0\right)|=60\\ |0+8h+0-0+12-0|=60\\ |8h+12|=60\\ \\ 8h+12=60\\ 8h=48\\ h=6\\ \text{or }\\ 8h+12=-60\\ 8h=-72\\ h=-9\left(\text{ignore}\right)\end{array}$


(b)(i)

$\begin{array}{l}\left[\frac{6\left(m\right)+\left(-6\right)\left(n\right)}{m+n},\frac{2\left(m\right)+\left(8\right)\left(n\right)}{m+n}\right]=\left(2,4\right)\\ \frac{6m-6n}{m+n}=2\\ 6m-6n=2m+2n\\ 4m=8n\\ \frac{m}{n}=\frac{8}{4}\\ \frac{m}{n}=\frac{2}{1}\\ \\ \frac{2m+8n}{m+n}=4\\ 2m+8n=4m+4n\\ 2m=4n\\ \frac{m}{n}=\frac{4}{2}\\ \frac{m}{n}=\frac{2}{1}\\ \\ \text{Thus, }CQ=QD=2:1\end{array}$


(b)(ii)
$\begin{array}{l}PD=2PQ\\ \sqrt{{\left(x-6\right)}^2+{\left(y-2\right)}^2}=2\sqrt{{\left(x-2\right)}^2+{\left(y-4\right)}^2}\\ {\left(x-6\right)}^2+{\left(y-2\right)}^2=4\left[{\left(x-2\right)}^2+{\left(y-4\right)}^2\right]\\ x^2-12x+36+y^2-4y+4=4\left[x^2-4x+4+y^2-8y+16\right]\\ x^2-12x+36+y^2-4y+4=4x^2-16x+16+4y^2-32y+64\\ \text{The equation of locus }P:\\ 3x^2+3y^2-4x-28y+40=0\end{array}$

Question 7:
Solution:
$\begin{array}{l}\frac{x}{12}+\frac{y}{-6}=1\\ \frac{x}{12}-\frac{y}{6}=1\end{array}$

(b)
$\begin{array}{l}\text{Given }2RQ=QS\\ \frac{RQ}{QS}=\frac{1}{2}\\ \text{Lets coordinates of }Q=(x,y)\\ \left(\frac{\left(0\right)\left(2\right)+\left(12\right)\left(1\right)}{1+2},\frac{\left(-6\right)\left(2\right)+\left(0\right)\left(1\right)}{1+2}\right)=\left(x,y\right)\\ x=\frac{12}{3}=4\\ y=-\frac{12}{3}=-4\\ Q=(4,-4)\end{array}$

(c) 
$\begin{array}{l}\text{Gradient of }RS,m_{RS}\\ =-\left(\frac{-6}{12}\right)=\frac{1}{2}\\ \\ m_{PQ}=-\frac{1}{m_{RS}}=-\frac{1}{\frac{1}{2}}=-2\end{array}$

Question 8:

Solution:

Question 7:
Solution:
(a)
$\begin{array}{l}\text{The equation of the locus }Y(x,y)\text{ is given by }YS=5\text{ units}\\ \sqrt{{\left(x-5\right)}^2+{\left(y-3\right)}^2}=5\\ x^2-10x+25+y^2-6y+9=25\\ x^2+y^2-10x-6y+9=0\end{array}$

Question 5:
Diagram below shows a quadrilateral ABCD. Point C lies on the y-axis.

The equation of a straight line AD is 2y = 5x – 21
(a) Find
(i) the equation of the straight line AB,
(ii) the coordinates of A,
(b) A point P moves such that its distance from point D is always 5 units.
Find the equation of the locus of P.

Solution:
(a)(i)
$\begin{array}{l}2y=5x-21\\ y=\frac{5}{2}x-\frac{21}{2}\\ m_{AD}=\frac{5}{2}\\ m_{AB}\times m_{AD}=-1\\ m_{AB}\times \frac{5}{2}=-1\\ m_{AB}=-\frac{2}{5}\\ \\ \text{Equation of }AB\\ y-y_1=m_{AB}\left(x-x_1\right)\\ y+1=-\frac{2}{5}\left(x+2\right)\\ 5y+5=-2x-4\\ 5y=-2x-9\end{array}$

(a)(ii)
$\begin{array}{l}2y=5x-21\mathrm{..........}\left(1\right)\\ 5y=-2x-9\mathrm{..........}\left(2\right)\\ \left(1\right)\times 5:10y=25x-105\mathrm{..........}\left(3\right)\\ \left(2\right)\times 2:10y=-4x-18\mathrm{..........}\left(4\right)\\ \left(2\right)-\left(4\right):0=29x-87\\ x=3\\ \text{From }\left(1\right),\\ 2y=15-21\\ 2y=-6\\ y=-3\\ A=\left(3\text{ , }-3\right)\end{array}$

(b)
$\begin{array}{l}y=2,\\ 4=5x-21\\ 5x=25\\ x=5\\ \text{Point }D=\left(5,2\right)\\ PD=5\\ \sqrt{{\left(x-5\right)}^2+{\left(y-2\right)}^2}=5\\ {\left(x-5\right)}^2+{\left(y-2\right)}^2=25\\ x^2-10x+25+\left(y^2-4y+4\right)=25\\ x^2+y^2-10x-4y+4=0\end{array}$