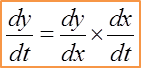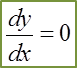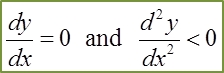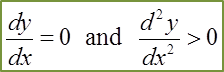Question 20:
Solution:
V=15h3+7hdVdh=35h2+7=3h2+355Given dVdt=15, h=3Rate of change of the height of water=dhdtdhdt=dhdV×dVdt←Chain ruledhdt=53h2+35×15dhdt=7562 cms−1
The volume of water V cm3, in a container is given by
V=15h3+7h
, where h cm is the height of the water in the container. Water is poured into the container at the rate of 15cm3s-1. Find the rate of change of the height of water in cms-1, at the instant when its height is 3cm.
Solution:
V=15h3+7hdVdh=35h2+7=3h2+355Given dVdt=15, h=3Rate of change of the height of water=dhdtdhdt=dhdV×dVdt←Chain ruledhdt=53h2+35×15dhdt=7562 cms−1
Question 21:
Solution:
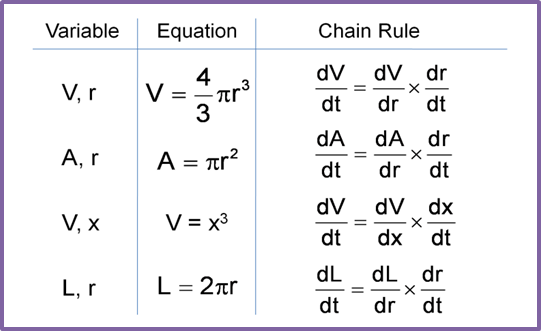
Length of circumference of a circle, L=2πrdLdr=2π
(a)
Given dLdt=0.3Rate of change in the radius of the circle=drdtdrdt=drdL×dLdtdrdt=12π×0.3drdt=0.0477 cms−1
(b)
2πr=88r=882π=44πHence, the radius of the circle after 5s=44π+5(0.0477)=14.24 cm
A wire of length 88 cm is bent to form a circle. When the wire is heated, the length increases at the rate of 0.3 cms-1.
(a) Calculate the rate of change in the radius of the circle.
(b) Hence, calculate the radius of the circle after 5s.
Length of circumference of a circle, L=2πrdLdr=2π
(a)
Given dLdt=0.3Rate of change in the radius of the circle=drdtdrdt=drdL×dLdtdrdt=12π×0.3drdt=0.0477 cms−1
(b)
2πr=88r=882π=44πHence, the radius of the circle after 5s=44π+5(0.0477)=14.24 cm
Question 22:
Solution:
Let, h = height of the water levelr = radius of the water surfaceV = volume of the waterrh=0.40.6←Concept of similar trianglesrh=23r=23hVolume of water, V=13πr2hV=13π(23h)2hV=427πh3dVdh=(3)427πh2dVdh=49πh2The rate of change of the height of the water levelwhen the height of water level is 0.5 m=dhdt.dhdt=dhdV×dVdt←Chain ruledhdt=94πh2×0.02←Given dVdt=0.02dhdt=94π(0.5)2×0.02dhdt=0.0572 ms−1
The diagram shows a conical container with diameter 0.8m and height 0.6m. Water is poured into the container at a constant rate of 0.02m3s-1. Calculate the rate of change of the height of the water level when the height of water level is 0.5m.
Let, h = height of the water levelr = radius of the water surfaceV = volume of the waterrh=0.40.6←Concept of similar trianglesrh=23r=23hVolume of water, V=13πr2hV=13π(23h)2hV=427πh3dVdh=(3)427πh2dVdh=49πh2The rate of change of the height of the water levelwhen the height of water level is 0.5 m=dhdt.dhdt=dhdV×dVdt←Chain ruledhdt=94πh2×0.02←Given dVdt=0.02dhdt=94π(0.5)2×0.02dhdt=0.0572 ms−1