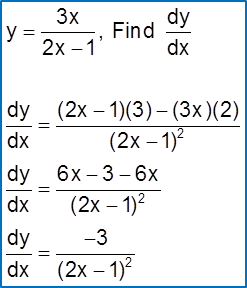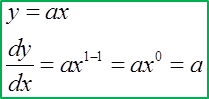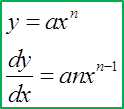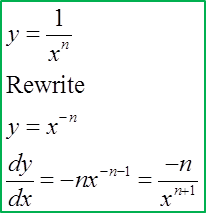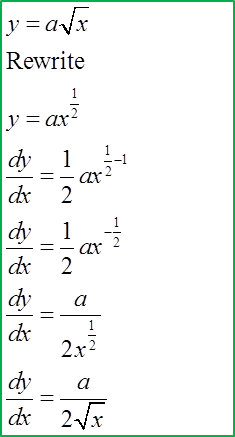Find the Derivatives of a Quotient using Quotient Rule
Method 1: The Quotient Rule
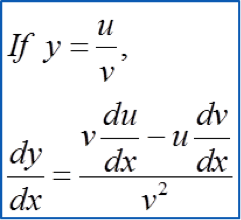
Example:
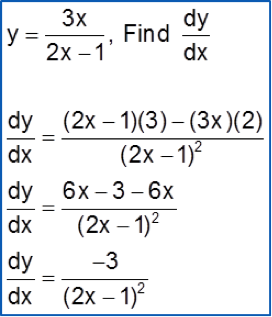
Method 2: (Differentiate Directly)

Example:
Given thaty=x22x+1,finddydx
Solution:
y=x22x+1dydx=(2x+1)(2x)−x2(2)(2x+1)2=4x2+2x−2x2(2x+1)2=2x2+2x(2x+1)2
Practice 1:
Given thaty=4x3(5x+1)3,finddydx
Solution:
y=4x3(5x+1)3dydx=(5x+1)3(12x2)−4x3.3(5x+1)2.5[(5x+1)3]2=(5x+1)3(12x2)−60x3(5x+1)2(5x+1)6=(12x2)(5x+1)2[(5x+1)−5x](5x+1)6=(12x2)(5x+1)2(1)(5x+1)6=12x2(5x+1)4