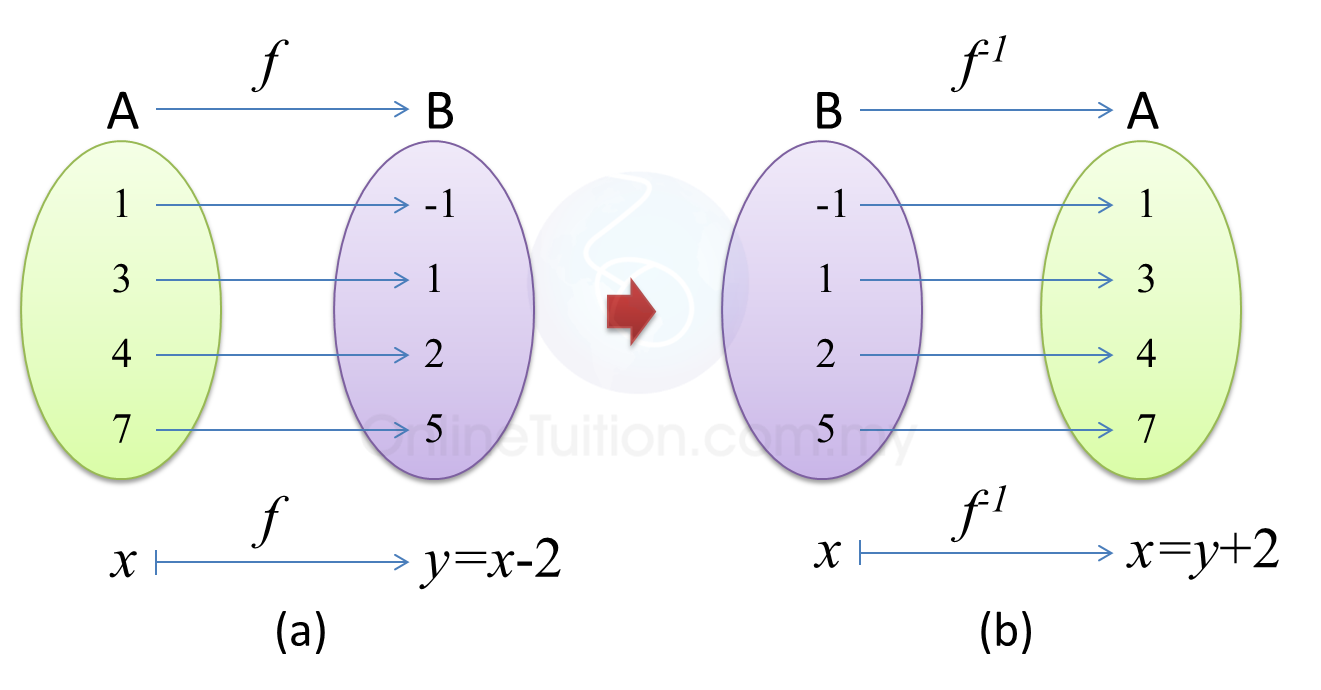
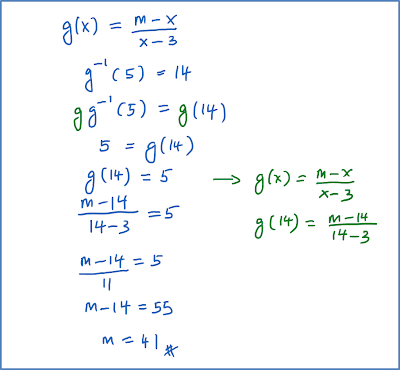Composite Function (Comparison Method) Example 3

Posted on April 18, 2020 by user

Example 3:

Given f: x → hx + k and f² : x → 4x + 15.
(a) Find the values of h and of k.
(b) Take h > 0, find the values of x for which f (x²) = 7x

Solution:

(a)

Step 1:
Find f² (x)

Given f (x) = hx + k

f² (x) = ff (x) = f (hx + k)

= h (hx + k) + k

= h²x + hk + k

Step 2:
Compare with given f² (x)

f² (x) = 4x + 15

h²x + hk+ k = 4x + 15

h²= 4

h = ± 2

When, h = 2

hk + k = 15

2k + k = 15

k = 5

When, h = –2

hk + k = 15

–2k + k = 15

k = –15

(b)

h > 0, h = 2, k = 5

Given f (x) = hx + k

f (x) = 2x + 5

f (x²) = 7x

2 (x²) + 5 = 7x

2x² – 7x+ 5 = 0

(2x – 5)(x–1) = 0

2x – 5 = 0 or x –1= 0

x = 5/2
or
x = 1

Example 1

Posted on April 18, 2020 by user

Example 1

Given the function

f : x \to 6 x + 1

. Find the value of p if

f (4) = 4 p + 5

.

Answer:

\begin{array}{l} f : x \to 6 x + 1 \\ f (x) = 6 x + 1 \\ f (4) = 6 (4) + 1 \\ f (4) = 25 \end{array}

\begin{array}{l} f (4) = 4 p + 5 \\ 25 = 4 p + 5 \\ 4 p = 25 - 5 = 20 \\ p = \frac{20}{4} = 5 \end{array}

SPM Practice (Long Question)

Posted on April 18, 2020 by user

Question 5:
In diagram below, the function g maps set P to set Q and the function h maps set Q to set R.

Find
(a) in terms of x, the function
(i) which maps set Q to set P,
(ii) h(x).
(b) the value of x such that gh(x) = 8x + 1.

Solution:
(a)(i)

\begin{array}{l} g (x) = 3 x + 2 \\ Let g^{- 1} (x) = y \\ g (y) = x \\ 3 y + 2 = x \\ y = \frac{x - 2}{3} \\ g^{- 1} (x) = \frac{x - 2}{3} \end{array}

(a)(ii)

\begin{array}{l} h g (x) = 12 x + 5 \\ h (3 x + 2) = 12 x + 5 \to g (x) = 3 x + 2 \\ Let u = 3 x + 2 \\ x = \frac{u - 2}{3} \\ h (u) = 12 (\frac{u - 2}{3}) + 5 \\ = 4 u - 8 + 5 \\ = 4 u - 3 \\ h (x) = 4 x - 3 \end{array}

(b)

\begin{array}{l} g h (x) = g (4 x - 3) \\ = 3 (4 x - 3) + 2 \\ = 12 x - 9 + 2 \\ = 12 x - 7 \\ 12 x - 7 = 8 x + 1 \\ 4 x = 8 \\ x = 2 \end{array}

Inverse Function Example 7

Posted on April 18, 2020 by user

Example 7 (Comparison Method)
Given that

f : x \to \frac{2 h}{x - 3 k}

, x≠3k , where h and k are constants and

f^{- 1} : x \to \frac{14 + 24 x}{x}

, x≠0, find the value of h and of k.

Solution:

Inverse Function Example 6 (Comparison Method)

Posted on April 18, 2020 by user

Example 6 (Comparison Method)
If

f : x \mapsto \frac{m x - n}{x - 2}, x \neq 2

and

f^{- 1} : x \mapsto \frac{5 - 2 x}{2 - x}, x \neq 2.

. Find the value of m and of n,

Inverse Function Example 5

Posted on April 18, 2020 by user

Example 5

If $g : x \mapsto \frac{m - x}{x - 3}, x \neq 3$ and $g^{- 1} (5) = 14$ . Find the value of m.

Inverse Function Example 3

Posted on April 18, 2020 by user

Example 3
Find the inverse function of

f (x) = \frac{3 x + 2}{5 x + 3}

Inverse Function Example 2

Posted on April 18, 2020 by user

Example 2
Find the inverse function of the following function
(a)

f (x) = \frac{5}{7 x}

(b)

f (x) = \frac{2}{3 - x}

Inverse Function Example 1

Posted on April 18, 2020 by user

Example 1
Find the inverse function of the following function
(a) f(x) = 4 – 7x,
(b)

f (x) = \frac{2 x + 5}{3}

1.4 Inverse Function

Posted on April 18, 2020 by user

Inverse Functions

1. Consider the function (f : x maps to - 2) with domain A = {1, 3, 4, 7}. Then the range of the function is B = {-1, 1, 2, 5}. The arrow diagram representing this function is shown as below.

2. If the arrows of (a) are reversed, the arrow diagram in (b) is obtained. A new function having domain B and range A is formed from the function f. This new function is called the inverse function of f and is denoted by f^-1 .

3. To Find the inverse function,

f^{- 1} (x)

f (x)

• Put the function equal to y.
• Rearrange to give x in term of y.
• Rewrite as

f^{- 1} (x)

replacing y by x.

Example: Given

f (x) = 5 x - 4

, find the inverse function.