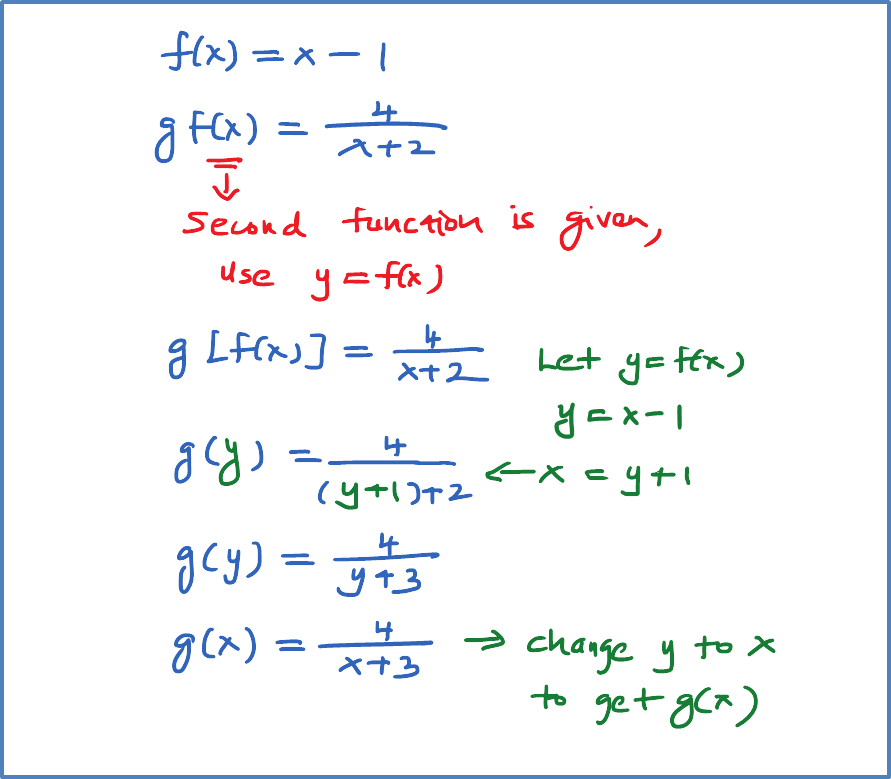Functions
Finding a new function given a composite function (Case B : Second function is given) Example 2
Finding a new function given a composite function (Case B : Second function is given) Example 1
Finding a new function given a composite function (Case A : First function is given) Example 3
Example 3
A function f is defined by f:x↦2x+1 .
Find the function g if fg:x↦5x−2x+5,x≠−5 .
[Note : First function is given]
Click here (check for example 5)
A function f is defined by f:x↦2x+1 .
Find the function g if fg:x↦5x−2x+5,x≠−5 .
[Note : First function is given]
Click here (check for example 5)
Finding a new function given a composite function (Case A : First function is given) Example 2
Example 2
A function f is defined by f:x↦2x .
Find the function g if fg:x↦x2+1 .
[Note : the first function f is given]
Click here (check for example 5)
A function f is defined by f:x↦2x .
Find the function g if fg:x↦x2+1 .
[Note : the first function f is given]
Click here (check for example 5)
Finding a new function given a composite function (Case A : First function is given) Example 1
Example 1
A function f is defined by f:x↦2x+5 .
Find the function g if fg:x↦3x−8 .
[Note : First function f is given]
Click here (check for example 5) to learn more about function
A function f is defined by f:x↦2x+5 .
Find the function g if fg:x↦3x−8 .
[Note : First function f is given]
Click here (check for example 5) to learn more about function
Composite Function (Comparison Method) Example 2
Composite Function (Comparison Method) Example 1
Example 3
Example 2
Given f:x↦1−x and g:x↦px2+q. If the composite function gf is defined by gf:x↦3x2−6x+5, find
- the value of p and of q,
- the value of g2(−1).