Question 6 (10 marks):
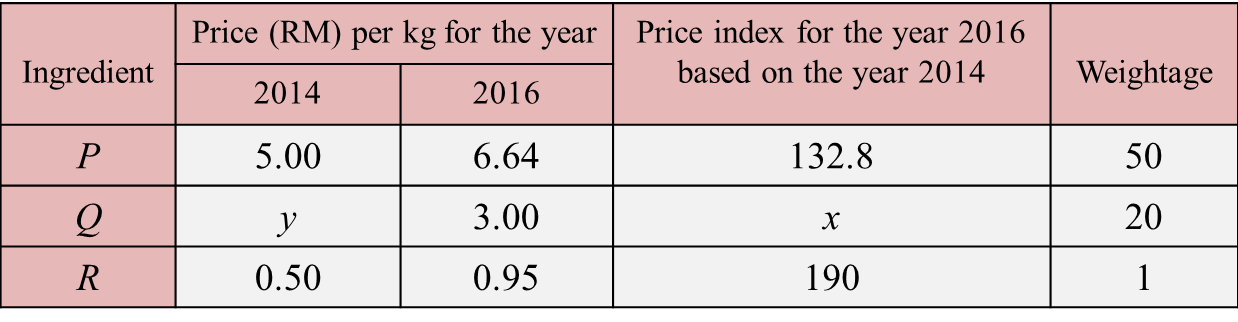
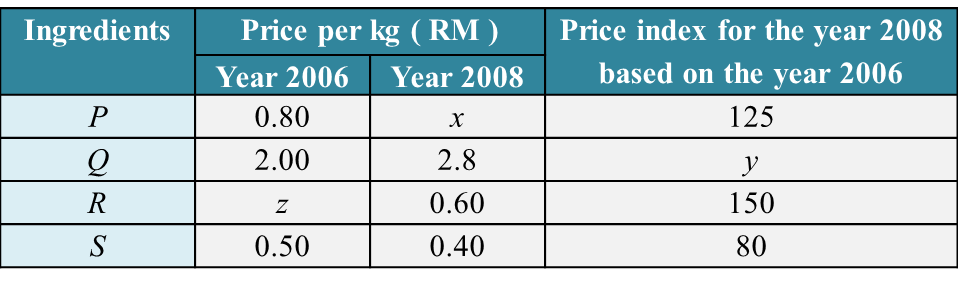
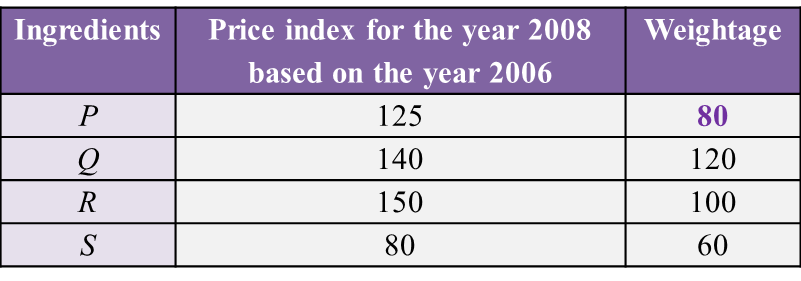
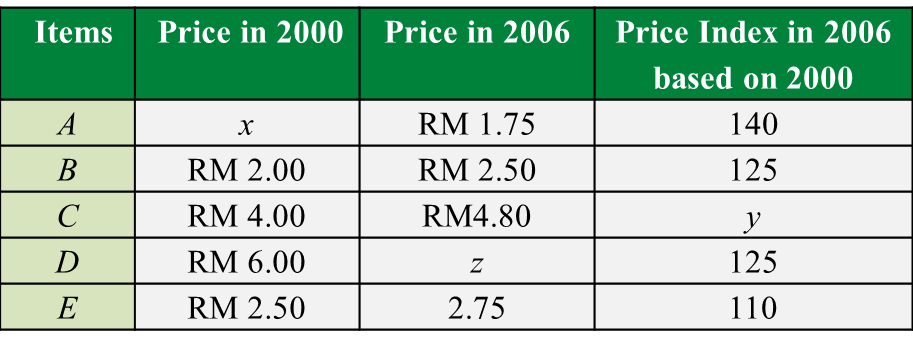
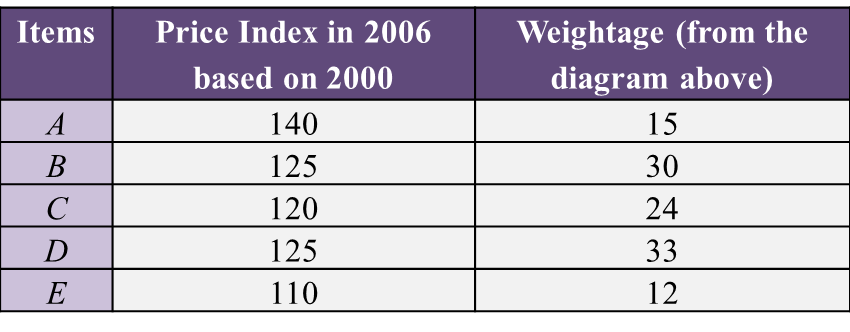
Table 2 shows the information related to four ingredients, J, K, L and M, used in the production of a type of energy drinks.
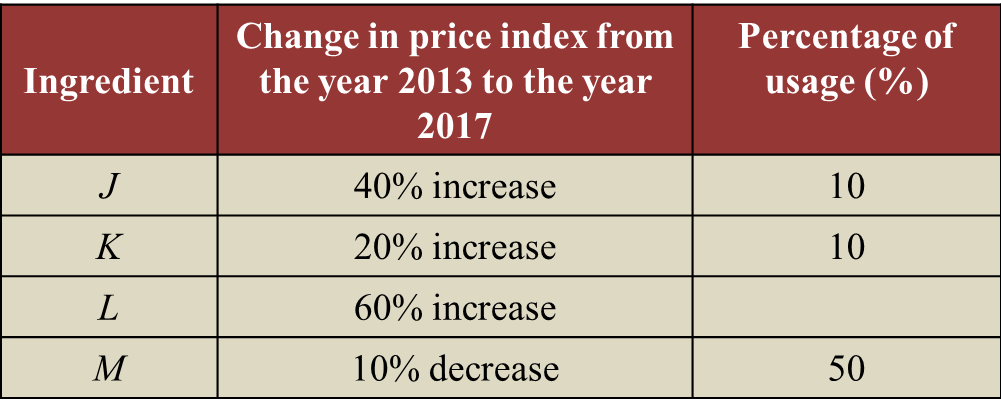
The production cost for this energy drinks is RM47600 in the year 2017.
(a) If the price of ingredient K in the year 2013 is RM4.20, find its price in the year 2017.
(b) Percentage of usage for several ingredients was given in Table 2.
Calculate the corresponding production cost in the year 2013.
(c) The production cost is expected to increase by 50% from the year 2017 to the year 2019.
Calculate the percentage of changes in production cost from the year 2013 to the year 2019.
Solution:
(a)
P2017P2013×100=120P20174.20×100=120P2017=4.20100×120P2017=RM5.04
(b)
Percentage of usage of ingredient L=(100−10−10−50)%=30%Composite index for the production cost inthe year 2017 based on the year 2013, ˉIˉI=∑IW∑WˉI=(140)(10)+(120)(10)+(160)(30)+(90)(50)10+10+30+50ˉI=11900100ˉI=119P2017P2013×100=11947600P2013×100=119P2013=47600×100119P2013=RM40000The production cost in the year 2013 is RM40000.
(c)
year 2013 +19%→ year 2017 +50%→ year 2019∴Expected composite index for the year 2019based on the year 2013, ˉI=119×150100=178.5Percentage of changes=[178.5−100]%=78.5%
Table 2 shows the information related to four ingredients, J, K, L and M, used in the production of a type of energy drinks.

The production cost for this energy drinks is RM47600 in the year 2017.
(a) If the price of ingredient K in the year 2013 is RM4.20, find its price in the year 2017.
(b) Percentage of usage for several ingredients was given in Table 2.
Calculate the corresponding production cost in the year 2013.
(c) The production cost is expected to increase by 50% from the year 2017 to the year 2019.
Calculate the percentage of changes in production cost from the year 2013 to the year 2019.
Solution:
(a)
P2017P2013×100=120P20174.20×100=120P2017=4.20100×120P2017=RM5.04
(b)
Percentage of usage of ingredient L=(100−10−10−50)%=30%Composite index for the production cost inthe year 2017 based on the year 2013, ˉIˉI=∑IW∑WˉI=(140)(10)+(120)(10)+(160)(30)+(90)(50)10+10+30+50ˉI=11900100ˉI=119P2017P2013×100=11947600P2013×100=119P2013=47600×100119P2013=RM40000The production cost in the year 2013 is RM40000.
(c)
year 2013 +19%→ year 2017 +50%→ year 2019∴Expected composite index for the year 2019based on the year 2013, ˉI=119×150100=178.5Percentage of changes=[178.5−100]%=78.5%