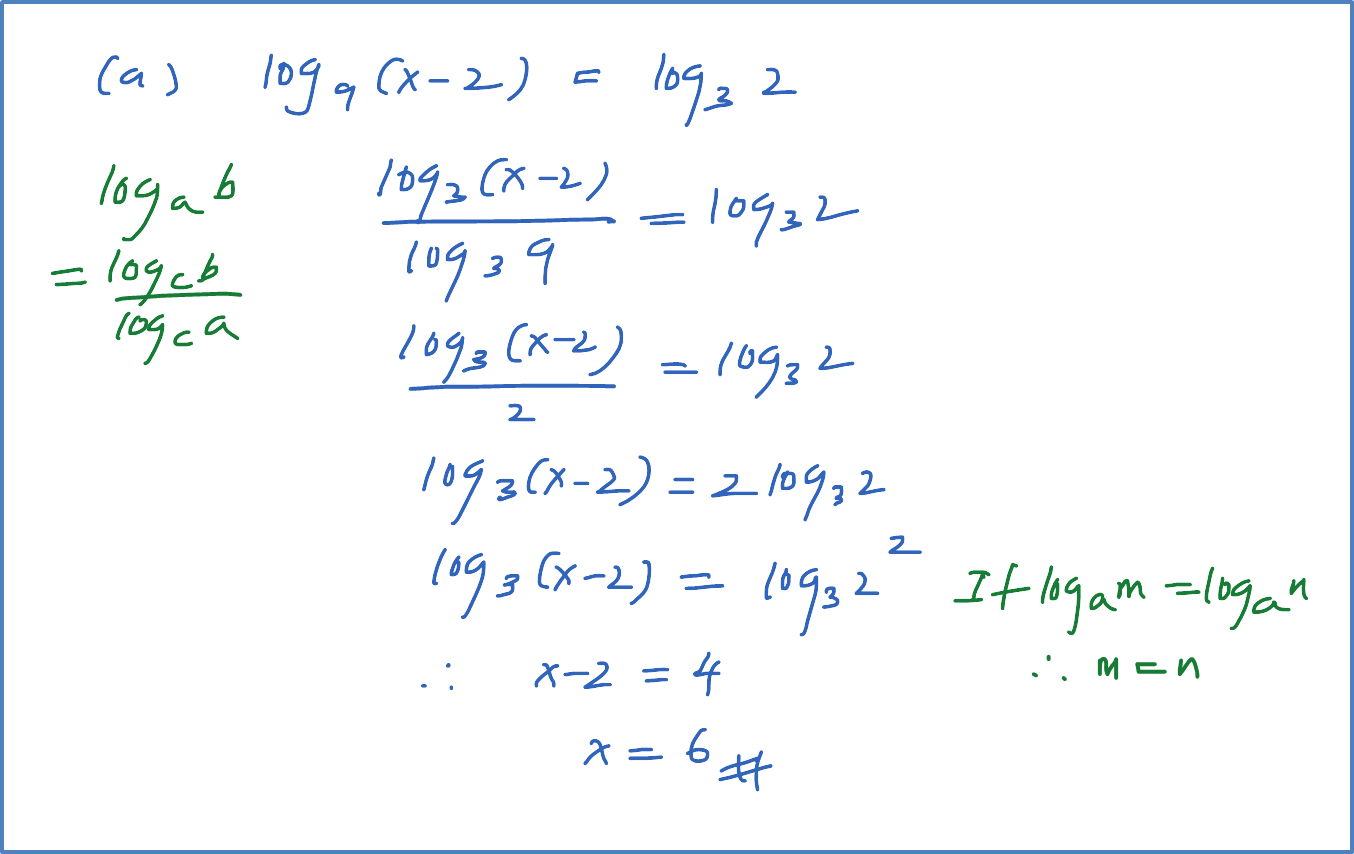Change of Base of Logarithms – Example 5

Posted on May 23, 2020 by Myhometuition

Example 5
Given that

$\log_{2} 3 = 1.585$ and

$\log_{2} 5 = 2.322$ , evaluate the following.
(a)

$\log_{8} 15$
(b)

$\log_{5} 0.6$
(c)

$\log_{15} 30$
(d)

$\log_{16} 45$

Solution:

5.2(a) Example 1 (Logarithms)

Posted on May 22, 2020 by Myhometuition

Example 1
Find the value of each of the following :
(a)

$\log_{2} 64$
(b)

$\log_{3} 1$
(c)

$\log_{5} 5$
(d)

$\log_{\frac{1}{2}} 4$
(e)

$\log_{8} 0.25$

Example 2
Solve the following equations:
(a)

$\log_{3} 5 x = 2$
(b)

$\log_{x + 1} 81 = 2$
(c)

$\log_{x} 5 x - 6 = 2$

Short Questions (Question 15 – 17)

Posted on May 18, 2020 by Myhometuition

Question 15 (4 marks):

$\begin{array}{l} (a) Given P = \log_{a} Q, state the \\ conditions of a . \\ (b) Given \log_{3} y = \frac{2}{\log_{x y} 3}, express \\ y in terms of x . \end{array}$

Solution:
(a)
a > 0, a ≠ 1

(b)

$\begin{array}{l} \log_{3} y = \frac{2}{\log_{x y} 3} \\ \frac{\log_{x y} y}{\log_{x y} 3} = \frac{2}{\log_{x y} 3} \\ \log_{x y} y = 2 \\ y = {(x y)}^{2} \\ y = x^{2} y^{2} \\ \frac{1}{x^{2}} = \frac{y^{2}}{y} \\ y = \frac{1}{x^{2}} \end{array}$

Question 16 (3 marks):

$Given \frac{25^{h + 3}}{125^{p - 1}} =1, express p in terms of h .$

Solution:

$\begin{array}{l} \frac{25^{h + 3}}{125^{p - 1}} = 1 \\ 25^{h + 3} = 125^{p - 1} \\ {(5^{2})}^{h + 3} = {(5^{3})}^{p - 1} \\ 5^{2 h + 6} = 5^{3 p - 3} \\ 2 h + 6 = 3 p - 3 \\ 3 p = 2 h + 9 \\ p = \frac{2 h + 9}{3} \end{array}$

Question 17 (3 marks):

$\begin{array}{l} Solve the equation: \\ \log_{m} 324 - \log_{\sqrt{m}} 2 m = 2 \end{array}$

Solution:

$\begin{array}{l} \log_{m} 324 - \log_{\sqrt{m}} 2 m = 2 \\ \log_{m} 324 - \frac{\log_{m} 2 m}{\log_{m} m^{\frac{1}{2}}} = 2 \\ \log_{m} 324 - 2 (\frac{\log_{m} 2 m}{\log_{m} m}) = 2 \\ \log_{m} 324 - 2 \log_{m} 2 m = 2 \\ \log_{m} 324 - \log_{m} {(2 m)}^{2} = l o g_{m} m^{2} \\ \log_{m} (\frac{324}{4 m^{2}}) = l o g_{m} m^{2} \\ \frac{324}{4 m^{2}} = m^{2} \\ 4 m^{4} = 324 \\ m^{4} = 81 \\ m = \pm 3 (- 3 is rejected) \end{array}$

Long Questions (Question 3 – 4)

Posted on April 21, 2020 by user

5.6.2 Indices and Logarithms, SPM Practice (Long Questions)

Question 3:

Given that p = 3^r and q = 3^t, express the following in terms of r and/ or t.

(a)

$(a) \log_{3} \frac{p q^{2}}{27},$

(b) log₉p – log₂₇ q.

Solution:

(a)

Given p = 3^r, log₃ p = r

q= 3^t, log₃ q =t

$\log_{3} \frac{p q^{2}}{27}$

= log₃ pq² – log₃27

= log₃ p + log₃ q² – log₃ 3³

= r + 2 log₃ q – 3 log₃ 3

= r + 2 log₃ q – 3(1)

= r + 2t – 3

(b)

log₉ p– log₂₇ q

$\begin{array}{l} = \frac{\log_{3} p}{\log_{3} 9} - \frac{\log_{3} q}{\log_{3} 27} \\ = \frac{r}{\log_{3} 3^{2}} - \frac{t}{\log_{3} 3^{3}} \\ = \frac{r}{2 \log_{3} 3} - \frac{t}{3 \log_{3} 3} \\ = \frac{r}{2} - \frac{t}{3} \end{array}$

Question 4:

(a) Simplify:

log₂(2x + 1) – 5 log₄ x²+ 4 log₂ x

(b) Hence, solve the equation:

log₂(2x + 1) – 5 log₄ x²+ 4 log₂ x= 4

Solution:

(a)

log₂ (2x + 1) – 5 log₄ x²+ 4 log₂ x

$\begin{array}{l} = \log_{2} (2 x + 1) - \frac{5 \log_{2} x^{2}}{\log_{2} 4} + 4 \log_{2} x \\ = \log_{2} (2 x + 1) - \frac{5}{2} \log_{2} x^{2} + \log_{2} x^{4} \\ = \log_{2} (2 x + 1) - \log_{2} {(x^{2})}^{(\frac{5}{2})} + \log_{2} x^{4} \end{array}$

$\begin{array}{l} = \log_{2} (2 x + 1) - \log_{2} x^{5} + \log_{2} x^{4} \\ = \log_{2} \frac{(2 x + 1) (x^{4})}{x^{5}} \\ = \log_{2} \frac{2 x + 1}{x} \end{array}$

(b)

log₂ (2x + 1) – 5 log₄ x²+ 4 log₂ x= 4

$\begin{array}{l} \log_{2} \frac{2 x + 1}{x} = 4 \\ \frac{2 x + 1}{x} = 2^{4} \\ \frac{2 x + 1}{x} = 16 \\ 2 x + 1 = 16 x \\ 14 x = 1 \\ x = \frac{1}{14} \end{array}$

Long Questions (Question 1 – 2)

Posted on April 21, 2020 by user

5.6.1 Indices and Logarithms, SPM Practice (Long Questions)

Question 1:

(a) Find the value of

i. 2 log₂ 12 + 3 log₂5 – log₂ 15 – log₂ 150.

ii. log₈32

(b) Shows that 5ⁿ+ 5ⁿ⁺¹+ 5ⁿ⁺²can be divided by 31 for all the values of n which are positive integer.

Solution:

(a)(i)

2 log₂ 12 + 3 log₂ 5 – log₂15 – log₂ 150

= log₂ 12² + log₂ 5³– log₂ 15 – log₂ 150

$= \log_{2} \frac{12^{2} \times 5^{3}}{15 \times 150}$

= log₂ 8

= log₂ 2³

= 3

(a)(ii)

$\begin{array}{l} \log_{8} 32 = \frac{\log_{2} 32}{\log_{2} 8} \\ = \frac{\log_{2} 2^{5}}{\log_{2} 2^{3}} = \frac{5}{3} \end{array}$

(b)

5ⁿ+ 5ⁿ⁺¹+ 5ⁿ⁺²

= 5ⁿ+ (5 × 5ⁿ) + (5² × 5ⁿ)

= 5ⁿ (1 + 5 + 5²)

= 31 × 5ⁿ

Therefore, 5ⁿ+ 5ⁿ⁺¹+ 5ⁿ⁺²can be divided by 31 for all the values of n which are positive integer.

Question 2:

(a) Given log₁₀ x = 3 and log₁₀y = –2. Shows that 2xy – 10000y² = 19.

(b) Solve the equation log₃ x = log₉(x + 6).

Solution:

(a)

log₁₀x = 3 → (x = 10³)

log₁₀y = –2 → (y = 10^-2)

2xy – 10000y² = 19

Left hand side:

2xy – 10000y²

= 2 × 10³× 10^-2– 10000 (10^-2)²

= 20 – 10000 (10^-4)

= 20 – 1

= 19

= right hand side

(b)

$\begin{array}{l} \log_{3} x = \log_{9} (x + 6) \\ \log_{3} x = \frac{\log_{3} (x + 6)}{\log_{3} 9} \\ \log_{3} x = \frac{\log_{3} (x + 6)}{\log_{3} 3^{2}} \\ \log_{3} x = \frac{\log_{3} (x + 6)}{2} \end{array}$

2log₃ x= log₃ (x + 6)

log₃ x²= log₃ (x + 6)

x²= x + 6

x²– x – 6 = 0

(x + 2) (x – 3) = 0

x = – 2 atau 3.

log₃(– 2) not accepted (logarithm of a negative number is undefined)

Jadi, x = 3.

Short Questions (Question 12 – 14)

Posted on April 21, 2020 by user

Question 12

Solve the equation,

$\log_{2} 5 \sqrt{x} + \log_{4} 16 x = 6$

Solution:

$\begin{array}{l} \log_{2} 5 \sqrt{x} + \log_{4} 16 x = 6 \\ \log_{2} 5 \sqrt{x} + \frac{\log_{2} 16 x}{\log_{2} 4} = 6 \\ \log_{2} 5 \sqrt{x} + \frac{\log_{2} 16 x}{2} = 6 \\ 2 \log_{2} 5 \sqrt{x} + \log_{2} 16 x = 12 \\ \log_{2} {(5 \sqrt{x})}^{2} + \log_{2} 16 x = 12 \\ \log_{2} (25 x) + \log_{2} 16 x = 12 \\ \log_{2} (25 x) (16 x) = 12 \\ \log_{2} 400 x^{2} = 12 \\ 400 x^{2} = 2^{12} \\ x^{2} = 10.24 \\ x = 3.2 \end{array}$

Question 13

Given that 2 log₂ (x – y) = 3 + log₂x + log₂ y.

Prove that x² + y²– 10xy = 0.

Solution:

2 log₂ (x – y) = 3 + log₂x + log₂ y

log₂ (x– y)² = log₂ 8 + log₂ x + log₂y

log₂ (x– y)² = log₂ 8xy

(x – y)² = 8xy

x²– 2xy + y² = 8xy

x² + y² – 10xy = 0 (proven)

Question 14 (2 marks):
Given 2^p + 2^p = 2^k. Express p in terms of k.

Solution:

$\begin{array}{l} 2^{p} + 2^{p} = 2^{k} \\ 2 (2^{p}) = 2^{k} \\ 2^{p} = \frac{2^{k}}{2^{1}} \\ 2^{p} = 2^{k - 1} \\ p = k - 1 \end{array}$

Short Questions (Question 9 – 11)

Posted on April 21, 2020 by user

Question 9

Solve the equation,

$\log_{2} 4 x = 1 - \log_{4} x$

Solution:

$\begin{array}{l} \log_{2} 4 x = 1 - \log_{4} x \\ \log_{2} 4 x = 1 - \frac{\log_{2} x}{\log_{2} 4} \\ \log_{2} 4 x = 1 - \frac{\log_{2} x}{2} \\ 2 \log_{2} 4 x = 2 - \log_{2} x \\ \log_{2} 16 x^{2} = \log_{2} 4 - \log_{2} x \\ \log_{2} 16 x^{2} = \log_{2} \frac{4}{x} \\ 16 x^{2} = \frac{4}{x} \\ x^{3} = \frac{4}{16} = \frac{1}{4} \\ x = {(\frac{1}{4})}^{\frac{1}{3}} = 0.62996 \end{array}$

Question 10

Solve the equation,

$\log_{4} x = 25 \log_{x} 4$

Solution:

$\begin{array}{l} \log_{4} x = 25 \log_{x} 4 \\ \frac{1}{\log_{x} 4} = 25 \log_{x} 4 \\ \frac{1}{25} = {(\log_{x} 4)}^{2} \\ \log_{x} 4 = \pm \frac{1}{5} \\ \log_{x} 4 = \frac{1}{5} or \log_{x} 4 = - \frac{1}{5} \\ 4 = x^{\frac{1}{5}} 4 = x^{- \frac{1}{5}} \\ x = 4^{5} 4 = \frac{1}{x^{\frac{1}{5}}} \\ x = 1024 x^{\frac{1}{5}} = \frac{1}{4} \\ x = \frac{1}{1024} \end{array}$

Question 11

Solve the equation,

$2 \log_{x} 5 + \log_{5} x = \lg 1000$

Solution:

$\begin{array}{l} 2 \log_{x} 5 + \log_{5} x = \lg 1000 \\ 2. \frac{1}{\log_{5} x} + \log_{5} x = 3 \\ \times (\log_{5} x) \to 2 + {(\log_{5} x)}^{2} = 3 \log_{5} x \\ {(\log_{5} x)}^{2} - 3 \log_{5} x + 2 = 0 \\ (\log_{5} x - 2) (\log_{5} x - 1) = 0 \\ \log_{5} x = 2 or \log_{5} x = 1 \\ x = 5^{2} x = 5 \\ x = 25 \end{array}$

Short Questions (Question 5 – 8)

Posted on April 21, 2020 by user

Question 5

Solve the equation,

$\log_{9} (x - 2) = \log_{3} 2$

Solution:

$\begin{array}{l} \log_{9} (x - 2) = \log_{3} 2 \\ \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \Rightarrow \frac{\log_{3} (x - 2)}{\log_{3} 9} = \log_{3} 2 \\ \frac{\log_{3} (x - 2)}{2} = \log_{3} 2 \\ \log_{3} (x - 2) = 2 \log_{3} 2 \\ \log_{3} (x - 2) = \log_{3} 2^{2} \\ x - 2 = 4 \\ x = 6 \end{array}$

Question 6

Solve the equation,

$\log_{9} (2 x + 12) = \log_{3} (x + 2)$

Solution:

$\begin{array}{l} \log_{9} (2 x + 12) = \log_{3} (x + 2) \\ \frac{\log_{3} (2 x + 12)}{\log_{3} 9} = \log_{3} (x + 2) \\ \log_{3} (2 x + 12) = 2 \log_{3} (x + 2) \\ \log_{3} (2 x + 12) = \log_{3} {(x + 2)}^{2} \\ 2 x + 12 = x^{2} + 4 x + 4 \\ x^{2} + 2 x - 8 = 0 \\ (x + 4) (x - 2) = 0 \\ x = - 4 (not accepted) \\ x = 2 \end{array}$

Question 7

Solve the equation,

$\log_{4} x = \frac{3}{2} \log_{2} 3$

Solution:

$\begin{array}{l} \log_{4} x = \frac{3}{2} \log_{2} 3 \\ \frac{\log_{2} x}{\log_{2} 4} = \frac{3}{2} \log_{2} 3 \\ \frac{\log_{2} x}{2} = \frac{3}{2} \log_{2} 3 \\ \log_{2} x = 2 \times \frac{3}{2} \log_{2} 3 \\ \log_{2} x = 3 \log_{2} 3 \\ \log_{2} x = \log_{2} 3^{3} \\ x = 27 \end{array}$

Question 8

Solve the equation,

$\frac{2}{\log_{5} 2} = \log_{2} (2 - x)$

Solution:

$\begin{array}{l} \frac{2}{\log_{5} 2} = \log_{2} (2 - x) \\ 2 = \log_{5} 2. \log_{2} (2 - x) \\ 2 = \frac{1}{\log_{2} 5} . \log_{2} (2 - x) \\ 2 \log_{2} 5 = \log_{2} (2 - x) \\ \log_{2} 5^{2} = \log_{2} (2 - x) \\ 25 = 2 - x \\ x = - 23 \end{array}$

Short Questions (Question 1 – 4)

Posted on April 21, 2020 by user

Question 1

Solve the equation, log₃ [log₂(2x – 1)] = 2

Solution:

log₃ [log₂ (2x – 1)] = 2 ← (if log _aN = x, N = a^x)

log₂ (2x – 1) = 3²
log₂ (2x – 1) = 9

2x – 1 = 2⁹

x = 256.5

Question 2

Solve the equation,

$l o g_{16} [l o g_{2} (5 x - 4)] = l o g_{9} \sqrt{3}$

Solution:

$\begin{array}{l} l o g_{16} [l o g_{2} (5 x - 4)] = l o g_{9} \sqrt{3} \\ l o g_{16} [l o g_{2} (5 x - 4)] = \frac{1}{4} \leftarrow \begin{array}{l} \log_{9} \sqrt{3} = \log_{9} 3^{\frac{1}{2}} = \frac{1}{2} \log_{9} 3 \\ = \frac{1}{2} (\frac{1}{\log_{3} 9}) = \frac{1}{2} (\frac{1}{2}) = \frac{1}{4} \end{array} \\ l o g_{2} (5 x - 4) = 16^{\frac{1}{4}} \\ l o g_{2} (5 x - 4) = 2 \\ 5 x - 4 = 2^{2} \\ 5 x = 8 \\ x = \frac{8}{5} \end{array}$

Question 3

Solve the equation,

$5^{\log_{4} x} = 125$

Solution:

$\begin{array}{l} 5^{\log_{4} x} = 125 \\ \log_{5} 5^{\log_{4} x} = \log_{5} 125 \leftarrow put log for both side \\ (\log_{4} x) (\log_{5} 5) = 3 \\ (\log_{4} x) (1) = 3 \\ x = 4^{3} = 64 \end{array}$

Question 4

Solve the equation,

$5^{\log_{5} (x + 1)} = 9$

Solution:

$\begin{array}{l} 5^{\log_{5} (x + 1)} = 9 \\ \log_{5} 5^{^{\log_{5} (x + 1)}} = \log_{5} 9 \\ \log_{5} (x + 1) . \log_{5} 5 = \log_{5} 9 \\ \log_{5} (x + 1) = \log_{5} 9 \\ x + 1 = 9 \\ x = 8 \end{array}$

5.4 Equations Involving Logarithms (Example 4 & 5)

Posted on April 21, 2020 by user

Example 4
Solve the following equation :
(a)

$\log_{9} (x - 2) = \log_{3} 2$
(b)

$\log_{4} x = \frac{3}{2} \log_{2} 3$

Example 5
Solve the following :
(a)

$\log_{4} x = 25 \log_{x} 4$
(b)

$\log_{2} 5 \sqrt{x} + \log_{4} 16 x = 6$