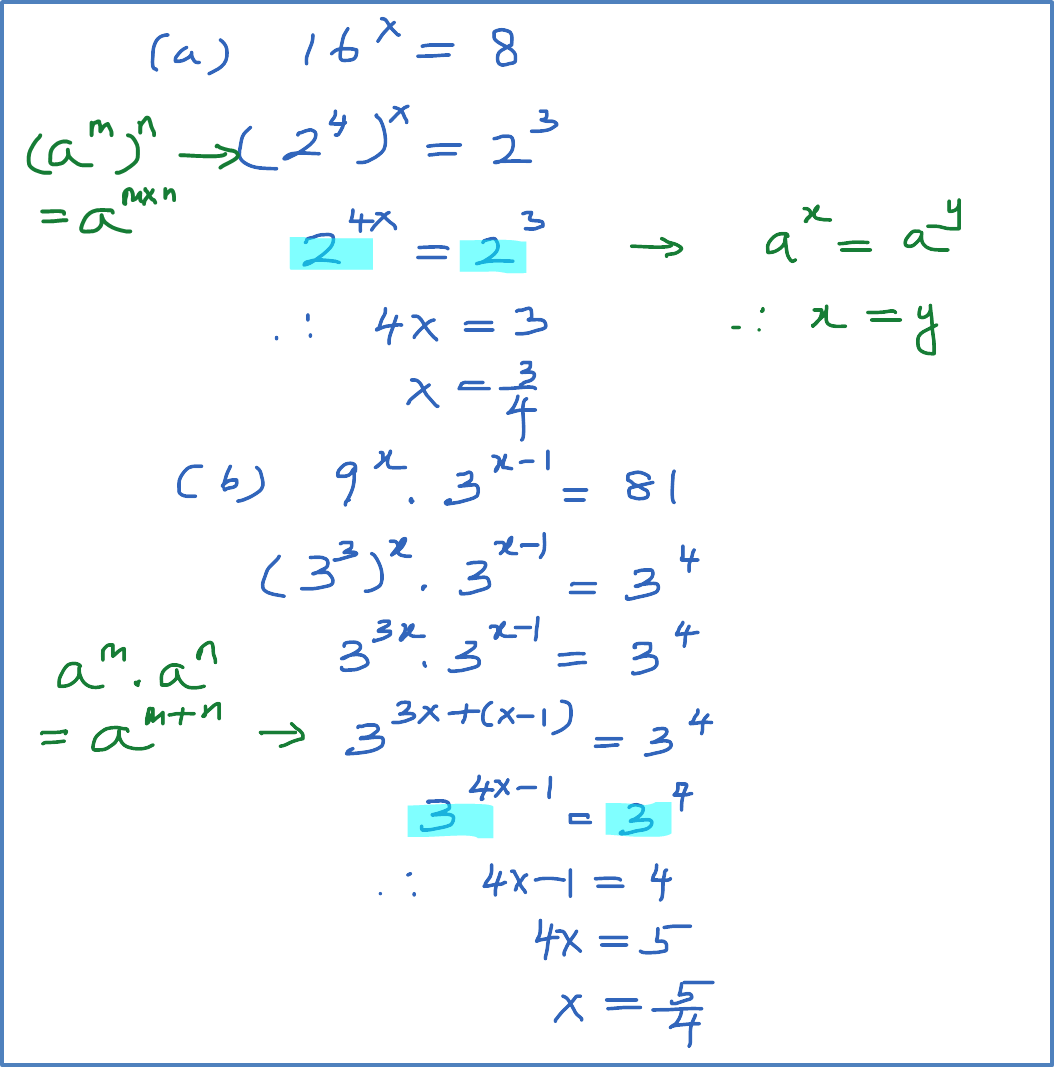
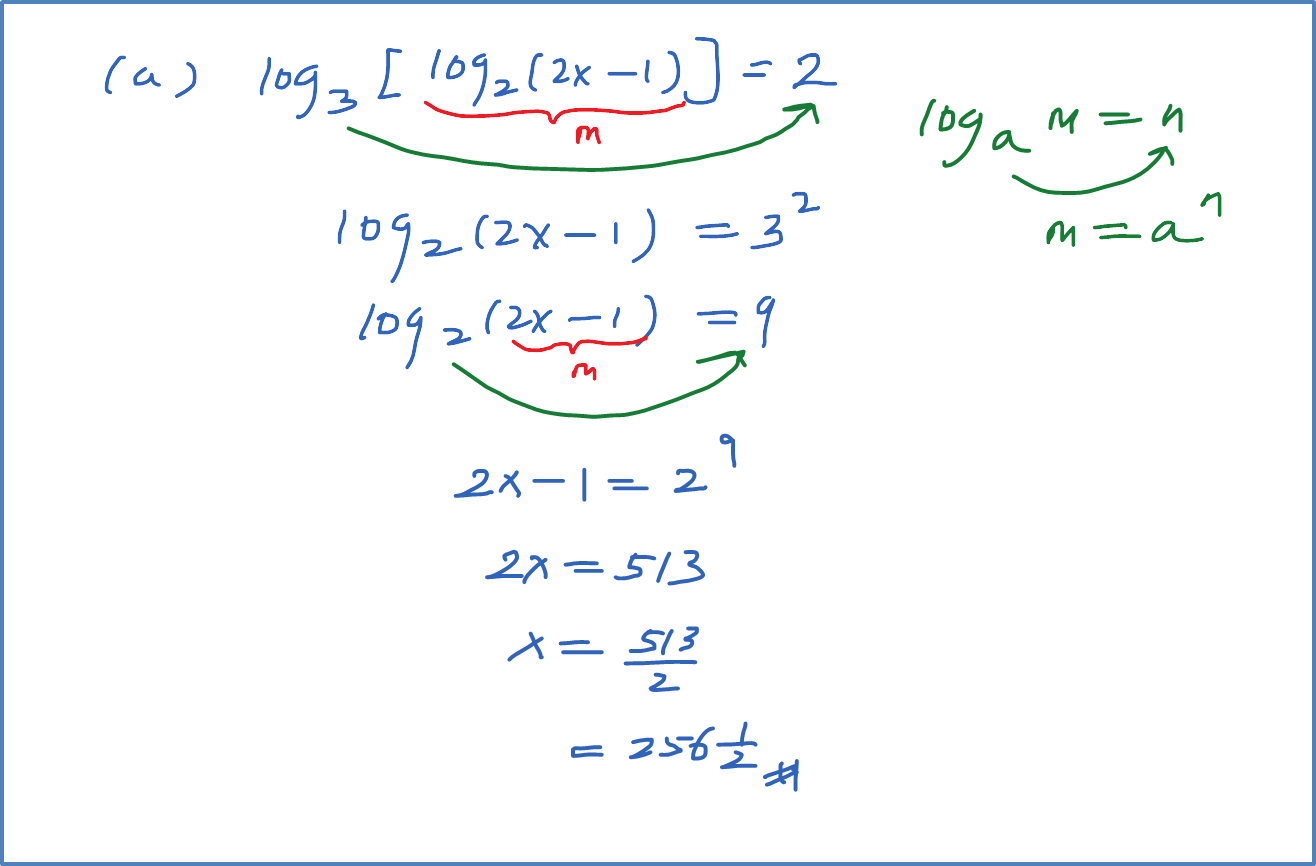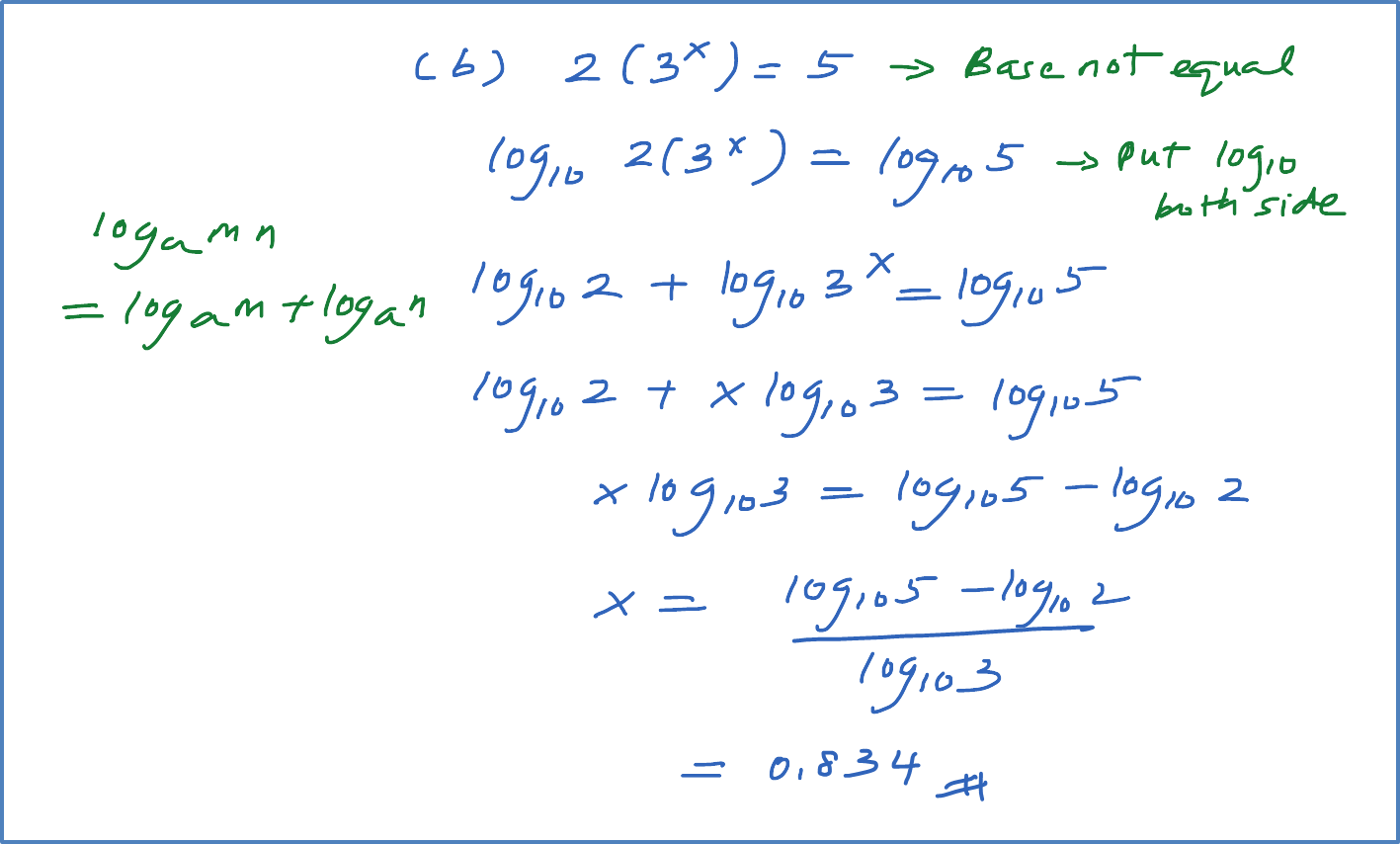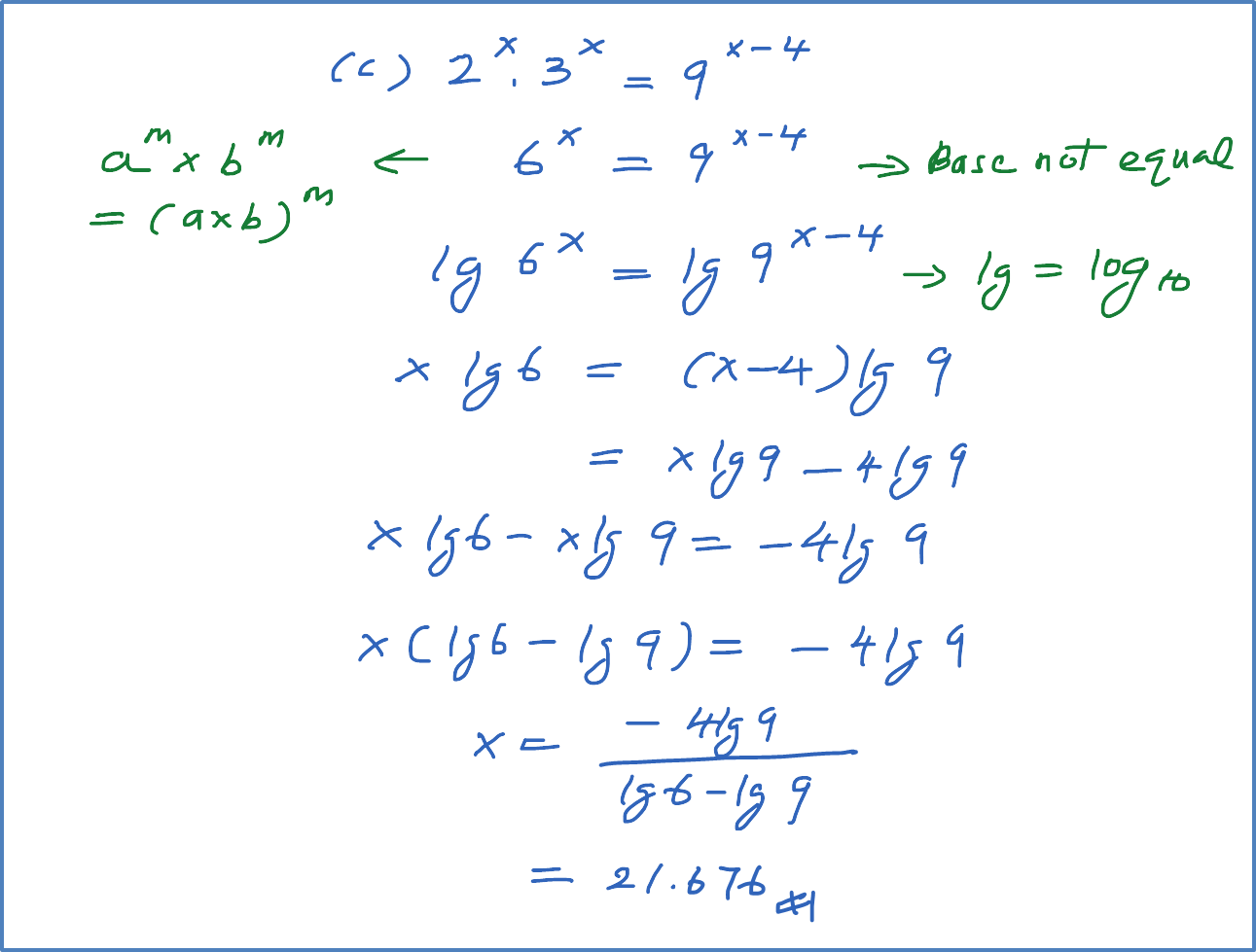Example 2
Solve the following equation:
(a) log√y81−3=log√y3
(b) 2log2x−log2(x2−1)−4=0
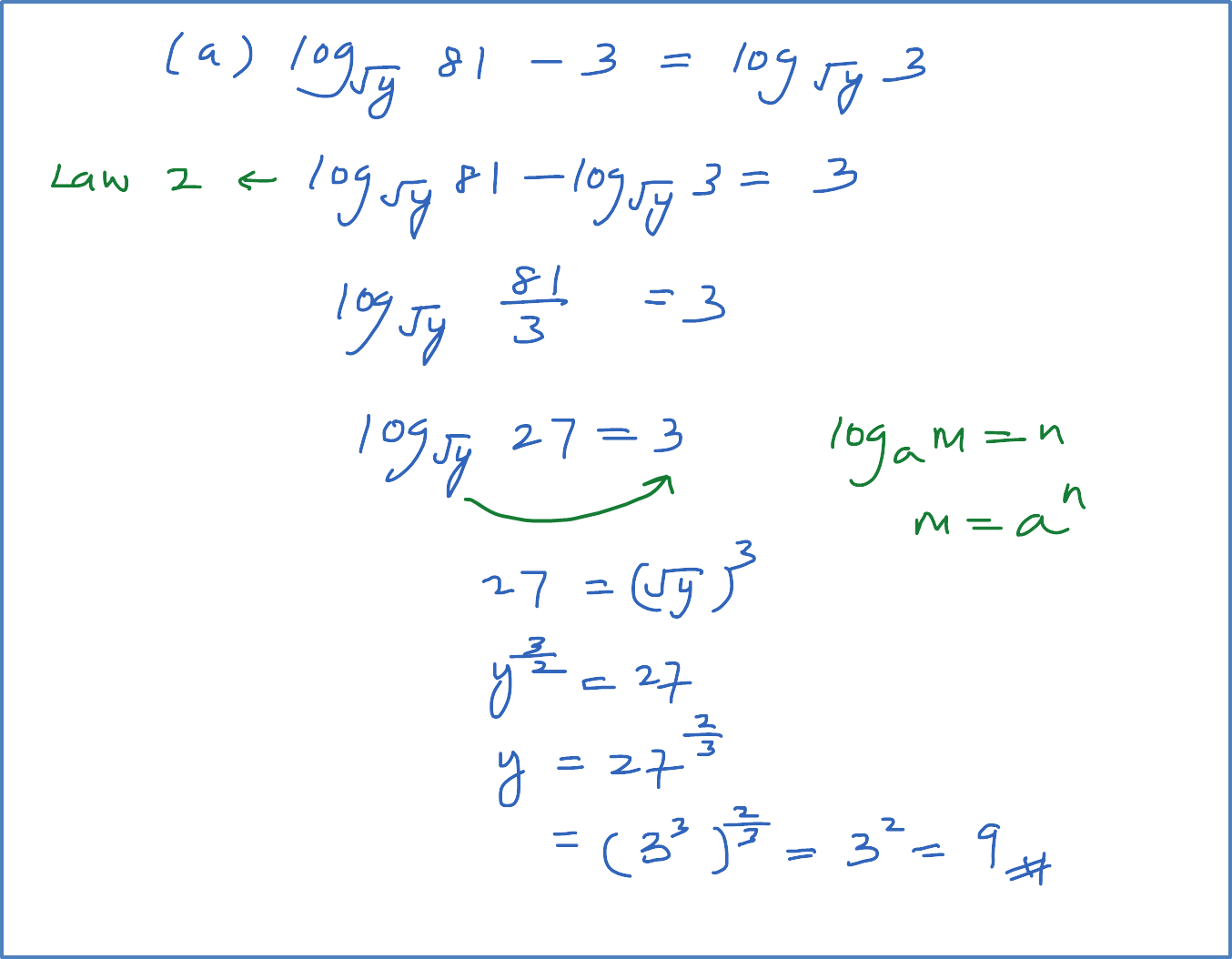

Solve the following equation:
(a) log√y81−3=log√y3
(b) 2log2x−log2(x2−1)−4=0
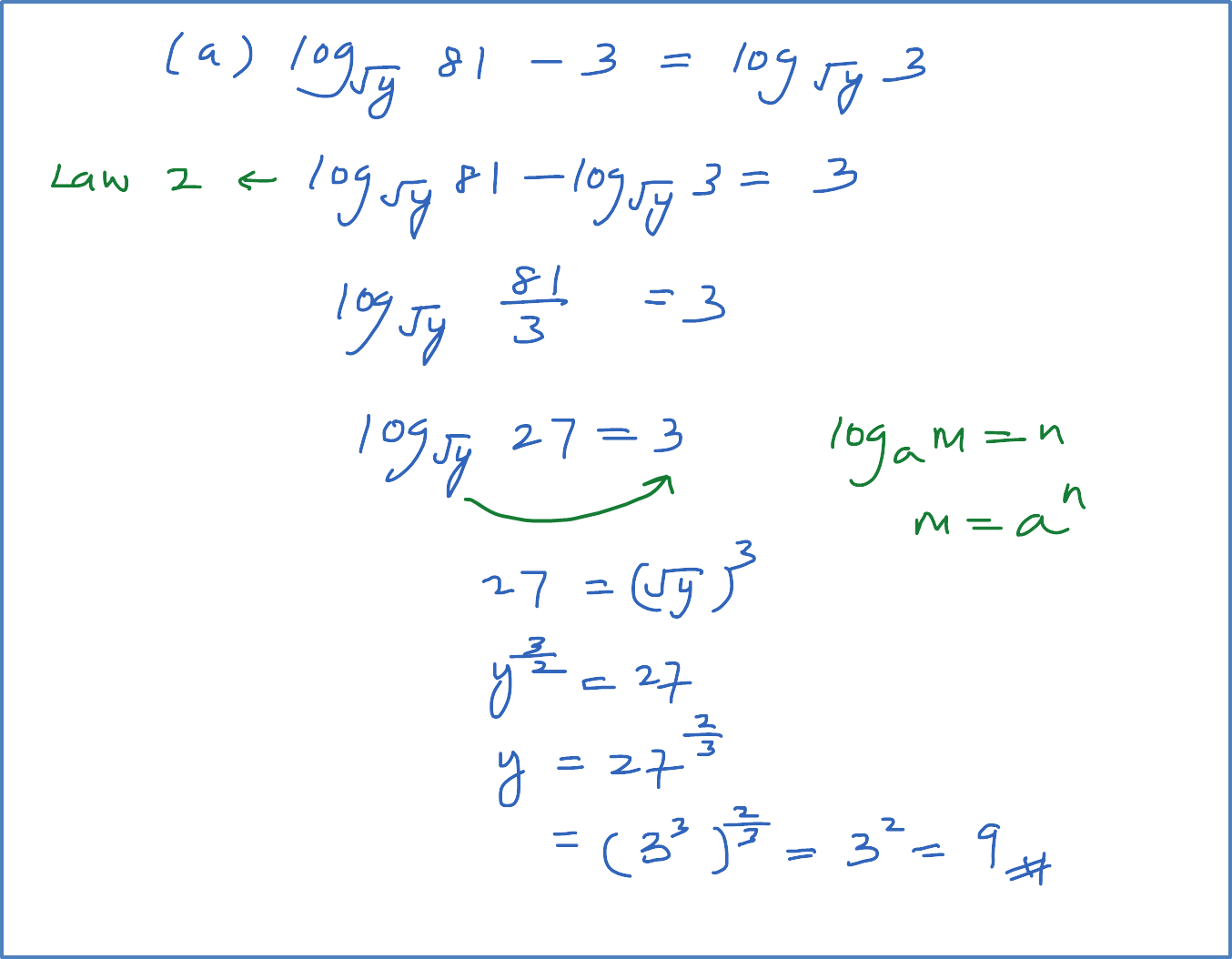

Example 3
Sole the following equation:
(a) log3[log2(2x−1)]=2
(b) log16[log2(5x−4)]=log9√3
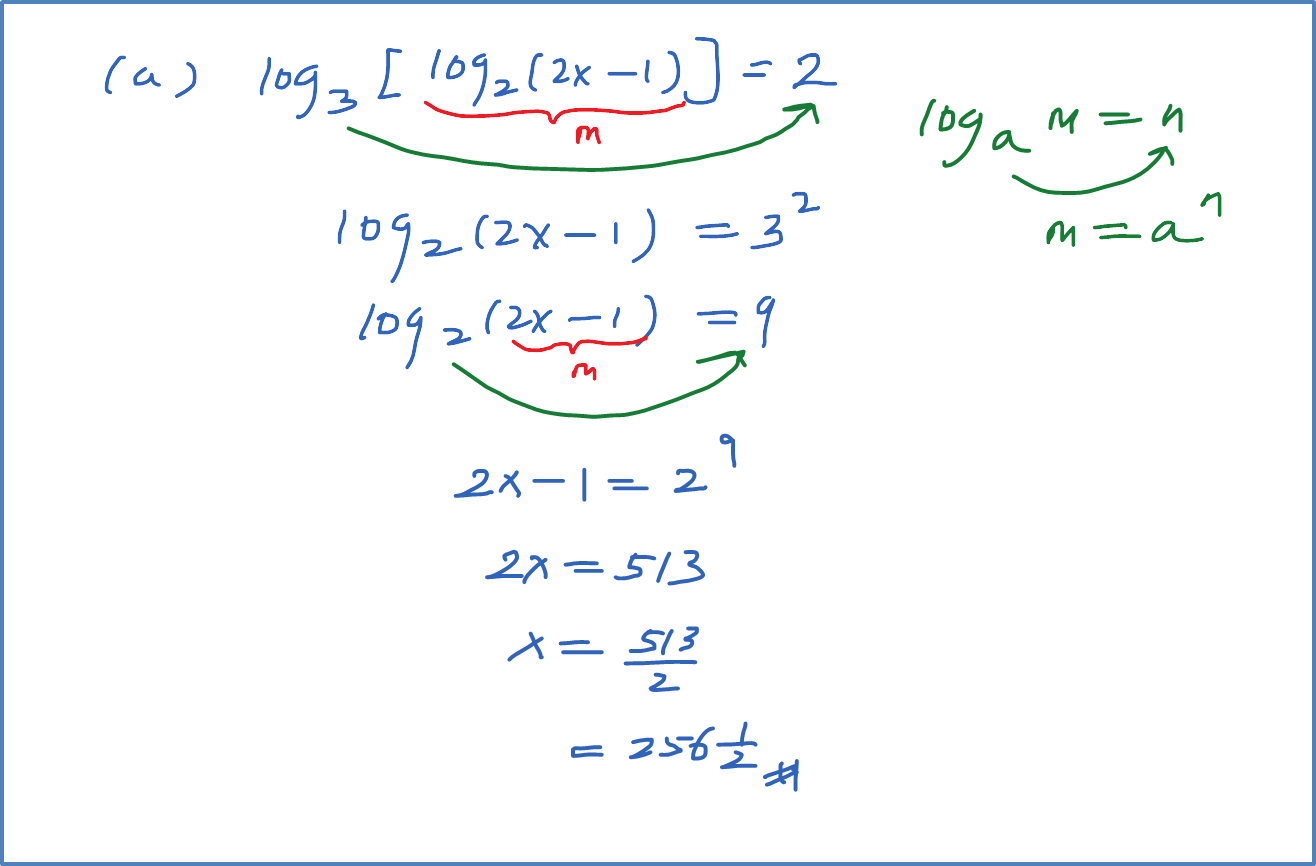

Sole the following equation:
(a) log3[log2(2x−1)]=2
(b) log16[log2(5x−4)]=log9√3