Example 1:
Solution:
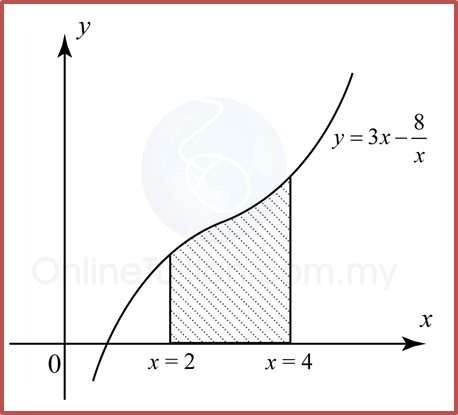
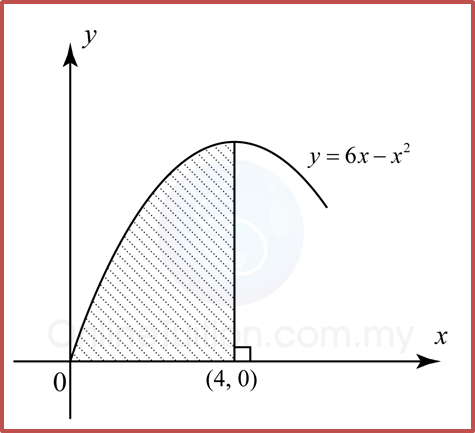
Volume generated, Vx
Vx=π∫bay2dxVx=π∫42(3x−8x)2dxVx=π∫42(3x−8x)(3x−8x)dxVx=π∫42(9x2−48+64x2)dxVx=π[9x33−48x+64x−1−1]42Vx=π[3x3−48x−64x]42Vx=π[(3(4)3−48(4)−644)−(3(2)3−48(2)−642)]Vx=π(−16+104)Vx=88πunit3
Example 2:
Solution:
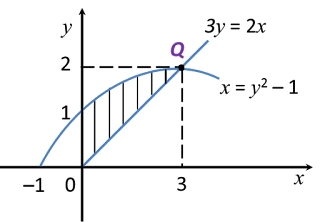
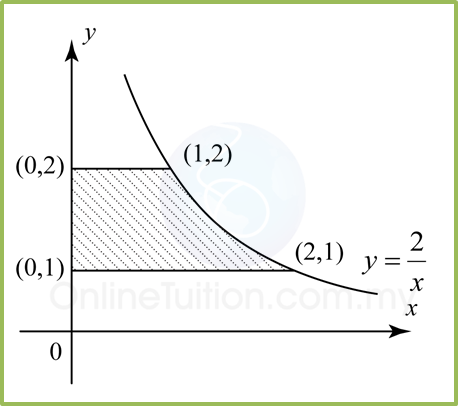
Volume generated, Vy
Vy=π∫bax2dyVy=π∫21(2y)2dyVy=π∫21(4y2)dyVy=π∫214y−2dyVy=π[4y−1−1]21=π[−4y]21Vy=π[(−42)−(−41)]Vy=2πunit3
Find the volume generated for the following diagram when the shaded region is revolved through 360° about the x-axis.
Solution:
Volume generated, Vx
Example 2:
Find the volume generated for the following diagram when the shaded region is revolved through 360° about the y-axis.
Volume generated, Vy


 Diagram
Diagram