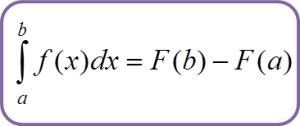3.2 Integration by Substitution

Posted on April 22, 2020 by user

3.2 Integration by Substitution

It is given that

${\int (a x + b)}^{n} d x, n \neq - 1.$

(A) Using the Substitution method,

$\begin{array}{l} Let u = a x + b \\ Thus, \frac{d u}{d x} = a \\ ∴ d x = \frac{d u}{a} \end{array}$

Example 1:

$\begin{array}{l} {\int (3 x + 5)}^{3} d x . \\ Let u = 3 x + 5 \\ \frac{d u}{d x} = 3 \\ d x = \frac{d u}{3} \\ {\int (3 x + 5)}^{3} d x \\ = \int u^{3} \frac{d u}{3} \leftarrow \begin{array}{l} substitute 3 x + 5 = u \\ and d x = \frac{d u}{3} \end{array} \\ = \frac{1}{3} \int u^{3} d u \\ = \frac{1}{3} (\frac{u^{4}}{4}) + c \\ = \frac{1}{3} (\frac{{(3 x + 5)}^{4}}{4}) + c \leftarrow \begin{array}{l} substitute back \\ u = 3 x + 5 \end{array} \\ = \frac{{(3 x + 5)}^{4}}{12} + c \end{array}$

(B) Using Formula method

$\begin{array}{l} \int {(a x + b)}^{n} = \frac{{(a x + b)}^{n + 1}}{(n + 1) a} + c \\ Hence, \\ \int {(3 x + 5)}^{3} d x = \frac{{(3 x + 5)}^{4}}{4 (3)} + c \\ = \frac{{(3 x + 5)}^{4}}{12} + c \end{array}$

Example 2 (Formula method):

Basic Integration

Posted on April 22, 2020 by user

3.1 Integration as the Inverse of Differentiation, Integration of axⁿ and integration of the Functions of the Sum/Difference of Algebraic Terms

Type 1:

$\begin{array}{l} \int a d x = a x + C \\ Example \\ \int 2 d x = 2 x + C \end{array}$

Type 2:

$\begin{array}{l} \int a x^{n} d x = \frac{a x^{n + 1}}{n + 1} + C \\ E x a m p l e 1 \\ \int 2 x^{3} d x = \frac{2 x^{4}}{4} + C = \frac{x^{4}}{2} + C \\ E x a m p l e 2 \\ \int \frac{2}{3 x^{5}} d x = \int \frac{2}{3} x^{- 5} d x = \frac{2}{3} (\frac{x^{- 4}}{- 4}) + C \\ = \frac{2}{3} (\frac{x^{- 4}}{- 4}) + C = \frac{x^{- 4}}{- 6} + C \end{array}$

Type 3:

$\begin{array}{l} \int (u + v) d x = \int u d x \pm \int v d x \\ u and v are functions in x \\ E x a m p l e 1 \\ \int 3 x^{2} + 2 x d x = \int 3 x^{2} d x + \int 2 x d x \\ = \frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} + C \\ = \frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} + C \\ = x^{3} + x^{2} + C \end{array}$

$\begin{array}{l} E x a m p l e 2 \\ \int (x + 2) (3 x + 1) d x = \int 3 x^{2} + 7 x + 2 d x \\ = \int 3 x^{2} d x + \int 7 x d x + \int 2 d x \\ = \frac{3 x^{3}}{3} + \frac{7 x^{2}}{2} + 2 x + C \\ = x^{3} + \frac{7 x^{2}}{2} + 2 x + C \end{array}$

$\begin{array}{l} E x a m p l e 3 \\ \int \frac{3 x^{3} + x^{2} - x}{x} d x = \int 3 x^{2} + x - 1 d x \\ = \int 3 x^{2} d x + \int x d x - \int 1 d x \\ = \frac{3 x^{3}}{3} + \frac{x^{2}}{2} - x + C \\ = x^{3} + \frac{x^{2}}{2} - x + C \end{array}$

Finding Equation Of A Curve From Its Gradient Function

Posted on April 22, 2020 by user

3.3 Finding Equation of a Curve from its Gradient Function

Example 1:
Find the equation of the curve that has the gradient function

$\frac{d y}{d x} = 2 x + 8$ and passes through the point (2, 3).

Solution:

$\begin{array}{l} y = \int (2 x + 8) \\ y = \frac{2 x^{2}}{2} + 8 x + C \end{array}$

y = x² + 8x + C

3 = 2² +8(2) + C (2, 3)

C = –17
Hence, the equation of the curve is
y = x² + 8x – 17

Example 2:

The gradient function of a curve is given by 2x – 4 and the curve has a minimum value of 3. Find the equation of the curve.

Solution:

At the point where a curve has a minimum value,

$\frac{d y}{d x} = 0$

2x – 4 = 0

x = 2

Therefore minimum point = (2, 3).

$\begin{array}{l} \frac{d y}{d x} = 2 x - 4 \\ y = \int (2 x - 4) d x \\ y = \frac{2 x^{2}}{2} - 4 x + C \\ y = x^{2} - 4 x + C \end{array}$

When x = 2, y = 3.

3 = 2² – 4(2) + c

c = 7

Hence, the equation of the curve is

y = x² – 4x + 7

Definite Integrals

Posted on April 22, 2020 by user

3.4a Definite Integral of f(x) from x=a to x=b

Example:

Evaluate each of the following.

$\begin{array}{l} (a) \int_{- 1}^{0} (3 x^{2} - 2 x + 5) d x \\ (b) \int_{0}^{2} {(2 x + 1)}^{3} d x \end{array}$

Solution:

$\begin{array}{l} (a) \int_{- 1}^{0} (3 x^{2} - 2 x + 5) d x \\ = {[\frac{3 x^{3}}{3} - \frac{2 x^{2}}{2} + 5 x]}_{- 1}^{0} \\ = {[x^{3} - x^{2} + 5 x]}_{- 1}^{0} \\ = 0 - [{(- 1)}^{3} - {(- 1)}^{2} + 5 (- 1)] \\ = 0 - (- 1 - 1 - 5) \\ = 7 \\ (b) \int_{0}^{2} {(2 x + 1)}^{3} d x \\ = {[\frac{{(2 x + 1)}^{4}}{4 (2)}]}_{0}^{2} \\ = {[\frac{{(2 x + 1)}^{4}}{8}]}_{0}^{2} \\ = [\frac{{(2 (2) + 1)}^{4}}{8}] - [\frac{{(2 (0) + 1)}^{4}}{8}] \\ = \frac{625}{8} - \frac{1}{8} \\ = 78 \end{array}$

Short Question 2 – 4

Posted on April 22, 2020 by user

Question 2:

Given that

$Given that \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c,$

find the values of m and n.

Solution:

$\begin{array}{l} \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c \\ \int 4 {(1 + x)}^{- 4} d x = m {(1 + x)}^{n} + c \\ \frac{4 {(1 + x)}^{- 3}}{- 3 (1)} + c = m {(1 + x)}^{n} + c \\ - \frac{4}{3} {(1 + x)}^{- 3} + c = m {(1 + x)}^{n} + c \\ m = - \frac{4}{3}, n = - 3 \end{array}$

Question 3:

$\begin{array}{l} Given \int_{- 1}^{2} 2 g (x) d x = 4, and \int_{- 1}^{2} [m x + 3 g (x)] d x = 15. \\ Find the value of constant m . \end{array}$

Solution:

$\begin{array}{l} \int_{- 1}^{2} [m x + 3 g (x)] d x = 15 \\ \int_{- 1}^{2} m x d x + \int_{- 1}^{2} 3 g (x) d x = 15 \\ {[\frac{m x^{2}}{2}]}_{- 1}^{2} + 3 \int_{- 1}^{2} g (x) d x = 15 \\ [\frac{m {(2)}^{2}}{2} - \frac{m {(- 1)}^{2}}{2}] + \frac{3}{2} \int_{- 1}^{2} 2 g (x) d x = 15 \\ 2 m - \frac{1}{2} m + \frac{3}{2} (4) = 15 \leftarrow given \int_{- 1}^{2} 2 g (x) d x = 4 \\ \frac{3}{2} m + 6 = 15 \\ \frac{3}{2} m = 9 \\ m = 9 \times \frac{2}{3} \\ m = 6 \end{array}$

Question 4:

$Given \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x), find \int_{1}^{2} g (x) d x .$

Solution:

$\begin{array}{l} Given \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x) \\ \int g (x) d x = \frac{2 x}{3 - x} \\ Thus, \\ \int_{1}^{2} g (x) d x = {[\frac{2 x}{3 - x}]}_{1}^{2} \\ = \frac{2 (2)}{3 - 2} - \frac{2 (1)}{3 - 1} \\ = 4 - 1 \\ = 3 \end{array}$