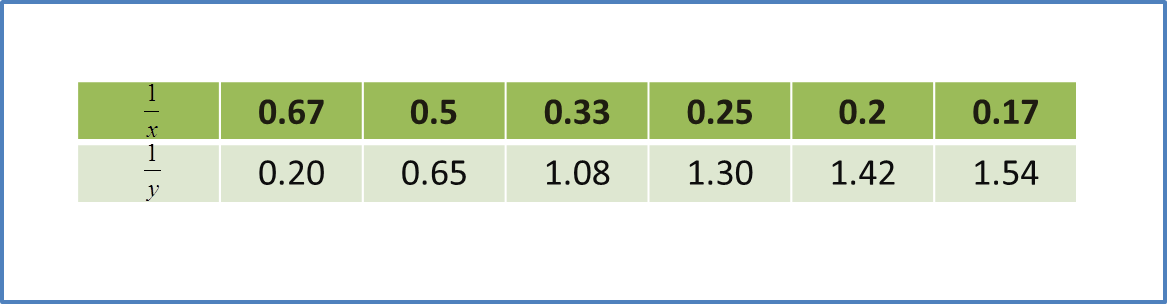
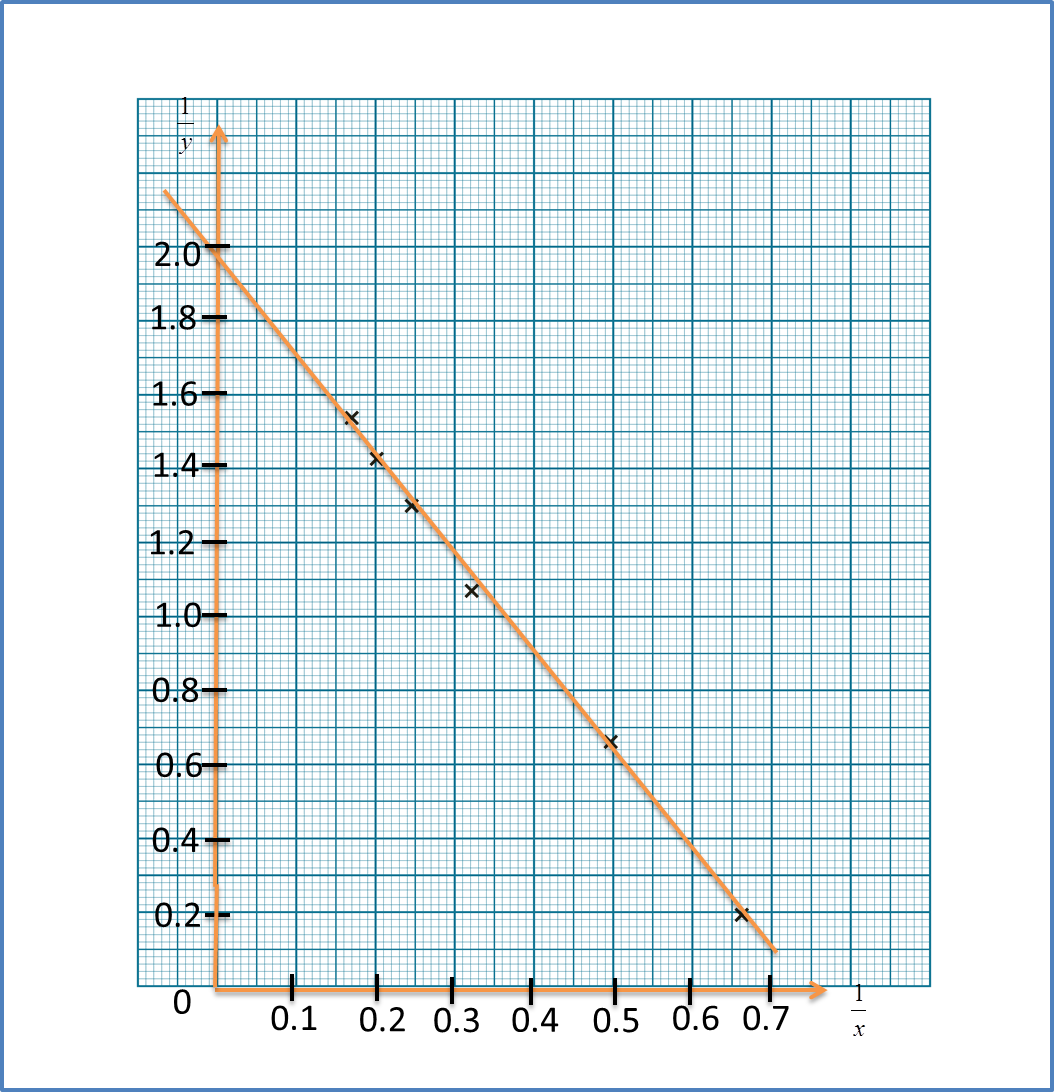
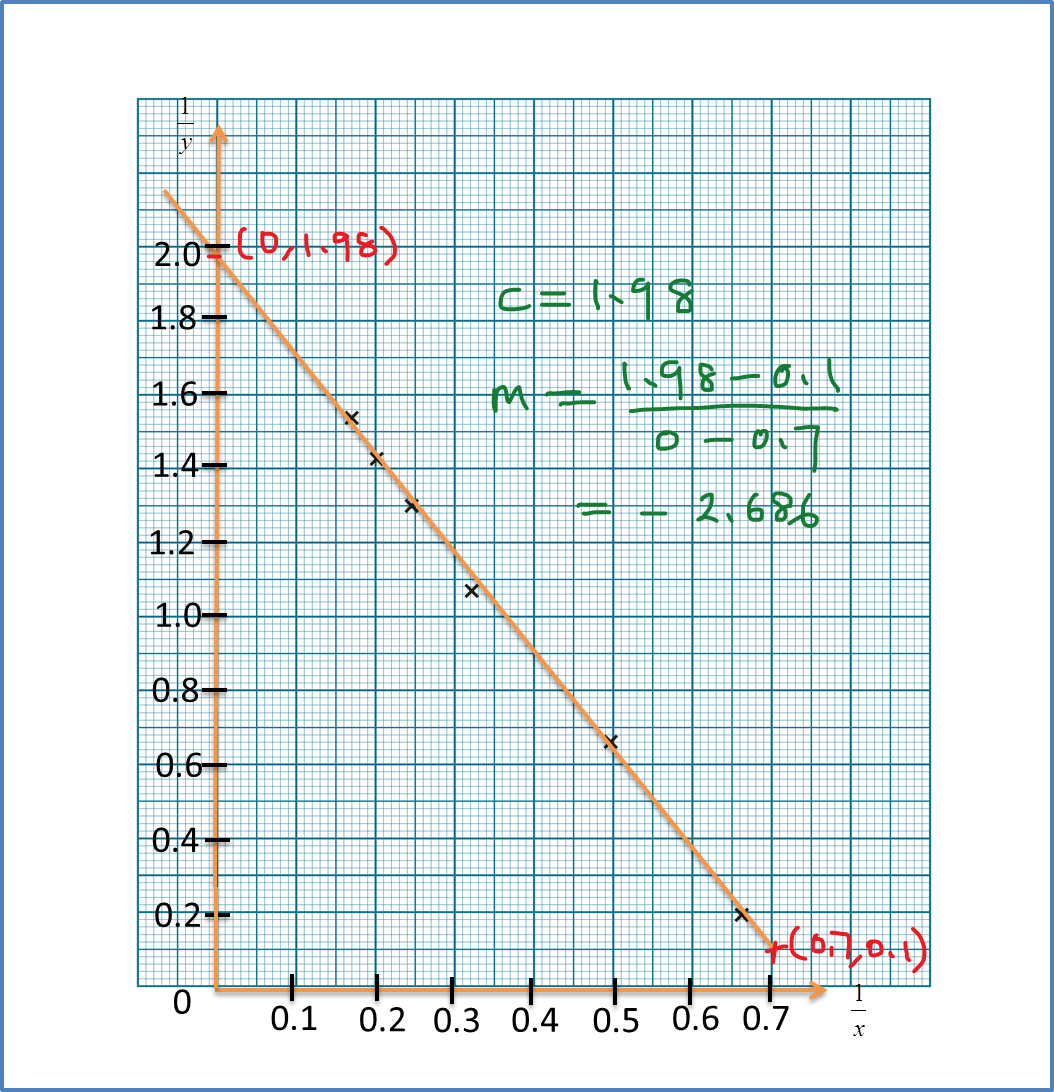
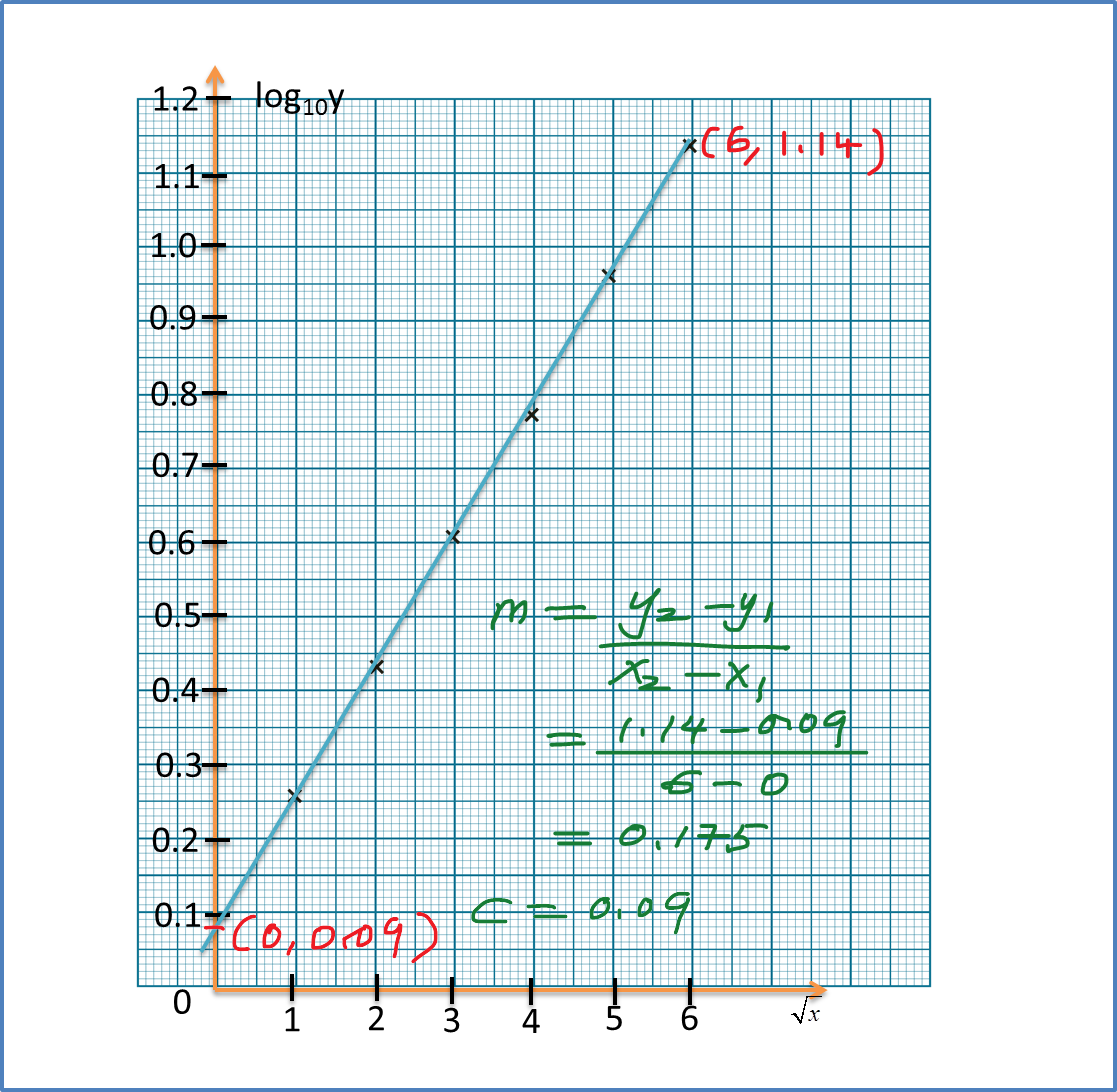
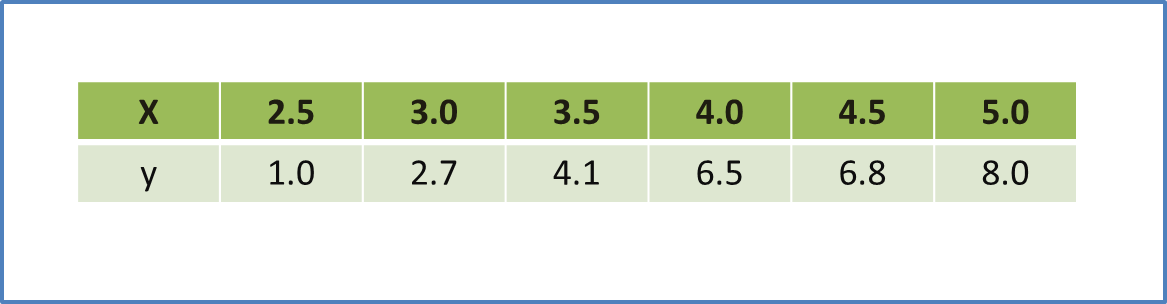
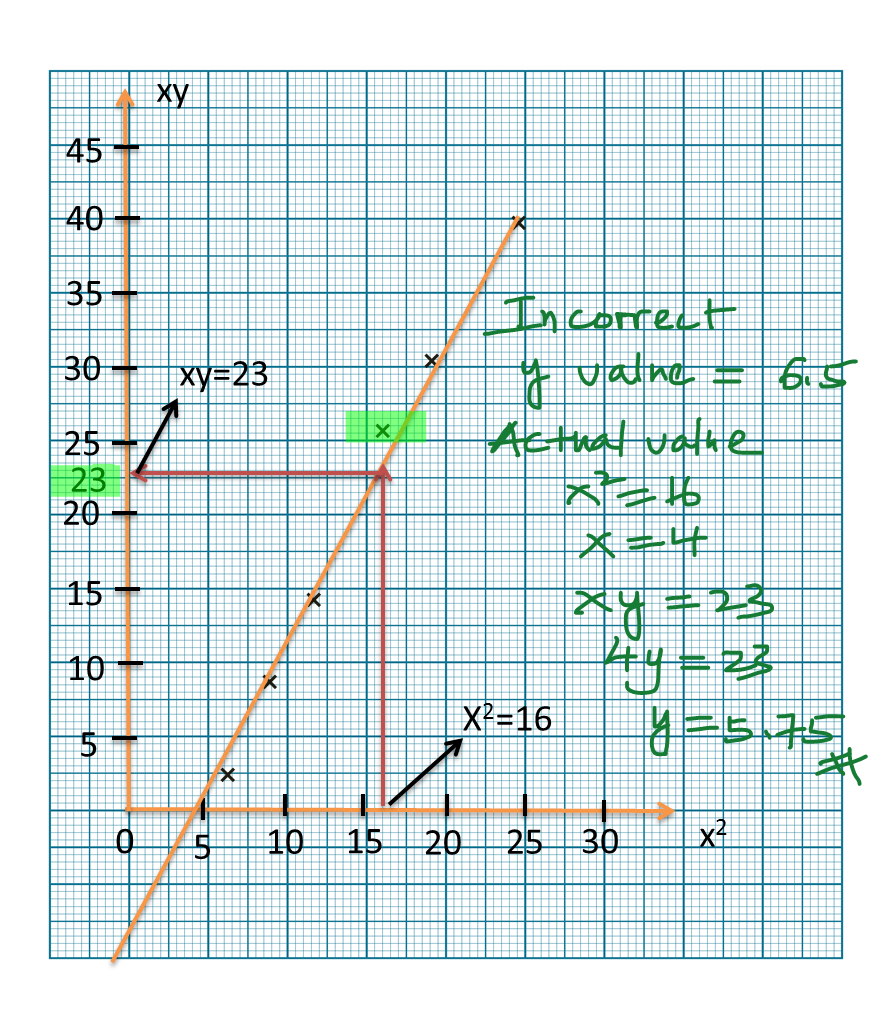
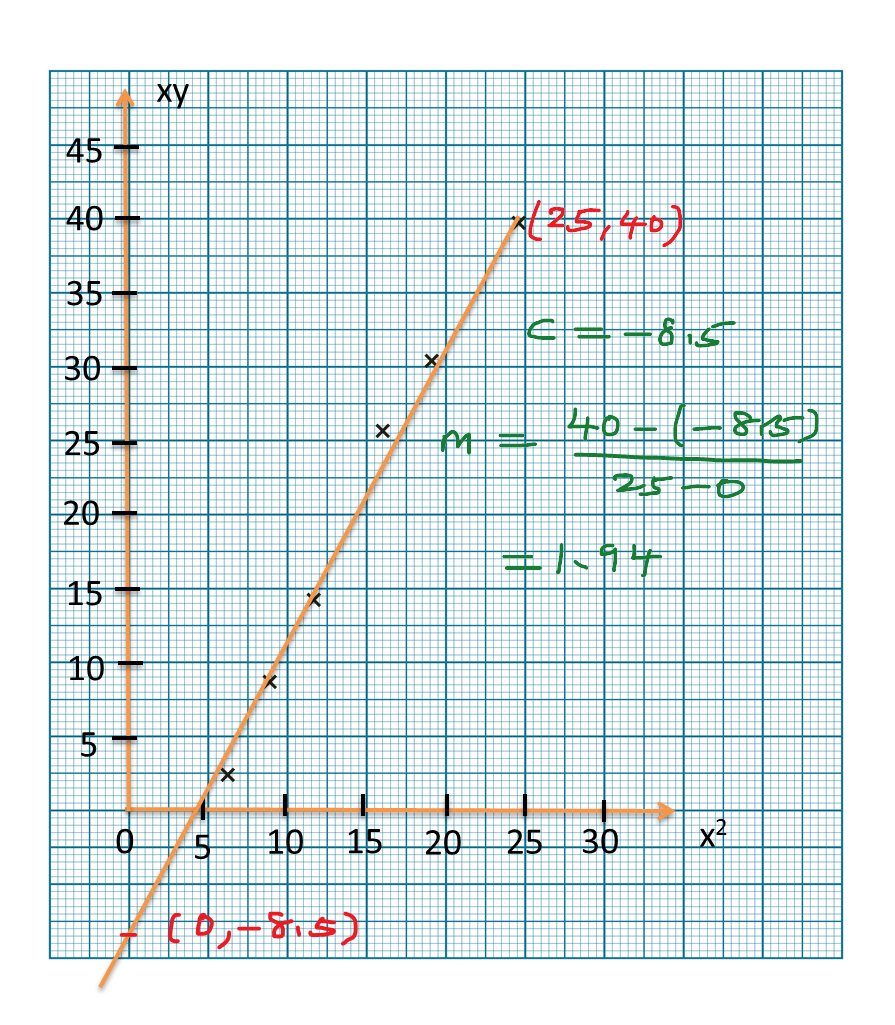
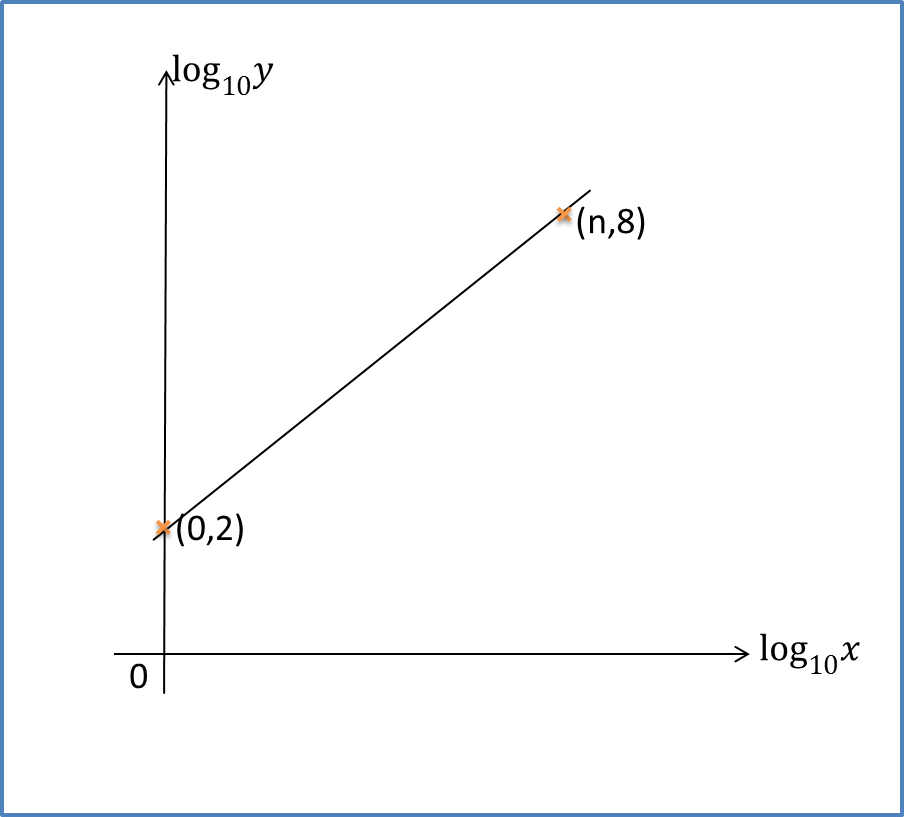
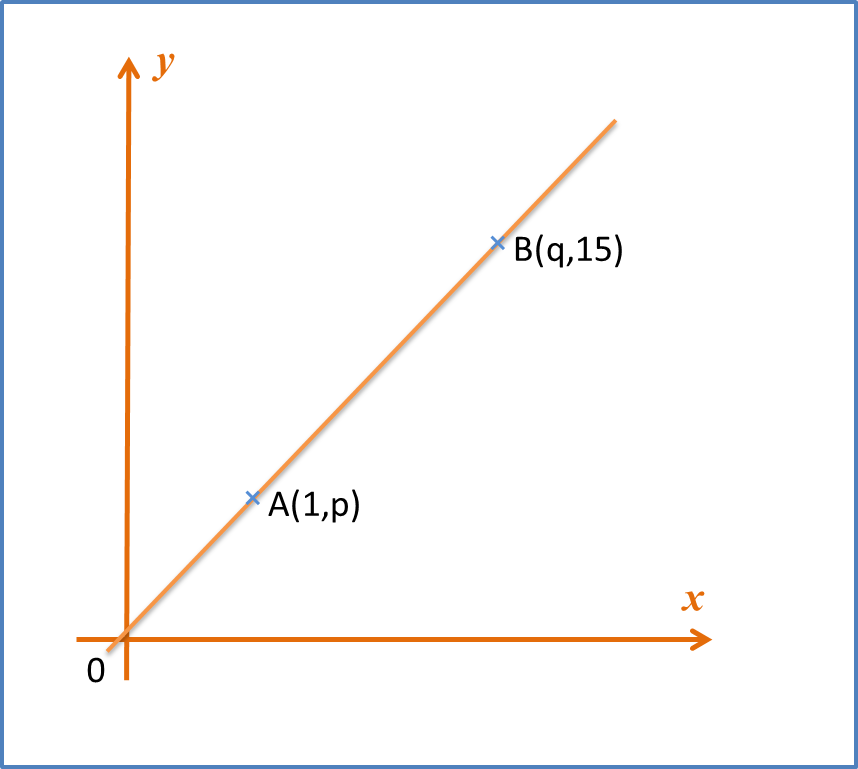
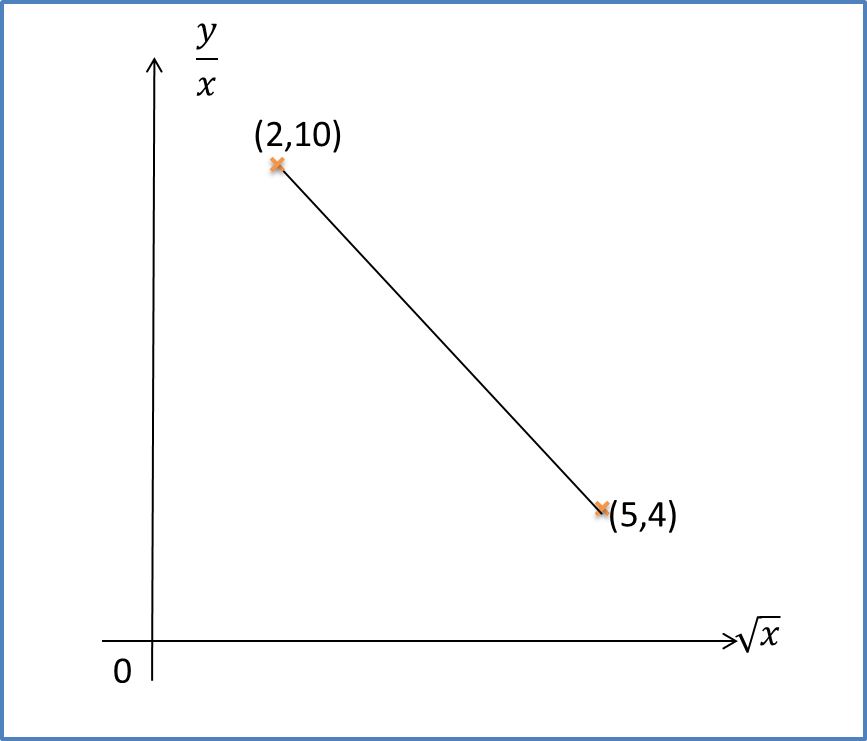
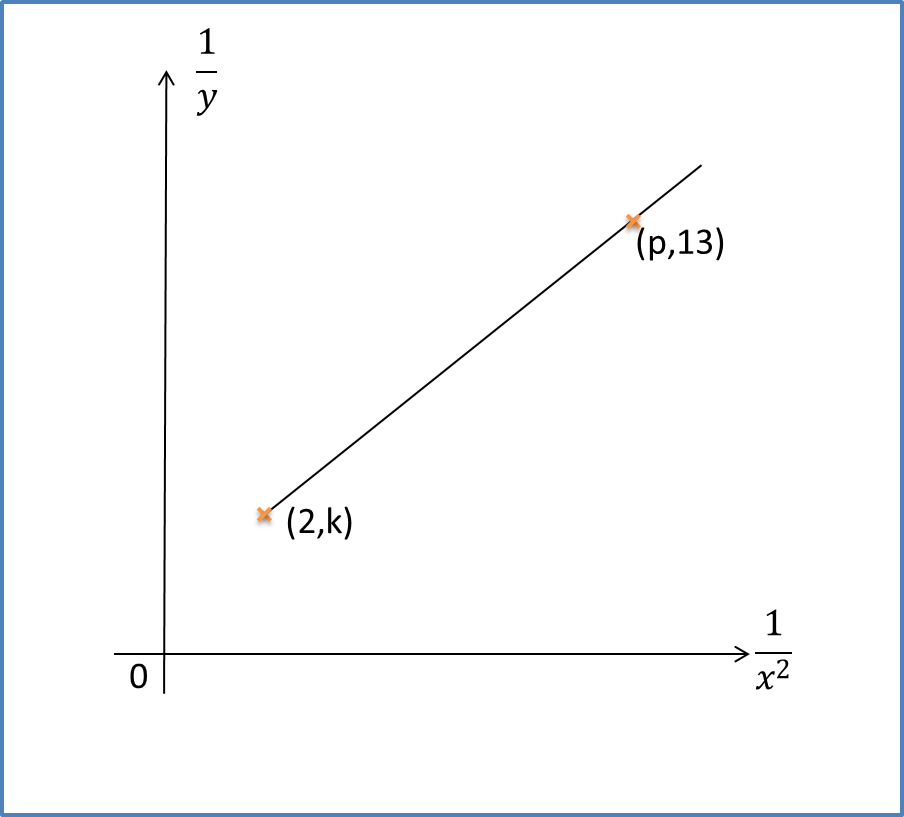
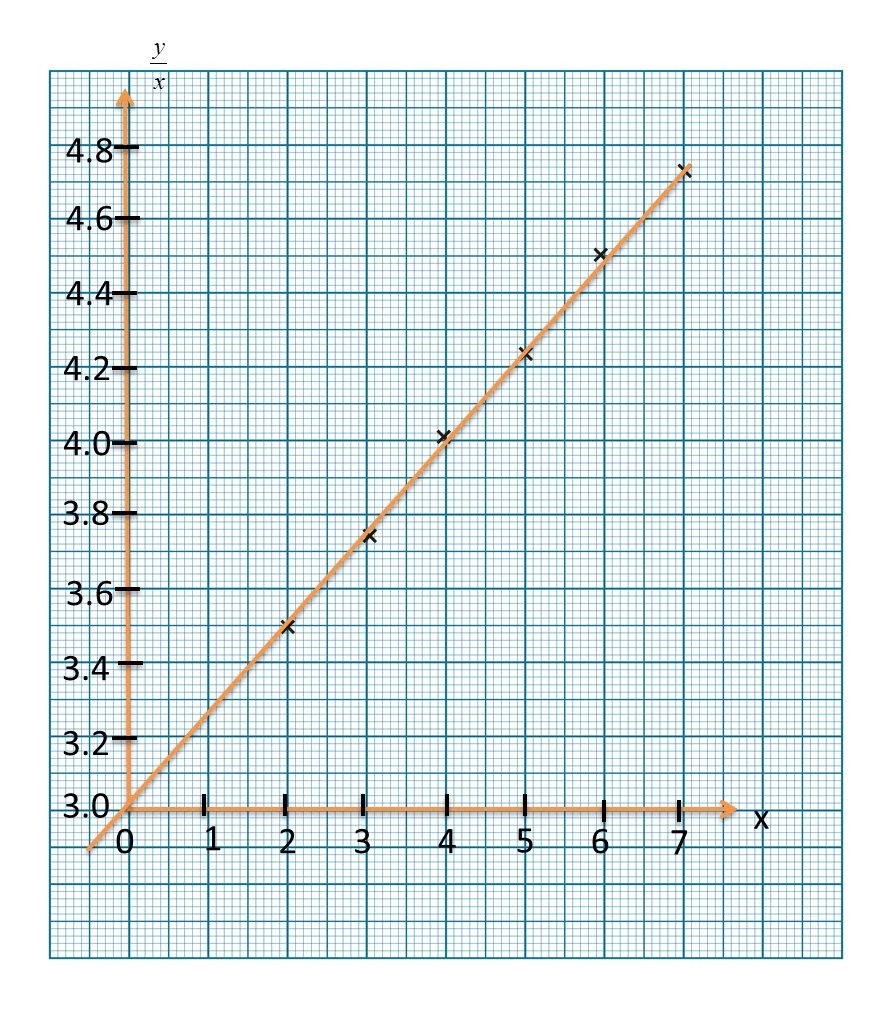
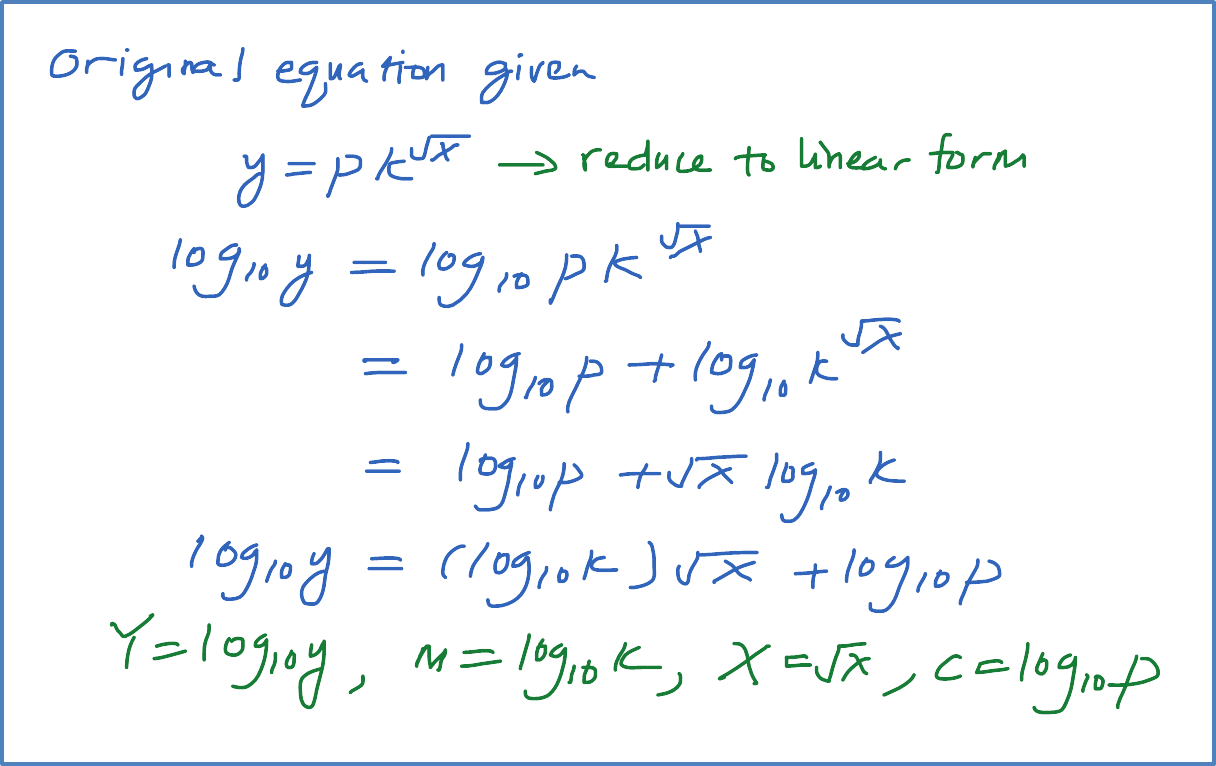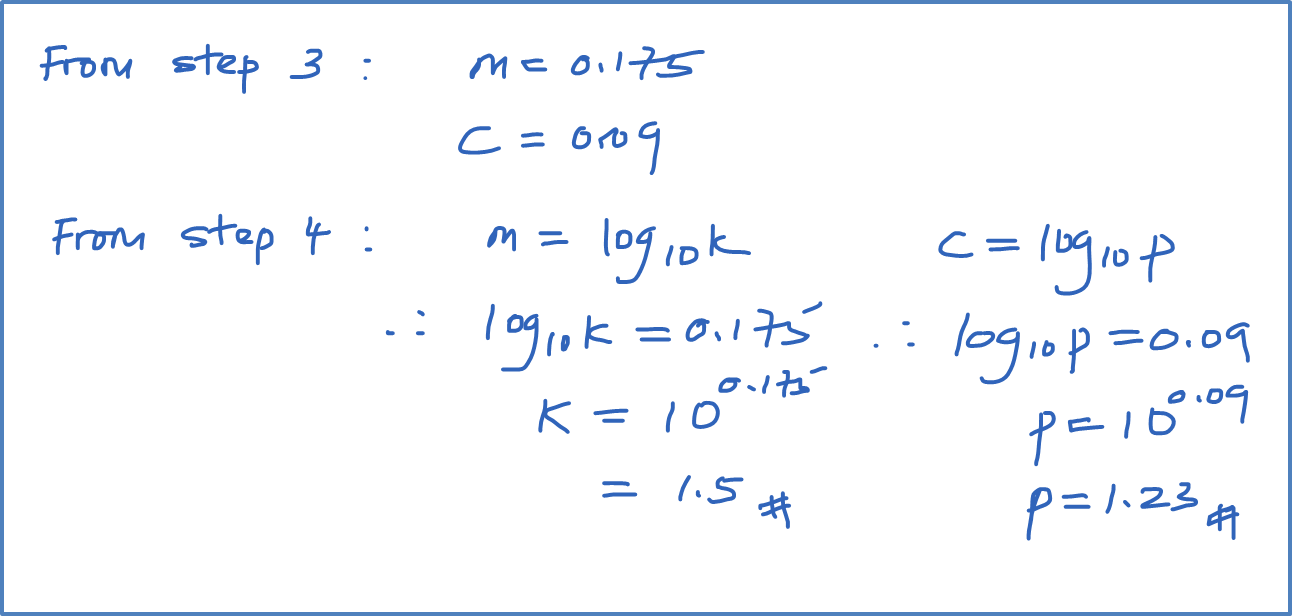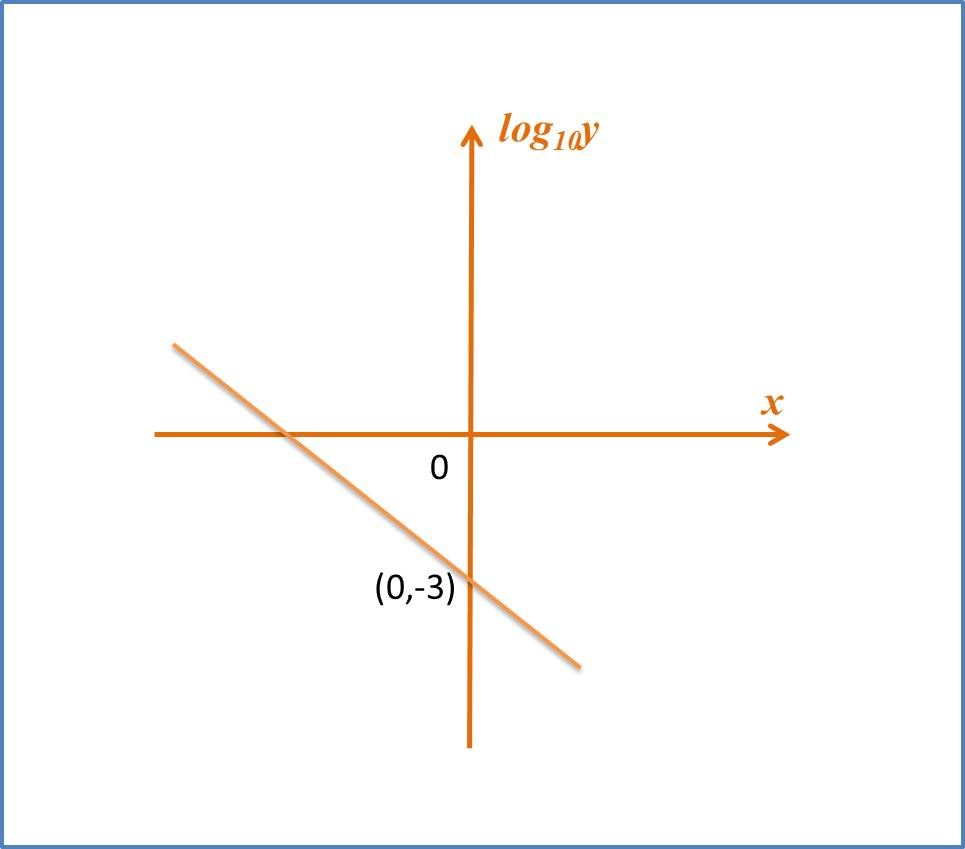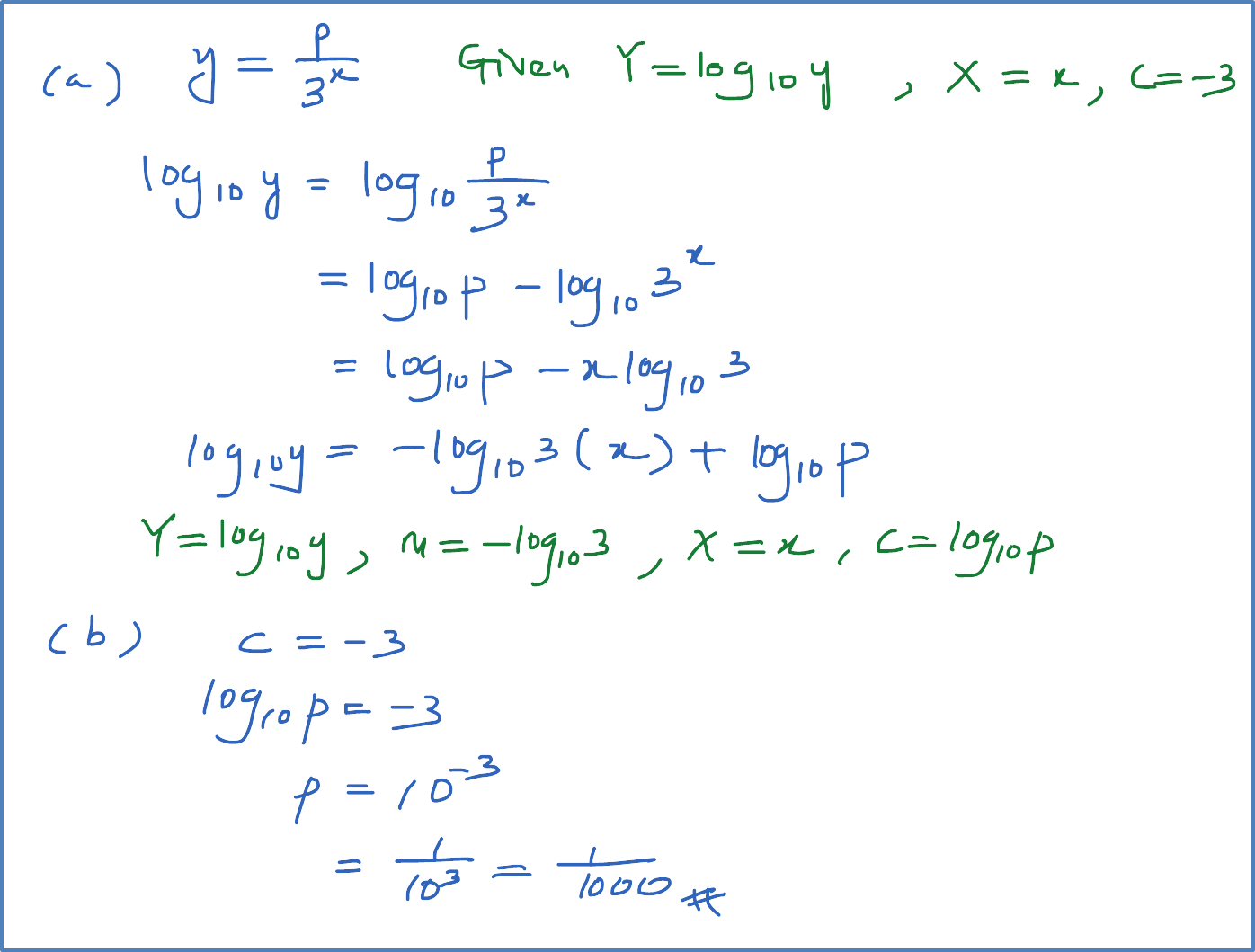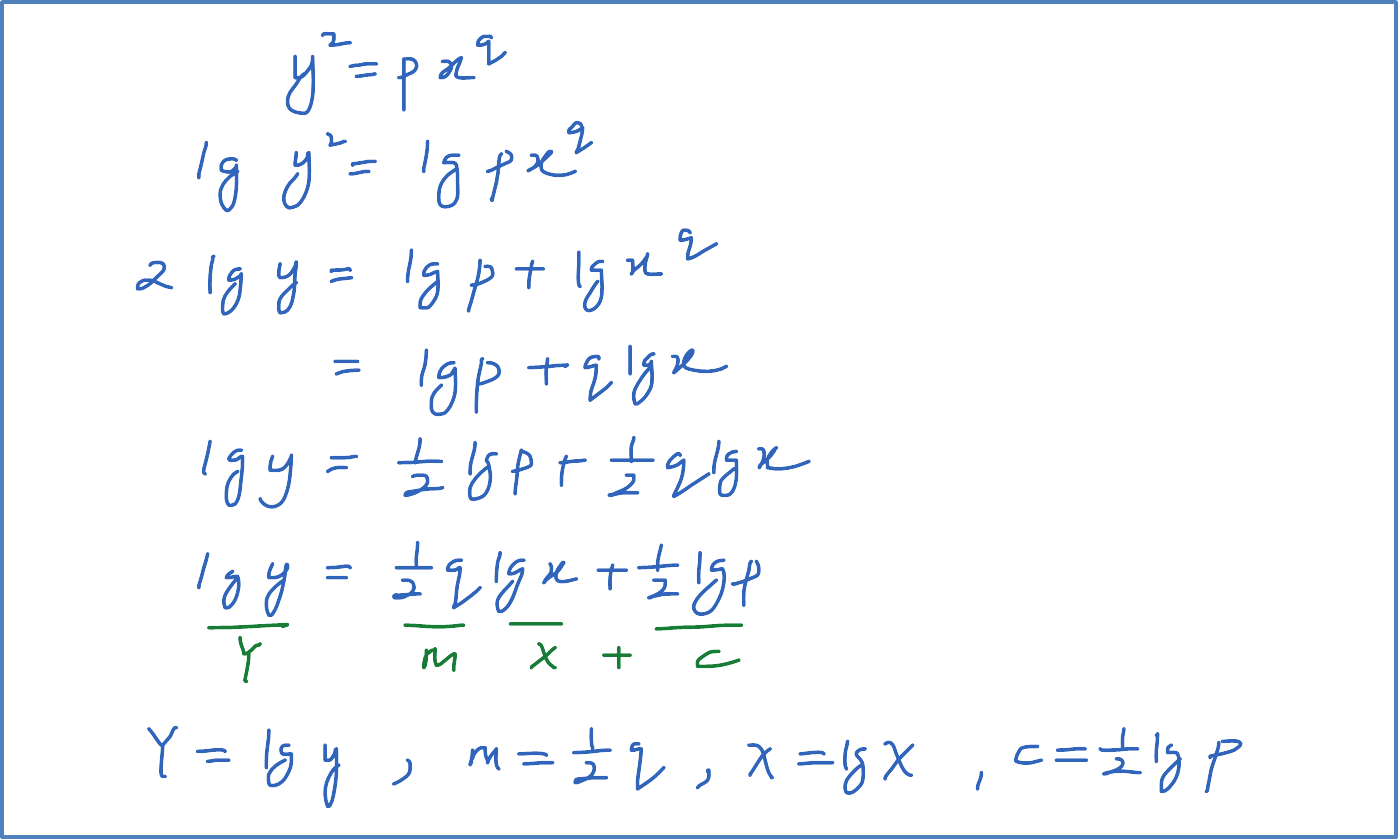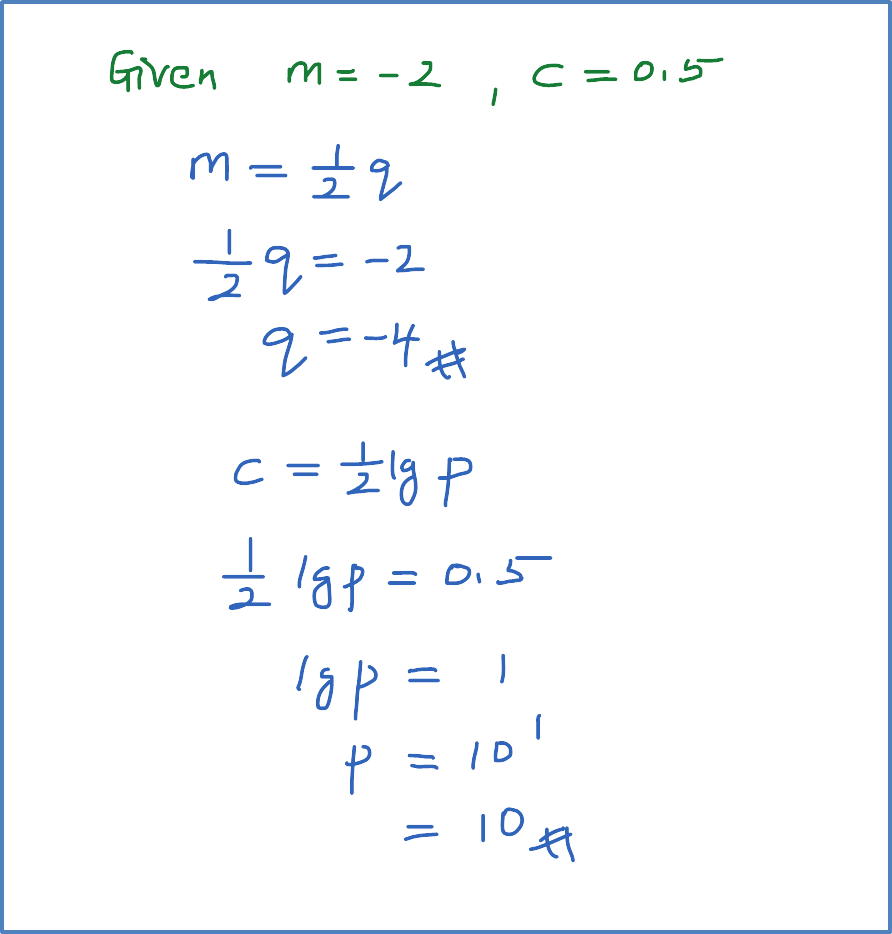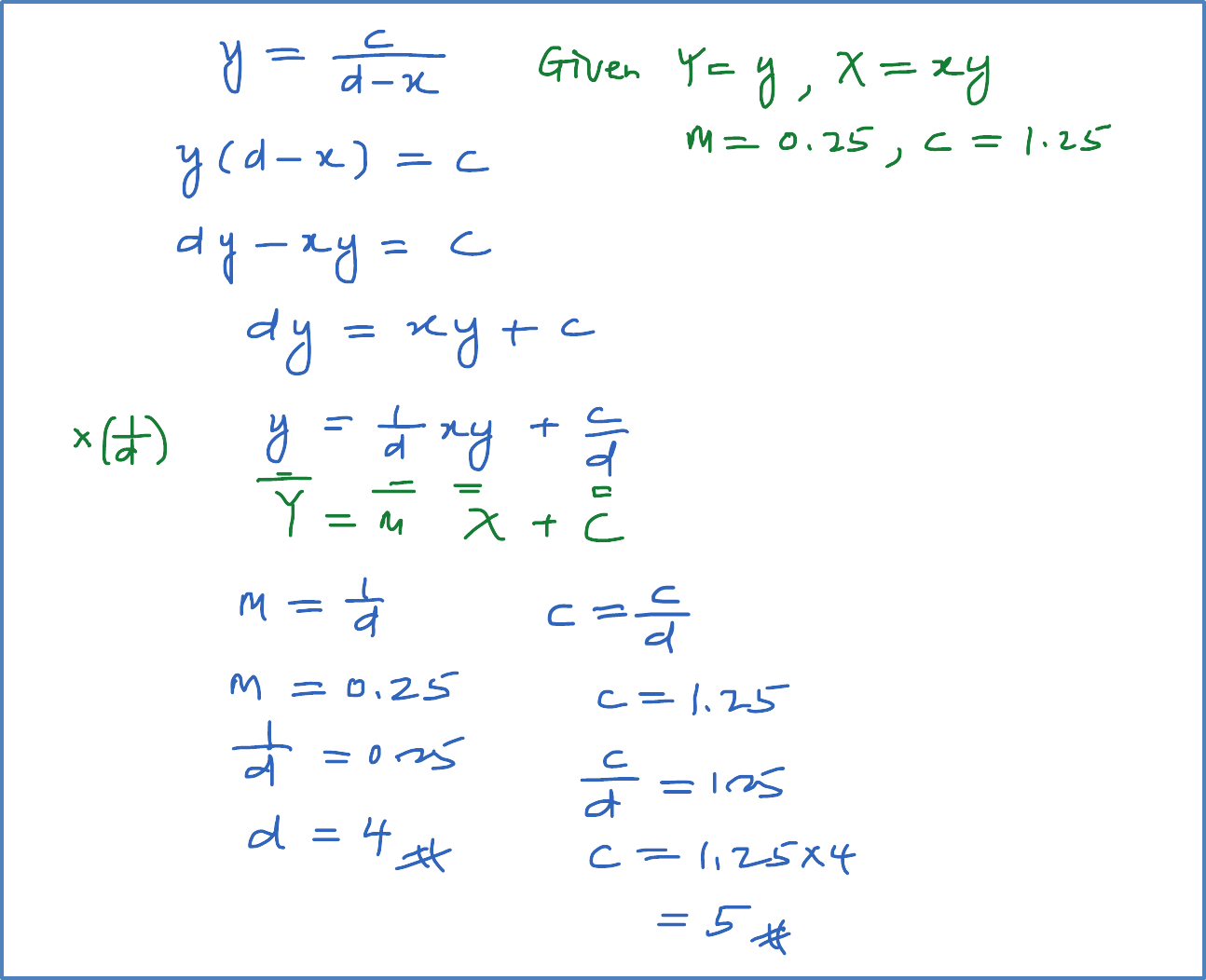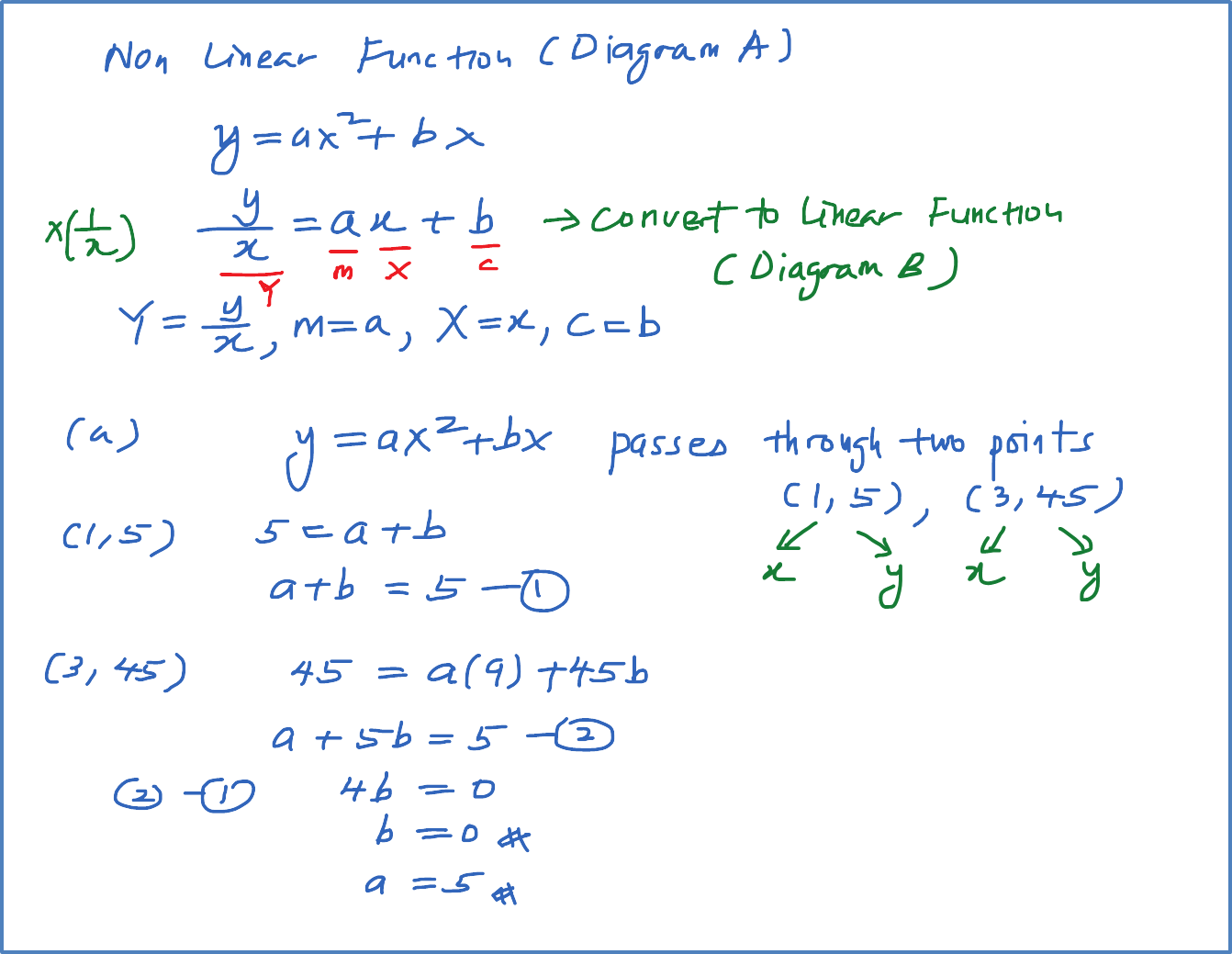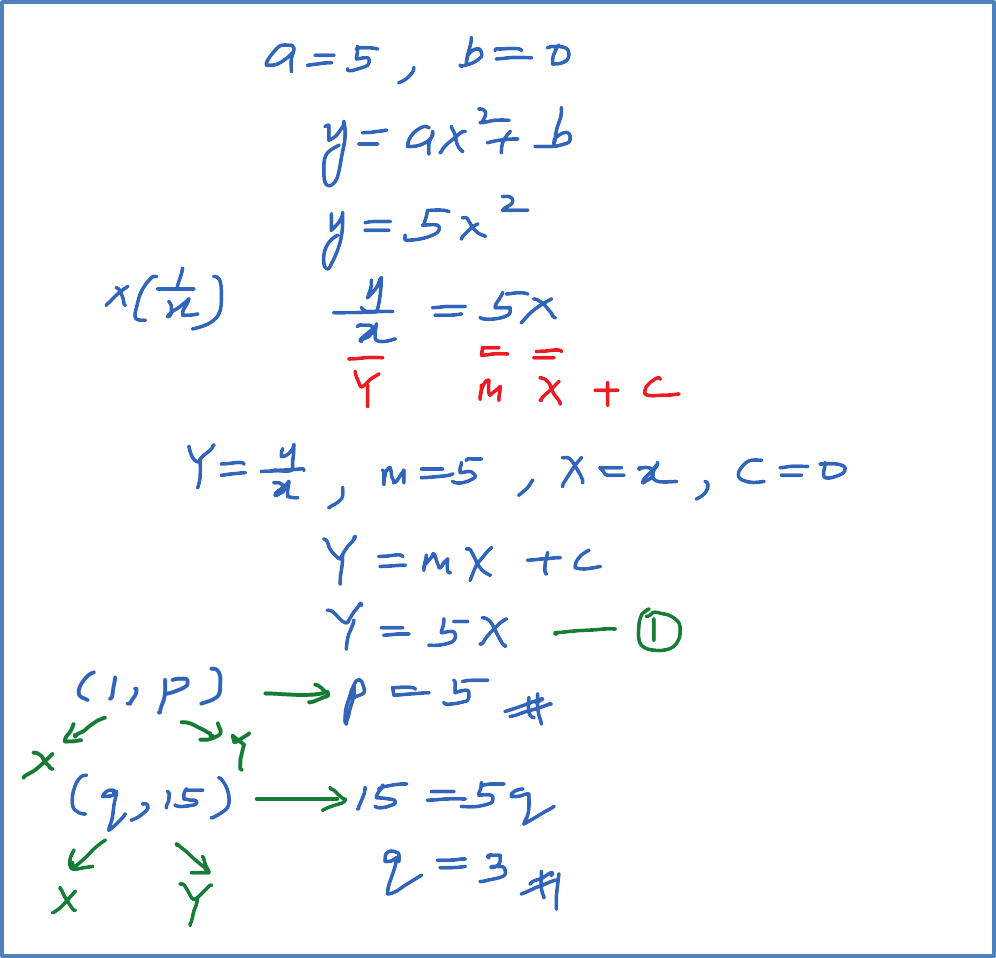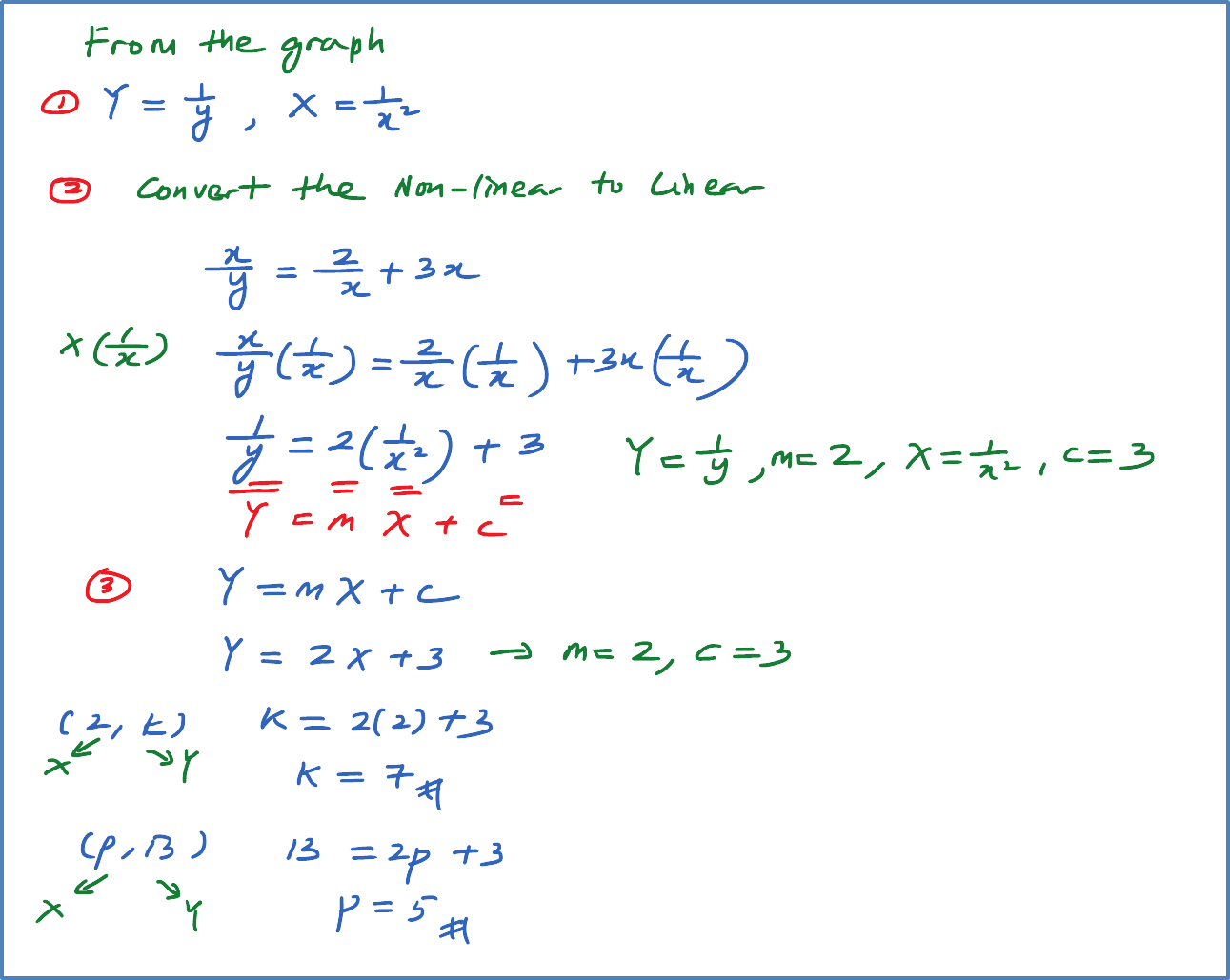Diagram 6 shows the graph of a straight line x2y against 1x.
 Diagram 11
Diagram 11Based on Diagram 6, express y in terms of x.
Solution:
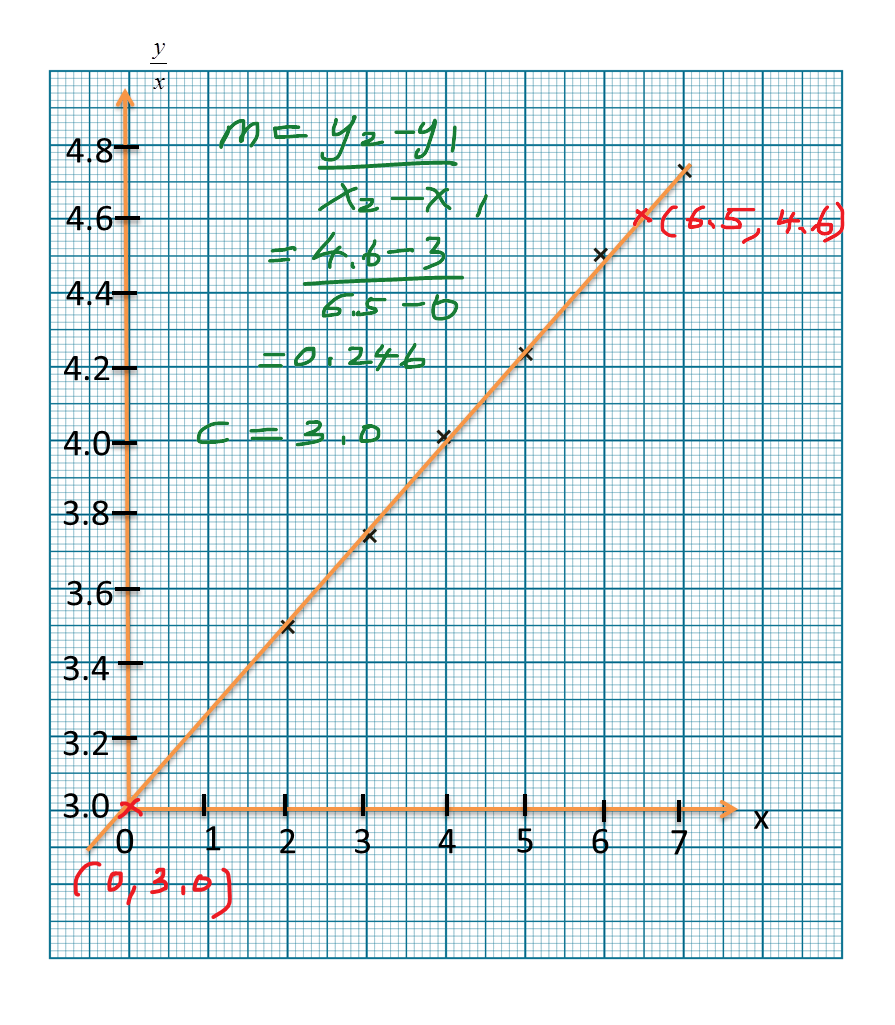
m=4−(−5)6−0=32c=−5Y=x2y, X=1xY=mX+cx2y=32(1x)+(−5)x2y=32x−5x2y=3−10x2xyx2=2x3−10xy=2x33−10x
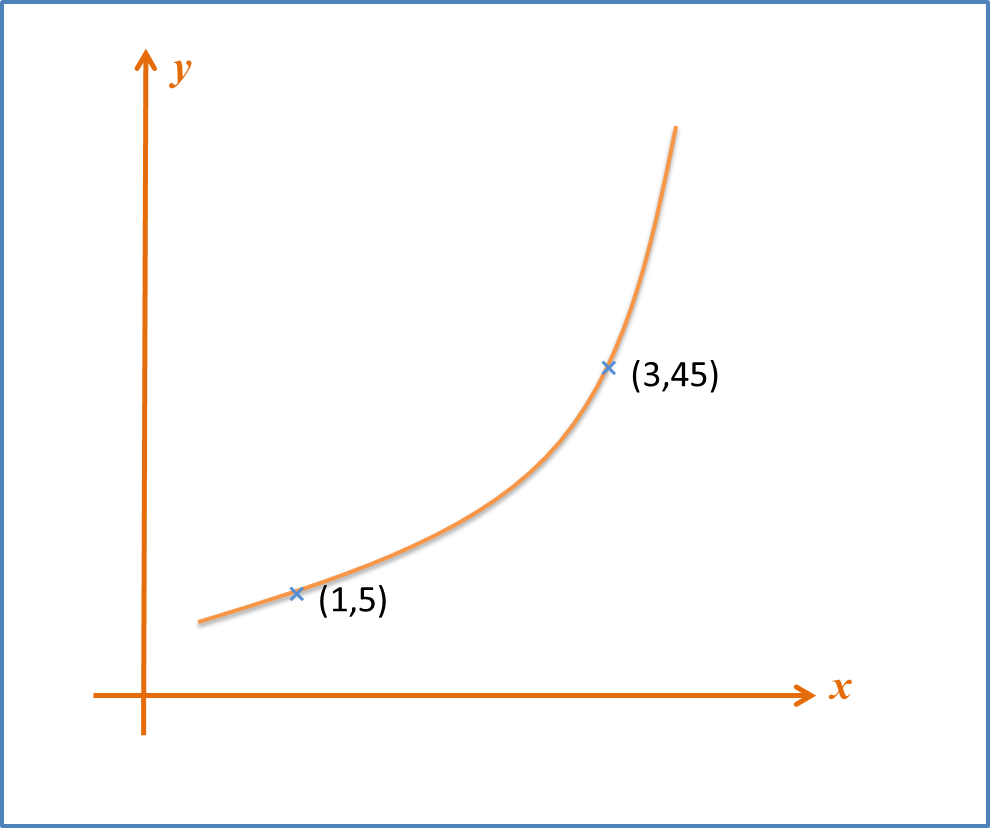
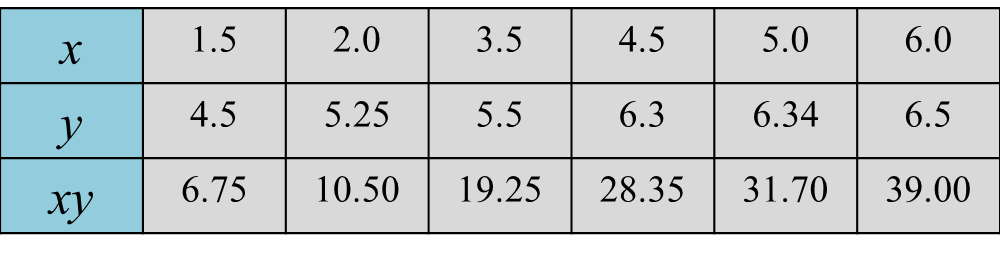
The variables x and y are related by the equation y=x+rx2 , where r is a constant. Diagram 8 shows a straight line graph obtained by plotting (y−x) against 1x2.
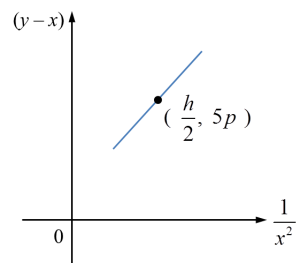 Diagram 12
Diagram 12Express h in terms of p and r.
Solution:
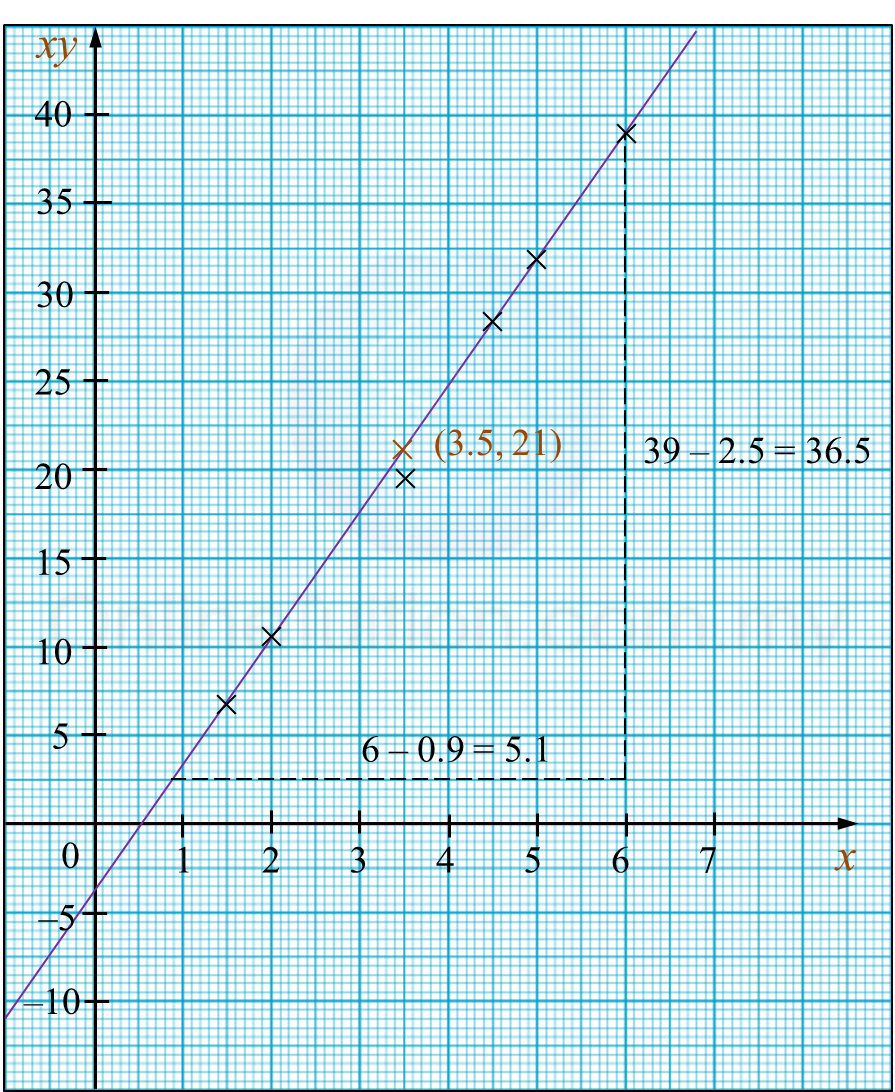
y=x+rx2y−x=r(1x2)+0Y=mX+cm=r, c=0m=y2−y1x2−x1r=5p−0h2−0hr2=5phr=10ph=10pr