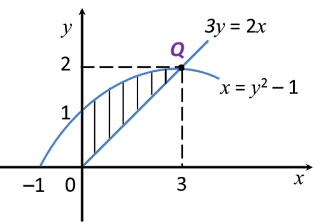
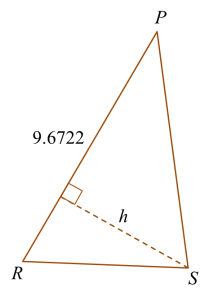
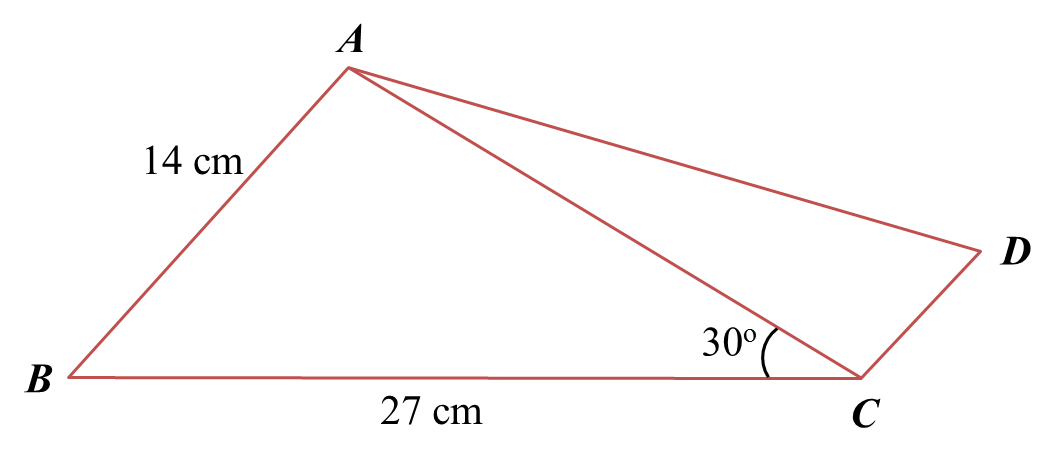
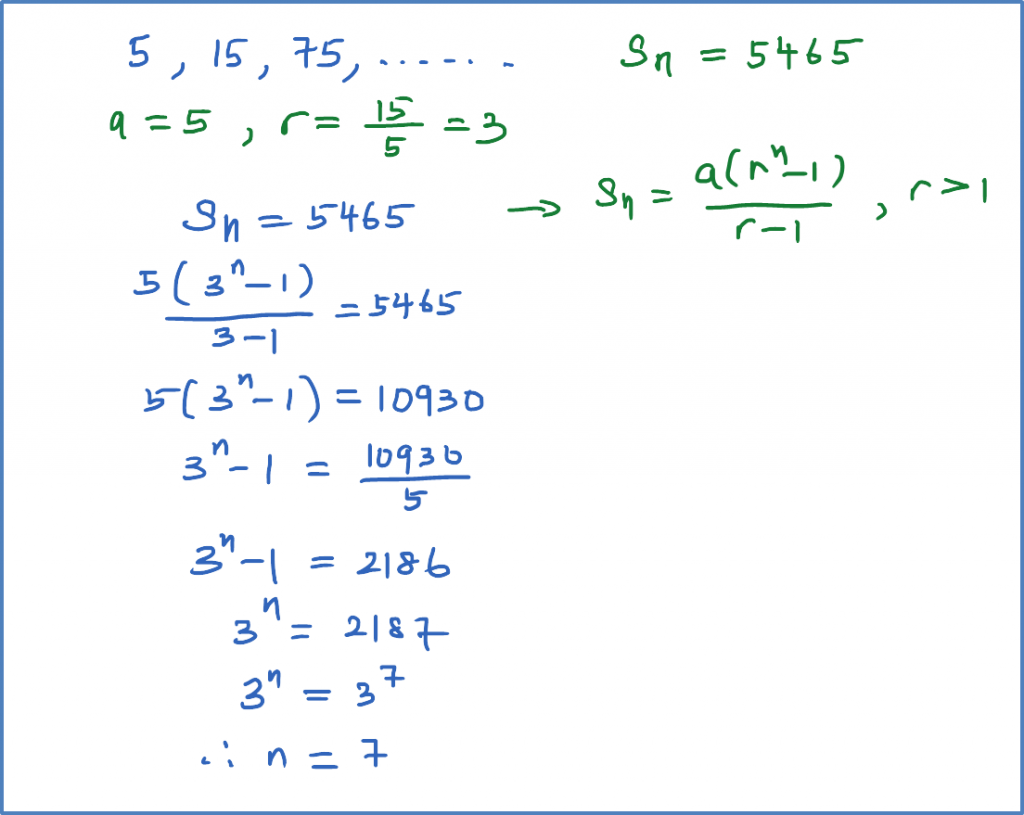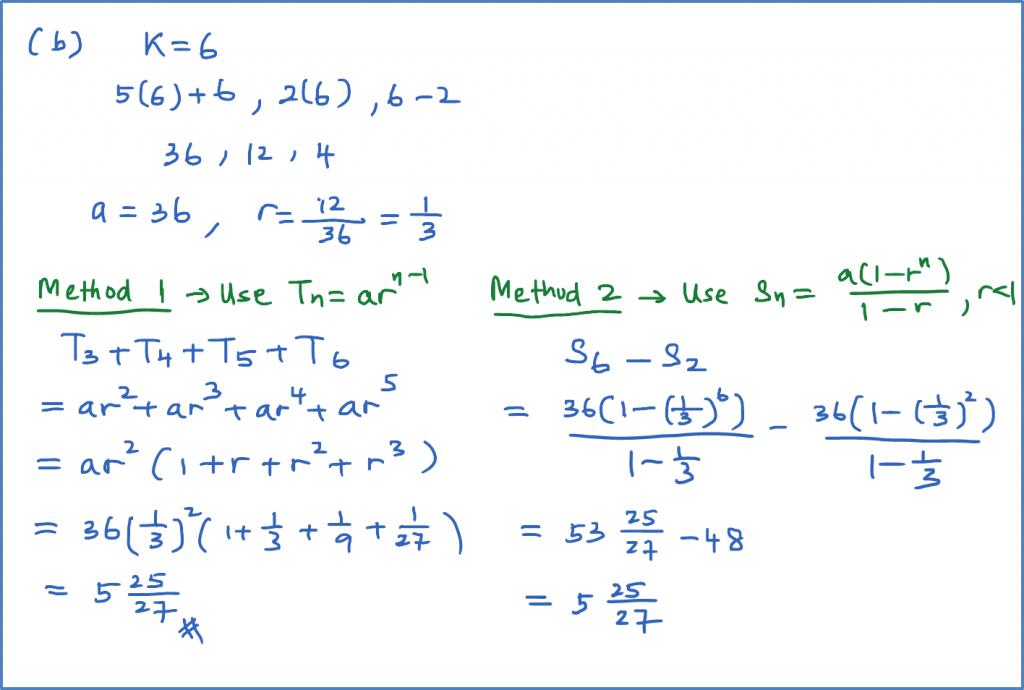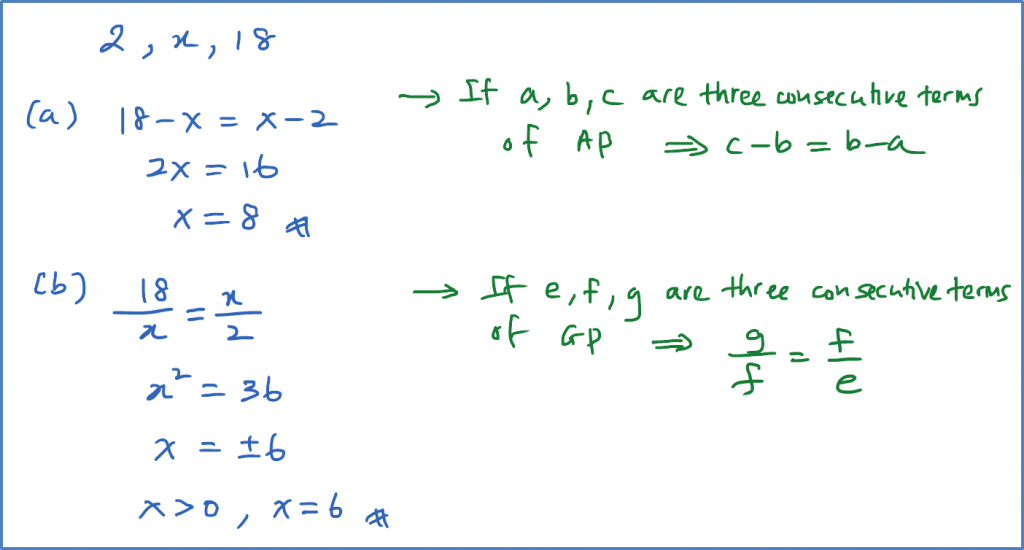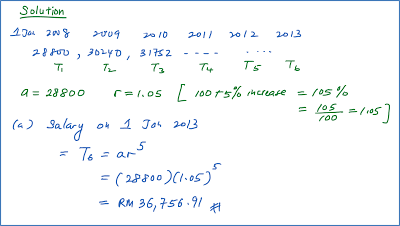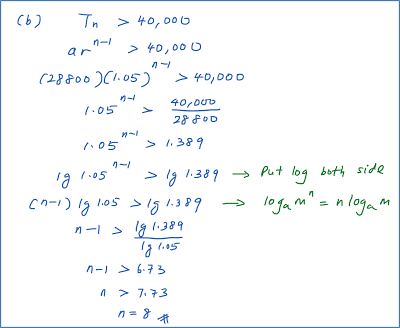Question 8:
Diagram below shows the curve and the straight line y = mx + c. The straight line y = mx + c is a tangent to the curve at (2, 1).

(a) Find the value of m and of c.
(b) Calculate the area of the shaded region.
(c) It is given that the volume generated when the region bounded by the curve, the x–axis and the straight lines x = 2 and x = h is revolved through 360o about the x-axis is
Find the value of h, such that h > 2.
Solution:
(a)
(b)
(c)
Diagram below shows the curve and the straight line y = mx + c. The straight line y = mx + c is a tangent to the curve at (2, 1).

(a) Find the value of m and of c.
(b) Calculate the area of the shaded region.
(c) It is given that the volume generated when the region bounded by the curve, the x–axis and the straight lines x = 2 and x = h is revolved through 360o about the x-axis is
Find the value of h, such that h > 2.
Solution:
(a)
(b)
(c)