1.1 Number Bases (Part 2)

Posted on April 23, 2020 by user

(D) Converting Numbers in Base Two, Eight and Five to Base Ten and Vice Versa

1. Steps to convert numbers in base 2, 8 and 5 to base 10 are as follows.

(a) write the number in expanded notation.

(b) simplify the expanded notation into a single number.

Example 1:

Convert each of the following numbers to a number in base 10.

(a) 10101₂ (b) 1423₈ (c) 324₅

Solution:

(a) 10101₂ = 1 × 2⁴ + 0 × 2³+ 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 21₁₀

(b) 1423₈= 1 × 8³ + 4 × 8²+ 2 × 8¹ + 3 × 8⁰ = 787₁₀

(c) 324₅= 3 × 5² + 2 × 5¹+ 4 × 5⁰ = 89₁₀

Calculator Computation

1. Set the calculator to the ‘BASE’ mode by pressing:

[MODE] [MODE] [3 (BASE)]

2. Set the calculator to the desired number system by pressing:

[BIN] → for base 2

[DEC] → for base 10

[OCT] → for base 8

Key in the following:

(a)

[BIN] 10101 [=] [ DEC ]

The screen display is: [21]

Therefore 10101₂ = 21₁₀

(b)

[OCT] 1423 [=] [ DEC ]

The screen display is: [787]

Therefore 1423₈ = 787₁₀

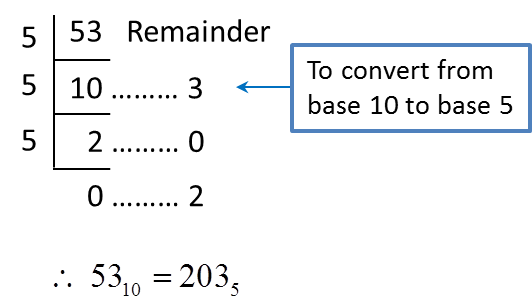
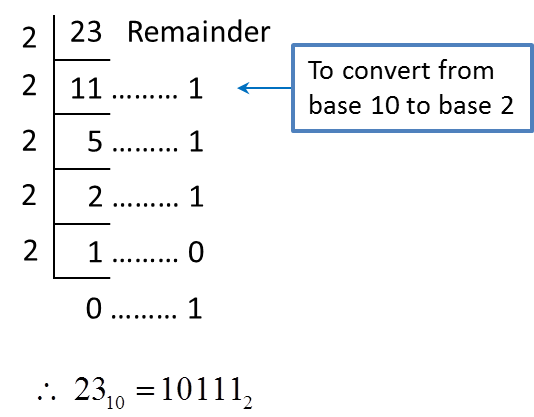
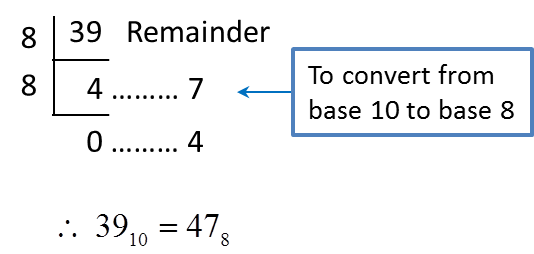
2. Steps to convert a number in base 10 to a number in base 2, 8 and 5 are as follows.

(a) perform repeated division until the quotient is zero.

(b) write the number in new base by referring to the remainders from bottom to the top.

Example 2:

Convert 61₁₀to a number in

(a) Base two (b) base eight (c) base five

Solution:
(a)

(b)

(c)

Calculator Computation

1. Set the calculator to the ‘BASE’ mode by pressing:

[MODE] [MODE] [3 (BASE)]

2. Set the calculator to the desired number system by pressing:

[BIN] → for base 2

[DEC] → for base 10

[OCT] → for base 8

Key in the following:

(a)

[DEC] 61 [=] [ BIN ]

The screen display is: [111101₂]

Therefore 61₁₀ = 111101₂

(b)

[DEC] 61 [=] [ OCT ]

The screen display is: [75]

Therefore 61₁₀ = 75₈

1.1 Number Bases (Part 4)

Posted on April 23, 2020 by user

(F) Addition and Subtraction of Two Numbers in Base Two

1. In the addition of two numbers in base two, the following rules applied:

0₂+ 0₂= 0₂

0₂+ 1₂= 1₂

1₂+ 0₂= 1₂

1₂+ 1₂= 10₂

1₂+ 1₂+ 1₂= 10₂+ 1₂= 11₂

2. In the subtraction of two numbers in base two, the following rules applied:

0₂– 0₂= 0₂

1₂– 0₂= 1₂

1₂– 1₂= 0₂

10₂– 1₂= 1₂

Example 2:

Find the value of each of the following:

(a) 1101₂ + 110₂

(b) 11001₂ + 10100₂

(c) 11011₂ – 1101₂

(d) 1000₂ – 101₂

Solution:

(a)

(b)

(c)

(d)

Calculator Computation

You may obtain the answer directly from a scientific calculator by pressing:

[MODE] [MODE] [3 (BASE)]

Key in the following:

(a)

[ BIN ] 1101 [ + ] 110 [ = ]

The screen display is: [ 10011 ]

(b)

[ BIN ] 11001 [ + ] 11100 [ = ]

The screen display is: [ 110101 ]

(c)

[ BIN ] 11011 [ – ] 1101 [ = ]

The screen display is: [ 1110 ]

(d)

[ BIN ] 1000 [ – ] 101 [ = ]

The screen display is: [ 11 ]

1.1 Number Bases (Part 3)

Posted on April 23, 2020 by user

(E) Converting from One Base to Another

1. The following steps are used to convert a number from one base to another base.

(a) convert the number to a number in base 10 by using expended notation.

(b) use repeated division to convert the number in base 10 to the respective bases.

Example 1:

Convert

(a) 110101₂ to a number in base 5

(b) 43₅ to a number in base 2

(c) 313₈ to a number in base 5

(d) 422₅ to a number in base 8

(e) 100111₂ to a number in base 8
(f) 157₈ to a number in base 2

Solution:

(a) 110101₂

= 1 × 2⁵ + 1 × 2⁴ + 0 × 2³+ 1 × 2² + 0 × 2¹ + 1 × 2⁰

= 53₁₀← (Convert from base 2 to base 10)

(b) 43₅

= 4 × 5¹ + 3 × 5⁰

= 23₁₀← (Convert from base 5 to base 10)

(c) 313₈

= 3 × 8² + 1 × 8¹ + 3 × 8⁰

= 203₁₀← (Convert from base 8 to base 10)

(d) 422₅

= 4 × 5² + 2 × 5¹ + 2 × 5⁰

= 112₁₀← (Convert from base 5 to base 10)

(e) 100111₂

= 1 × 2⁵ + 0 × 2⁴ + 0 × 2³+ 1 × 2² + 1 × 2¹ + 1 × 2⁰

= 39₁₀← (Convert from base 2 to base 10)

(f) 157₈

= 1 × 8² + 5 × 8¹ + 7 × 8⁰

= 111₁₀← (Convert from base 8 to base 10)

Calculator Computation

1. Set the calculator to the ‘BASE’ mode by pressing:

[MODE] [MODE] [3 (BASE)]

2. Set the calculator to the desired number system by pressing:

[BIN] → for base 2

[DEC] → for base 10

[OCT] → for base 8

Key in the following [For (e) and (f) only]:

(e)

[ BIN ] 100111 [ = ] [ OCT ]

The screen display is: [47₈]

Therefore 100111₂ = 47₈

(f)

[ OCT ] 157 [ = ] [ BIN ]

The screen display is: [1101111]

Therefore 157₈ = 1101111₂

10.2 Solving Problems Involving Angle of Elevation and Angle of Depression

Posted on April 23, 2020 by user

Example:

The angle of depression of a cycling kid measured from a hill with 10.9 m high is 52^o. When the kid cycles along the hillside and stops, the angle of depression becomes 25.3^o. What is the distance cycled by the kid along the hillside?

Solution:

Step 1: Draw a diagram to represent the situation.

Step 2: Devise a plan.

Find the lengths of QS and QR. Then, QS – QR = distance cycled by the kid.

$\begin{array}{l} \tan 52^{o} = \frac{10.9}{Q R} \\ Q R = \frac{10.9}{\tan 52^{o}} \\ Q R = 8.5 m \end{array}$

$\begin{array}{l} \tan {25.3}^{o} = \frac{10.9}{Q S} \\ Q S = \frac{10.9}{\tan {25.3}^{o}} \\ Q S = 23.1 m \end{array}$

QS – QR = (23.1 – 8.5) m = 14.6 m

Therefore the kid has cycled 14.6 metres.

SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 1:

Diagram below shows two vertical poles on a horizontal plane. J, K, L, M and N are five points on the poles such that KL = MN.

Name the angle of elevation of point J from point M.

Solution:

Angle of elevation of point J from point M = ∠KMJ

Question 2:

Diagram below shows two vertical poles JM and KL, on a horizontal plane.

The angle of depression of vertex K from vertex J is 42^o.

Calculate the angle of elevation of vertex K from M.

Solution:

JN = 10 tan 42^o = 9.004 m

NM = 25 – 9.004 = 15.996 m

KL = NM = 15.996 m

$\begin{array}{l} \tan ∠ K M L = \frac{K L}{M L} \\ = \frac{15.996}{10} \\ = 1.5996 \\ ∠ K M L = \tan^{- 1} 1.5996 \\ = 57^{o} 59^{'} \end{array}$

Question 3:

Diagram below shows a vertical pole KMN on a horizontal plane. The angle of elevation of M from L is 20^o.

Calculate the height, in m, of the pole.

Solution:

$\begin{array}{l} \tan 20^{o} = \frac{K M}{K L} \\ 0.3640 = \frac{K M}{15} \\ K M = 5.4 m \\ Height of the pole = 9 + 5.4 = 14.4 m \end{array}$

10.1 Angle of Elevation and Angle of Depression (Part 1)

Posted on April 23, 2020 by user

10.1 Angle of Elevation and Angle of Depression (Part 1)

1. Angle of elevation is the acute angle measured from a horizontal line up to the line of sight.

Example 1:

Angle of elevation of object O from P = ∠OPA

2. Angle of depression is the acute angle measured down from a horizontal line to the line of sight.

Example 2:

Angle of depression of object O from P = ∠OPA

SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 4:

Diagram below shows three vertical poles JP, KN and LM, on a horizontal plane.

The angle of elevation of N from P is 15^o.

The angle of depression of M from N is 35^o.

Calculate the distance, in m, from K to L.

Solution:

$\begin{array}{l} \tan ∠ A P N = \frac{A N}{P A} \\ \tan 15^{o} = \frac{A N}{4} \\ A N = 4 \times 0.268 \\ A N = 1.072 m \\ Length of B N = 2 + 1.072 = 3.072 c m \\ \tan ∠ B M N = \frac{B N}{B M} \\ \tan 35^{o} = \frac{3.072}{B M} \\ B M = \frac{3.072}{0.700} = 4.389 \\ Distance of K L = 4.389 m \end{array}$

Question 5:

Diagram below shows two vertical poles JM and LN, on a horizontal plane.

The angle of elevation of M from K is 70^oand the angle of depression of K from N is 40^o.

Find the difference in distance, in m, between JK and KL.

Solution:

$\begin{array}{l} \tan ∠ J K M = \frac{14}{J K} \\ J K = \frac{14}{\tan 70^{o}} \\ J K = 5.096 m \\ \tan ∠ L K N = \frac{8}{K L} \\ K L = \frac{8}{\tan 40^{o}} \\ K L = 9.534 m \\ Difference in distance of J K and K L \\ = 9.534 - 5.096 \\ = 4.438 m \end{array}$

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 7:

Which graph represents y = sin x for 0^o ≤ x ≤ 270^o?

Solution:

Answer: B

Question 8:

Which graph represents y = sin x for 0^o ≤ x ≤ 180^o?

Solution:

Answer: D

Question 9:

Which graph represents part of y = sin x?

Solution:

Answer: A

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 1:

In the diagram above, find the value of tan θ.

Solution:

$\begin{array}{l} In △ A B C, using Pythagoras' Theorem, \\ A C = \sqrt{1^{2} + 1^{2}} = \sqrt{2} c m \\ \tan θ = \frac{C D}{A C} \\ \tan θ = \frac{1}{\sqrt{2}} \end{array}$

Question 2:

In the diagram above, ABCE is a rectangle and point D lies on the straight line EC. Given that DC = 5 cm and AE = 4cm, find the value of cosθ.

Solution:

$\begin{array}{l} A D = D C = 5 c m \\ In △ A E D, using Pythagoras' Theorem, \\ E D = \sqrt{5^{2} - 4^{2}} = 3 c m \\ \cos θ = - \cos ∠ A D E \leftarrow \begin{array}{l} Since 90^{\circ} < θ < 180^{\circ} \\ (in quadrant II), \cos θ is negative \end{array} \\ \cos θ = - \frac{E D}{A D} \\ \cos θ = - \frac{3}{5} \end{array}$

Question 3:

In the diagram above, PMR is a straight line, M is the midpoint of line PR. Given that QR = 12cm and sin y°= 0.6, find the value of tan x°.

Solution:

$\begin{array}{l} In triangle Q M R, \\ \sin y^{\circ} = 0.6 \\ \sin y^{\circ} = \frac{Q R}{Q M} = \frac{6}{10} \\ Given Q R = 12 c m, ∴ Q M = 10 \times 2 = 20 c m \\ In △ Q M R, using Pythagoras' Theorem, \\ M R = \sqrt{20^{2} - 12^{2}} = 16 c m \\ P R = 16 \times 2 = 32 c m \\ Hence \tan x^{\circ} = \frac{Q R}{P R} = \frac{12}{32} = \frac{3}{8} \end{array}$