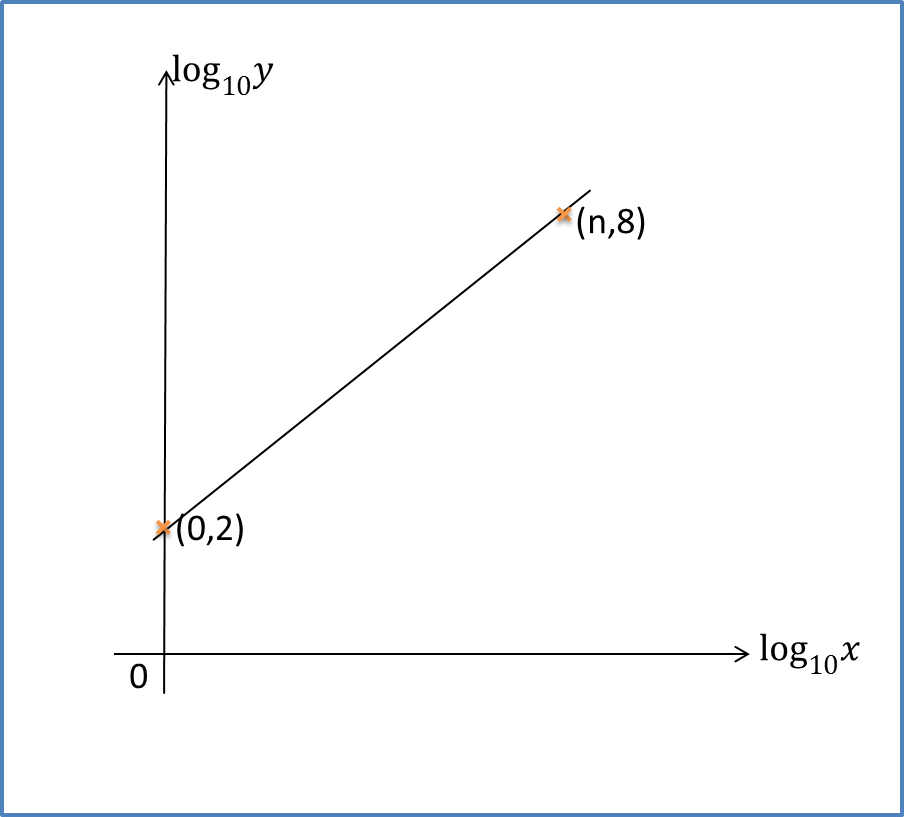
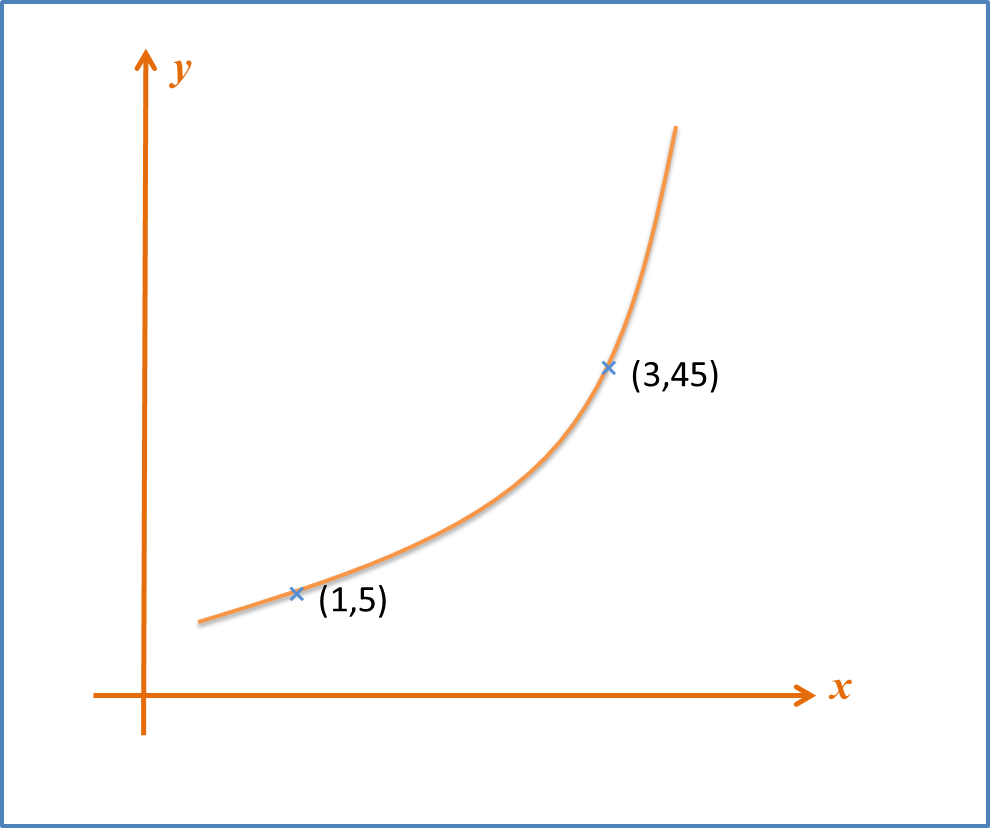
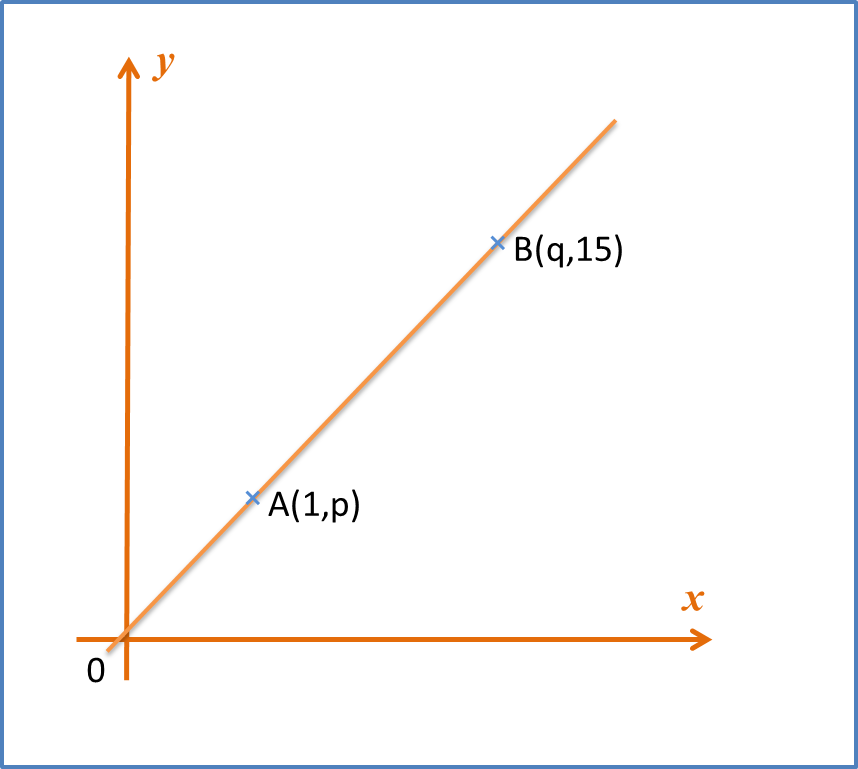
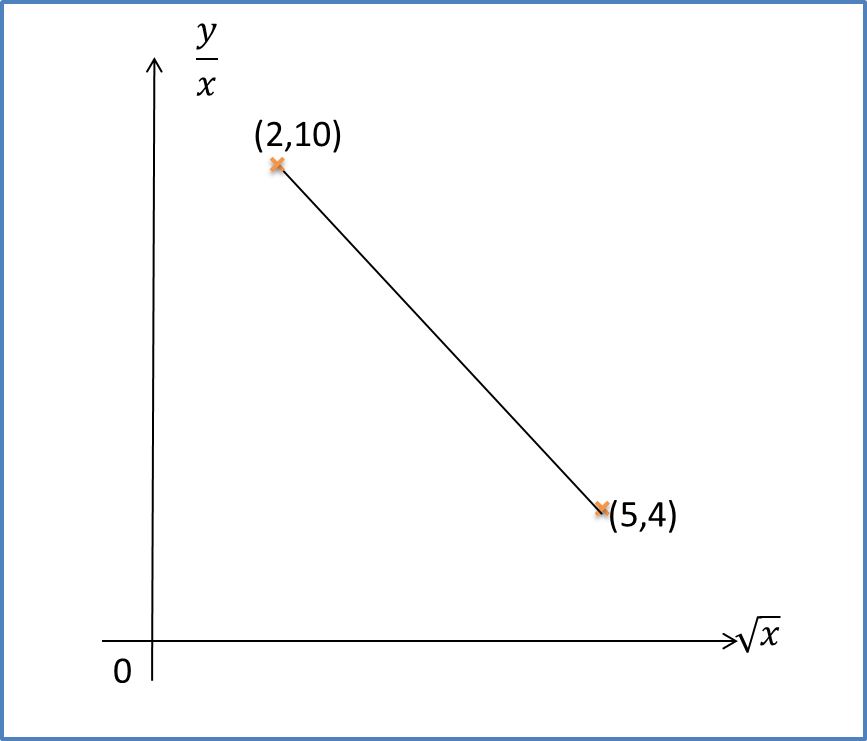
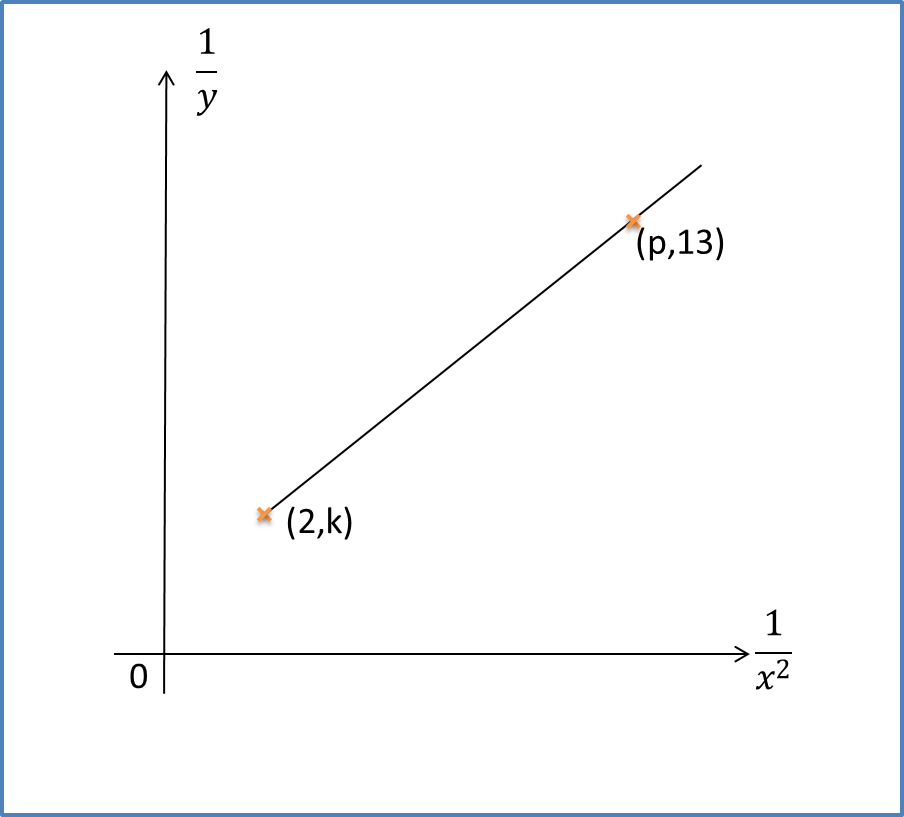
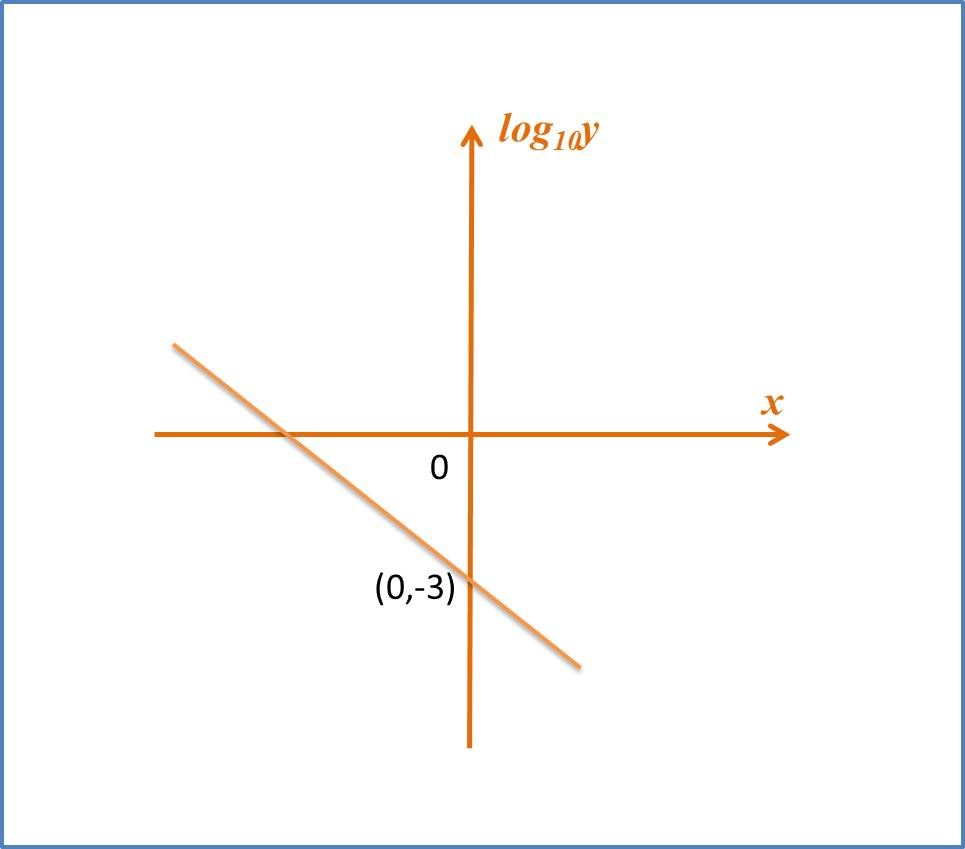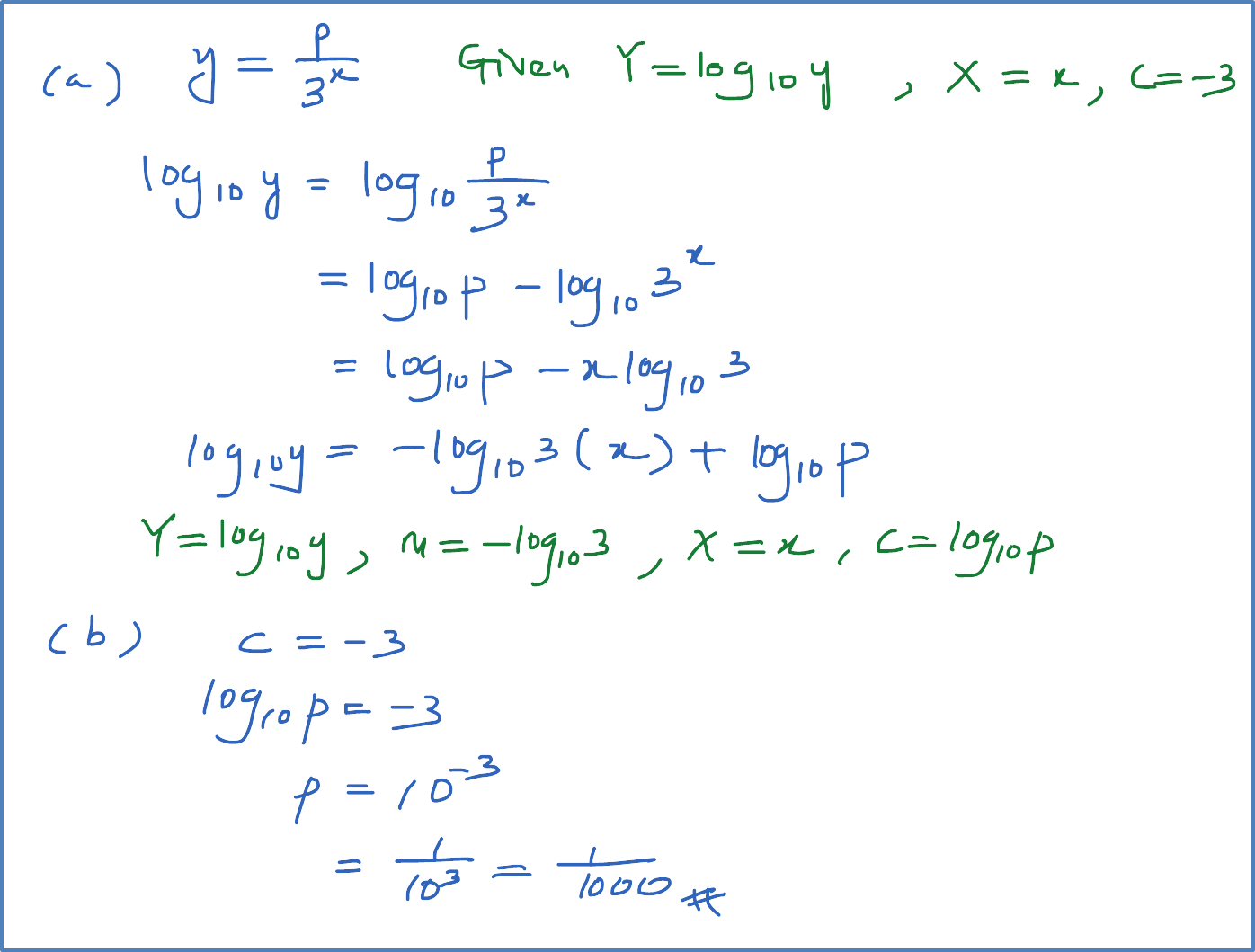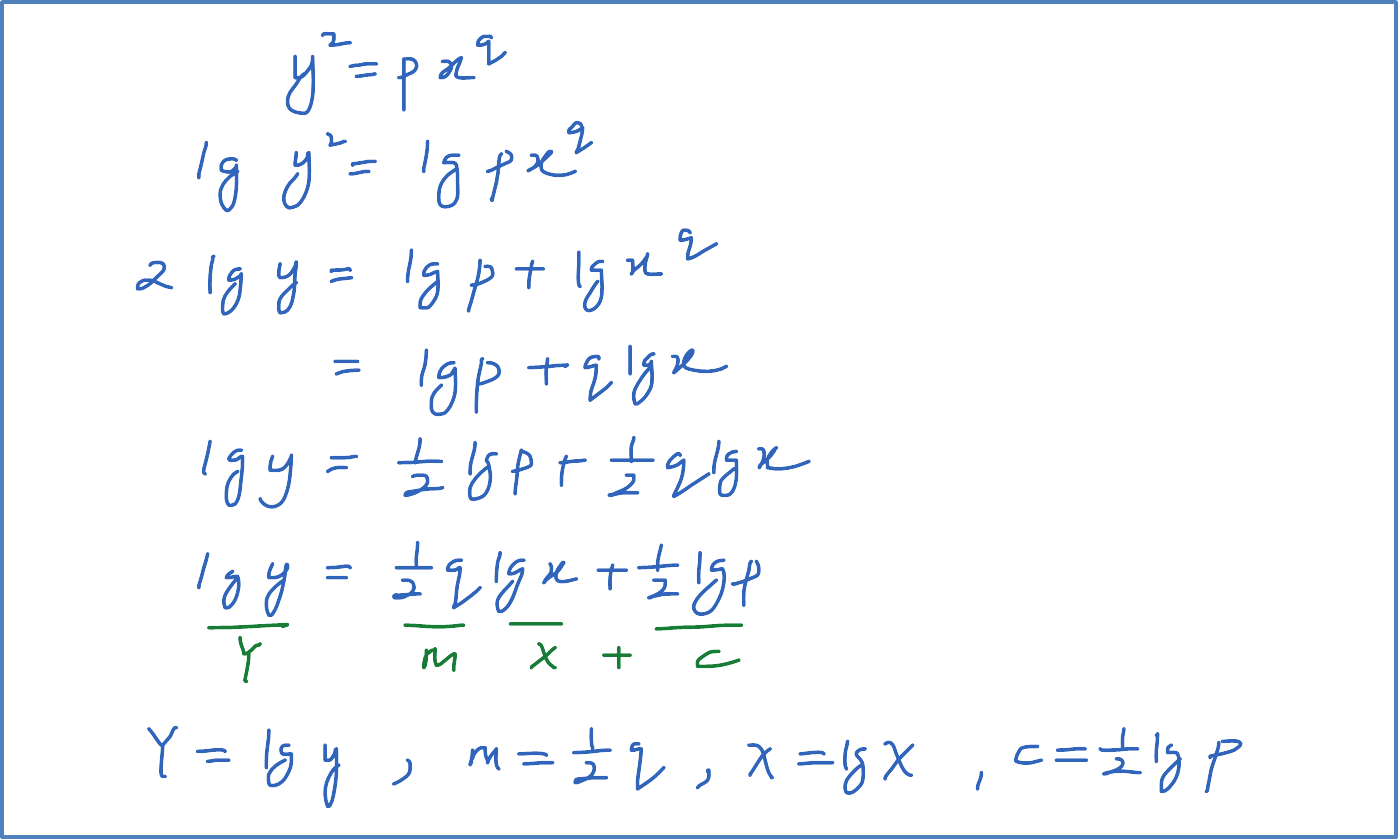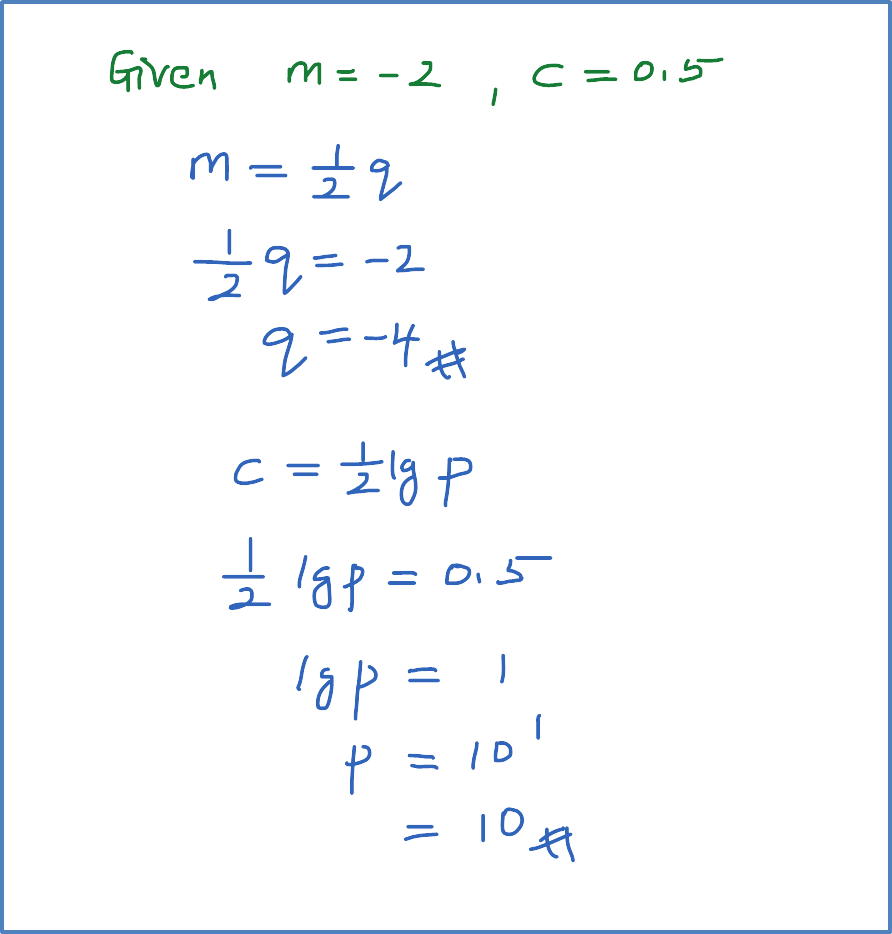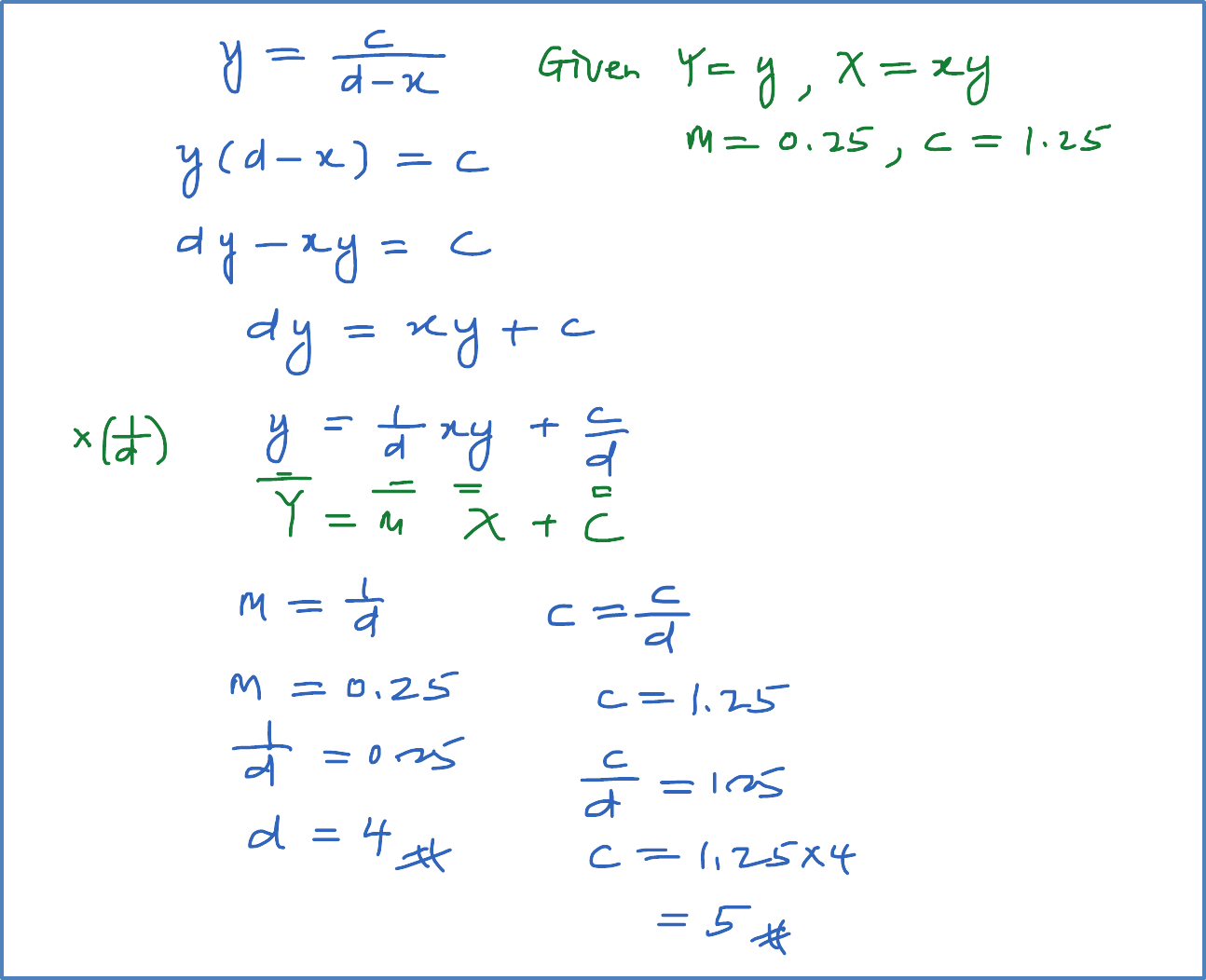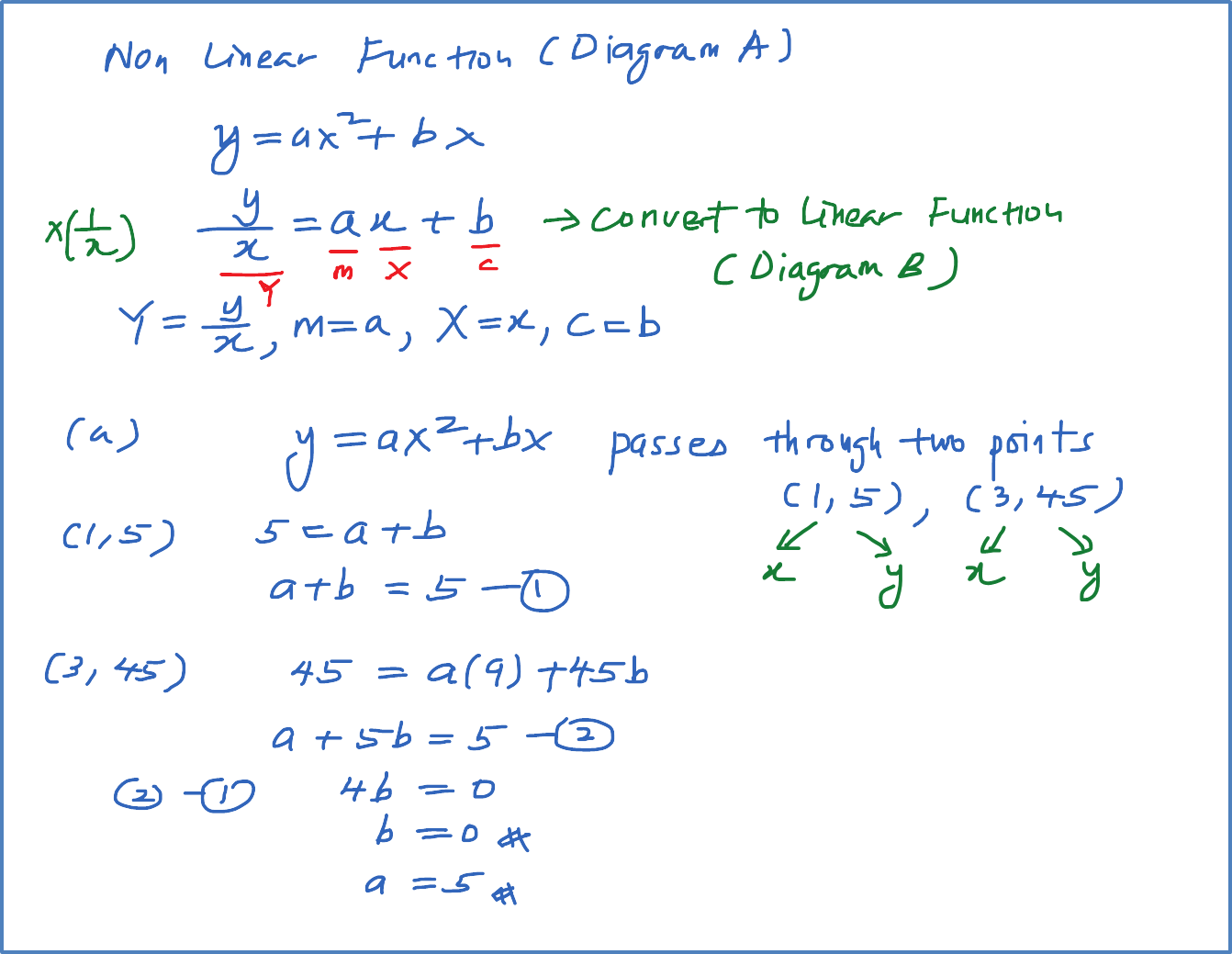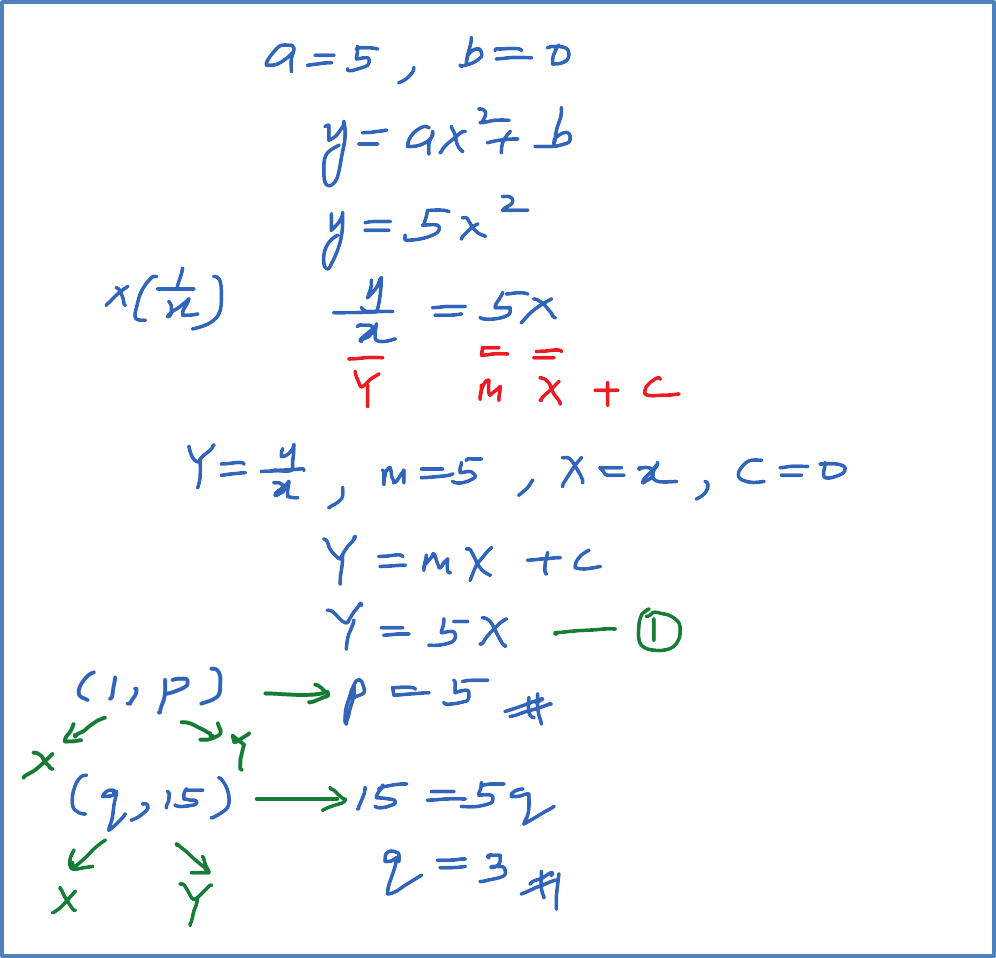Example 3:
The volume of water in a tank is 75 litres on the first day. Subsequently, 15 litres of water is added to the tank everyday.
Calculate the volume, in litres, of water in the tank at the end of the 12th day.
Solution:
Volume of water on the first day = 75l
Volume of water on the second day = 75 + 15 = 90l
Volume of water on the third day = 90 + 15 = 105l
75, 90, 105, …..
AP, a = 75, d = 90 – 75 = 15
Volume of water on the 12th day,
T12 = a + 11d
T12 = 75 + 11 (15)
T12 = 240l
Example 4:
The first three terms of an arithmetic progression are 72, 65 and 58.
The nth term of this progression is negative.
Find the least value of n.
Solution:
72, 65, 58
AP, a = 72, d = 65 – 72 = –7
The nth term is negative,
Tn < 0
a + (n – 1) d < 0
72 + (n – 1) (–7) < 0
(n – 1) (–7) < –72
n – 1 > –72/ –7
n – 1 > 10.28
n > 11.28
n must be integer, n = 12, 13, 14, ….
Therefore, the least value of n = 12.