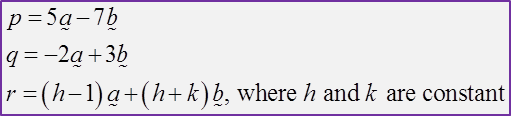SPM Add Maths
5.3.4 Sketching Graphs of Trigonometric Functions (Part 3)
5.3.4 Sketching Graphs of Trigonometric Functions (Part 3)
Example 2:
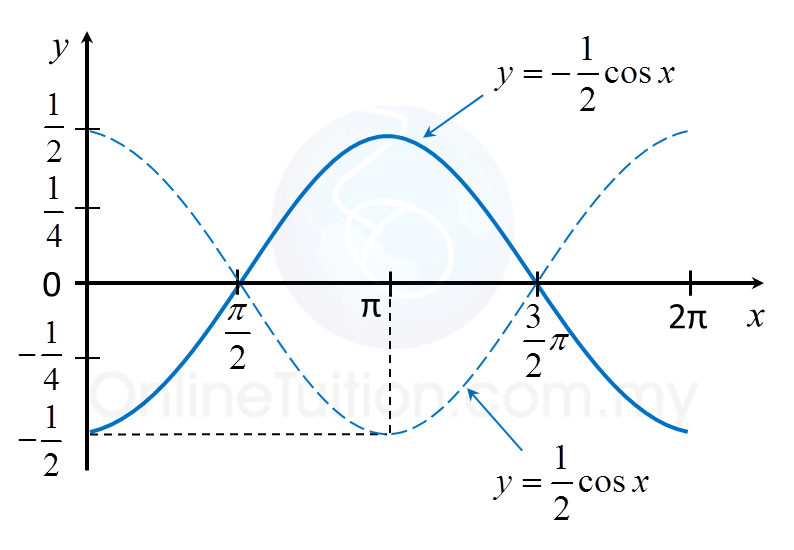
(a) Sketch the graph y = –½ cos x for 0 ≤ x ≤ 2π.
(b) Hence, using the same axes, sketch a suitable graph to find the number of solutions to the equation
π2x+cosx=0
for 0 ≤ x ≤ 2π.
State the number of solutions.
Solution:
(a)

(b)
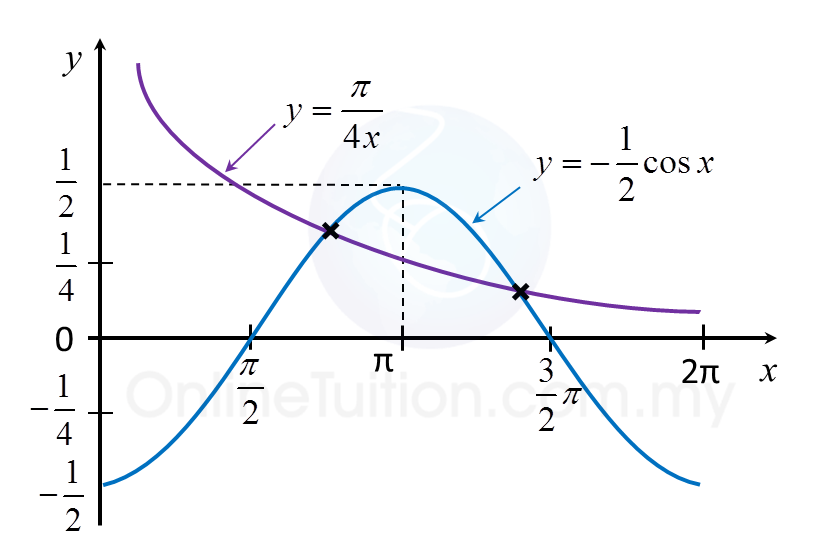

π2x+cosx=0π2x=−cosxπ4x=−12cosx←Multiply both sides by12y=π4x←y=−12cosx
The suitable graph to draw is y=π4x.
x |
π2
|
π |
2π |
y=π4x
|
½ |
¼ |
⅛ |
From the graphs, there are two points of intersection for 0 ≤ x ≤ 2π.
Number of solutions = 2.
5.3.2 Sketching Graphs of Trigonometric Functions (Part 1)
5.3.2 Sketching Graphs of Trigonometric Functions
Example 1:
Sketch the graph of each of the following trigonometric functions for π ≤ x ≤ 2π.
(a) y = 3 sin x
(b) y = 2 cos x
(b) y = 2 cos x
(c) y = sin x + 1
(d) y = cos x –1
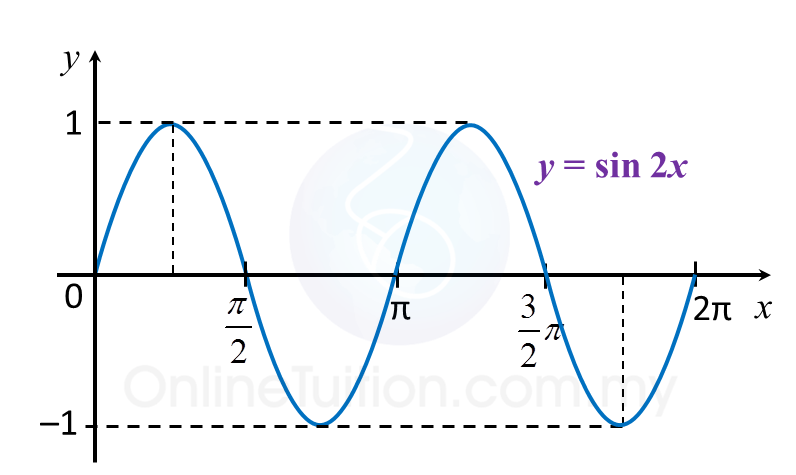
(e) y = sin 2x
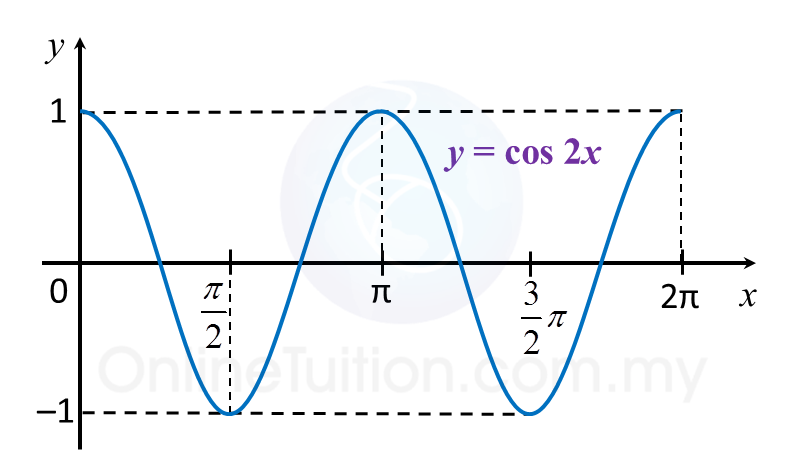
(f) y = cos 2x


(d) y = cos x –1
(e) y = sin 2x
(f) y = cos 2x
Solution:
(a)
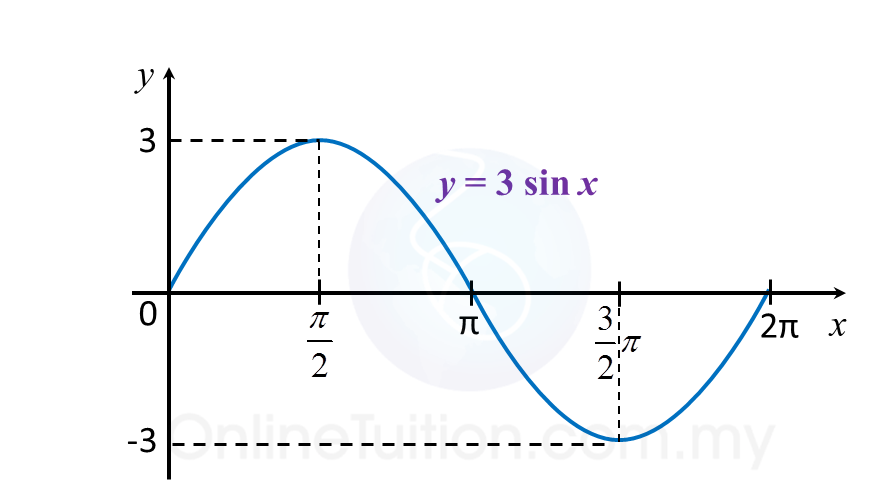
(a)

(b)
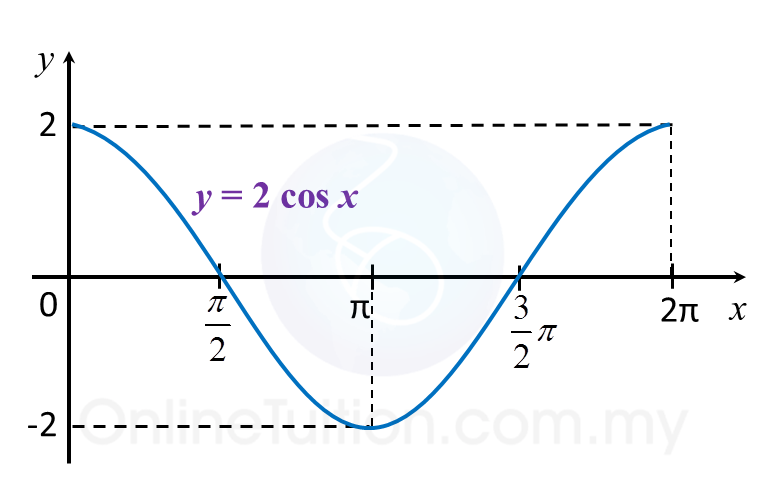

(c)

(d)

(e)

(f)

Basic Trigonometric Identities
5.4 Basic Trigonometric Identities
Three basic trigonometric identities are:
Three basic trigonometric identities are:
sin2 x + cos2 x = 1
tan2 x + 1 = sec2 x
cot2 x + 1 = cosec2 x
|
[adinserter block="3"]
Example 1 (To Prove Trigonometric Identities which involve the Three Basic Identities)
Prove each of the following trigonometric identities.
(a) sin2 x – cos2 x = 1 – 2 cos2 x
(b) (1 – cosec2 x) (1– sec2 x) = 1
Solution:
(a)
sin2 x– cos2 x = 1 – 2 cos2x
LHS: sin2 x – cos2 x
= 1 – cos2 x – cos2 x
= 1 – 2 cos2 x (RHS)
(b)
(1−cosec2x)(1−sec2x)=1LHS:(1−cosec2x)(1−sec2x)=(−cot2x)(−tan2x)=(cot2x)(tan2x)=(1tan2x)tan2x=1(RHS)
Example 2 (To Solve Trigonometric Equations which involve the Three Basic Identities)
Solve the following trigonometric equations for 0o≤ x ≤ 360o.
(a) sin2 x cos x + 1 = cos x
(b) 2 cosec2 x – 5 cot x = 0
Solution:
(a)
sin2 x cos x + 1 = cos x
(1 – cos2 x) cos x + 1 = cos x
cos x – cos3 x + 1 = cos x
cos3 x = 1
cos x = 1
x = 0o, 360o
(b)
2 cosec2 x – 5 cot x = 0
2 (1 + cot2 x) – 5 cot x = 0
2 + 2 cot2 x – 5 cot x = 0
2 cot2 x – 5 cot x + 2 = 0
(2 cot x – 1) (cot x – 2) = 0
cot x= ½ or cotx = 2
cot x= ½ or cot x = 2
tan x = 2 tan x = ½
x =63.43o, 243.43o x = 26.57o, 206.57o
(Note: tangent is positive in the first and third quadrants)
Thus, x = 26.57o, 63.43o, 206.57o, 243.43o
Short Question 6 & 7
Question 6:
The points P, Q and R are collinear. It is given that →PQ=4a˜−2b˜ and →QR=3a˜+(1+k)b˜ , where k is a constant. Find
(a) the value of k,
(b) the ratio of PQ : QR.
Solution:
(a)
Note: If P, Q and R are collinear,→PQ=m→QR4a˜−2b˜=m[3a˜+(1+k)b˜]4a˜−2b˜=3ma˜+m(1+k)b˜Comparing vector:a˜: 4=3m m=43b˜: −2=m(1+k)−2=43(1+k)1+k=−64k=−32−1k=−52
(b)
→PQ=m→QR→PQ=43→QR→PQ→QR=43∴
The points P, Q and R are collinear. It is given that →PQ=4a˜−2b˜ and →QR=3a˜+(1+k)b˜ , where k is a constant. Find
(a) the value of k,
(b) the ratio of PQ : QR.
Solution:
(a)
Note: If P, Q and R are collinear,→PQ=m→QR4a˜−2b˜=m[3a˜+(1+k)b˜]4a˜−2b˜=3ma˜+m(1+k)b˜Comparing vector:a˜: 4=3m m=43b˜: −2=m(1+k)−2=43(1+k)1+k=−64k=−32−1k=−52
(b)
→PQ=m→QR→PQ=43→QR→PQ→QR=43∴
Question 7:
Given that and , find the values of m if the vector is parallel to the vector .
Solution:
Given that and , find the values of m if the vector is parallel to the vector .
Solution:
4.2 Multiplication of Vector by a Scalar and the Parallel Condition of Two Vectors
4.2 Multiplication of Vector by a Scalar and the Parallel Condition of Two Vectors
1. When a vector
is multiplied by a scalar k, the product is
. Its magnitude is k times the magnitude of the vector
.
2. The vector is parallel to the vector if and only if , where k is a constant.
3. If the vectors
and
are not parallel and
, then h = 0 and k = 0.
Example 1:
If vectors
are not parallel and
, find the value of k and of h.
Solution:
The vectors
are not parallel, so
k – 7 = 0 → k = 7
5 + h = 0 → h = –5
4.3 Addition and Subtraction of Vectors
4.3.2 Subtraction of Vectors
The subtraction of the vector
from the vector
is written as
. This operation can be considered as the addition of the vector
with the negative vector of
. Therefore
Example 1:
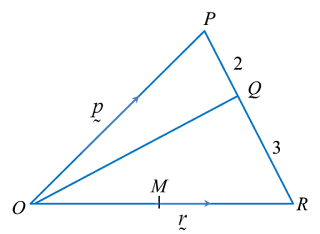
In the diagram above, vector and Q divides PR in the ratio of 2 : 3. Find the following vectors in terms of
Solution:
(a)
(b)
(c)
Long Question 5
Question 5:
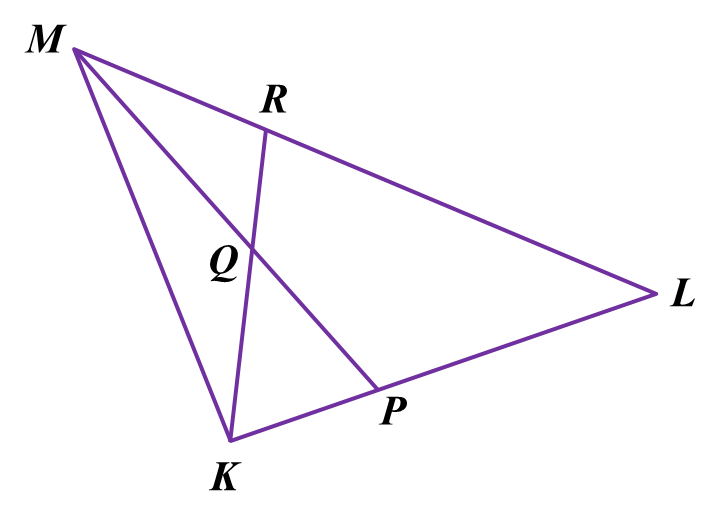
Diagram below shows a triangle KLM.
Solution:
(a)(i)
(a)(ii)
(b)
(c)
Diagram below shows a triangle KLM.

Solution:
(a)(i)
(a)(ii)
(b)
(c)
Short Question 4 & 5
Long Question 2
Question 2:
Given that and , find
(a) the coordinates of A,
(b) the unit vector in the direction of .
(c) the value of m if CD is parallel to AB .
Solution:
(a)
(b)
(c)
Given that and , find
(a) the coordinates of A,
(b) the unit vector in the direction of .
(c) the value of m if CD is parallel to AB .
Solution:
(a)
(b)
(c)