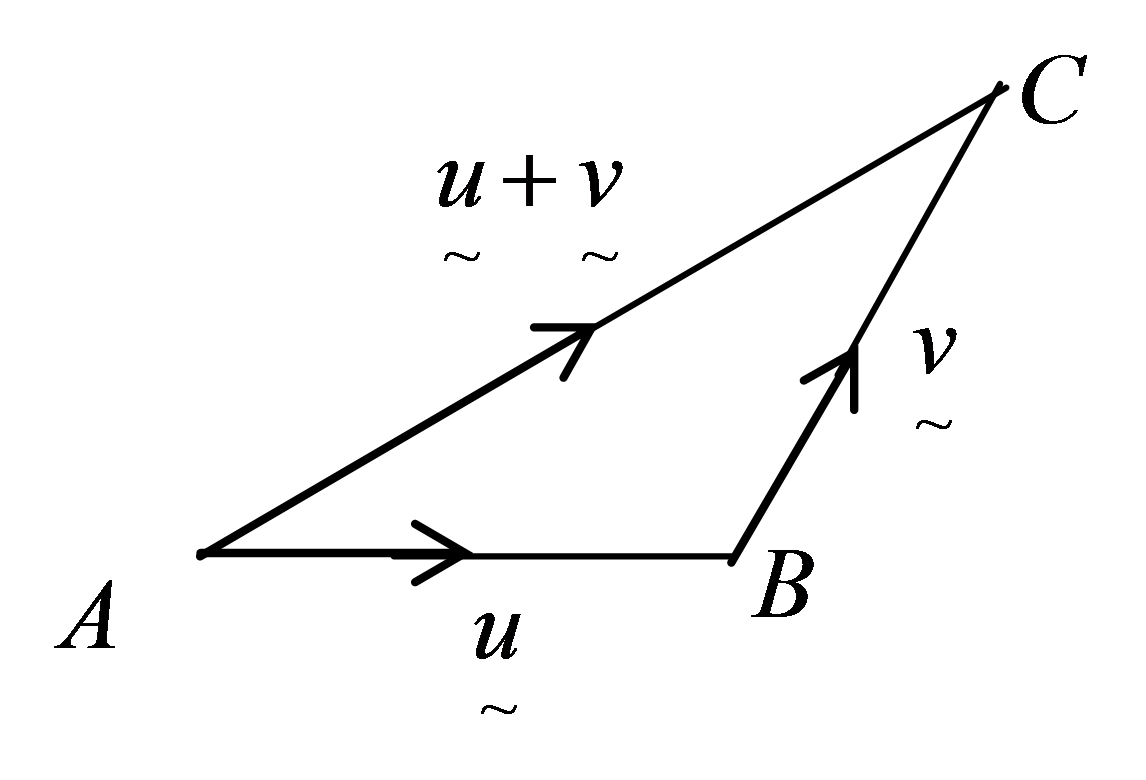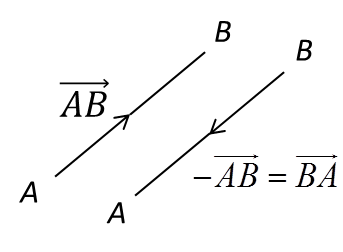Vectors In Cartesian Plane

Posted on April 22, 2020 by user

(A) Vectors in Cartesian Coordinates

1. A unit vector is a vector whose magnitude is one unit.

2. A unit vector that is parallel to the x-axis is denoted by

$\underset{˜}{i}$ while a unit vector that is parallel to the y-axis is denoted by

$\underset{˜}{j}$ .

3. The unit vector can be expressed in columnar form as below:

$\begin{array}{l} \vec{O A} = x \underset{˜}{i} + y \underset{˜}{j} \\ = (\begin{matrix} x \\ y \end{matrix}) \leftarrow (Column Vector) \end{array}$

4. The magnitudes of the unit vectors are

$| \underset{˜}{i} | = | \underset{˜}{j} | = 1.$

5. The magnitude of the vector

$\vec{O A}$ can be calculated using the Pythagoras’ Theorem.

$| \vec{O A} | = \sqrt{x^{2} + y^{2}}$

(B) Unit Vector in the Direction of a Vector

$Unit vector of \underset{˜}{a}, \underset{˜}{\hat{a}} = \frac{x \underset{˜}{i} + y \underset{˜}{j}}{\sqrt{x^{2} + y^{2}}}$

Example 1:

$\underset{˜}{r} = k \underset{˜}{i} - 8 \underset{˜}{j}$ and

$| \underset{˜}{r} | = 10$ , find the values of k. Determine the unit vector in the direction of

$\underset{˜}{r}$ for each value of k.

Solution:

$\begin{array}{l} \underset{˜}{r} = k \underset{˜}{i} - 8 \underset{˜}{j} \\ Given | \underset{˜}{r} | = 10 \\ \sqrt{x^{2} + y^{2}} = 10 \\ \sqrt{k^{2} + {(- 8)}^{2}} = 10 \\ k^{2} + 64 = 100 \\ k = \pm 6 \\ Unit vector of \hat{\underset{˜}{r}} = \frac{x \underset{˜}{i} + y \underset{˜}{j}}{\sqrt{x^{2} + y^{2}}} \\ When k = 6, When k = - 6 \\ \hat{\underset{˜}{r}} = \frac{6 \underset{˜}{i} - 8 \underset{˜}{j}}{10} = \frac{3 \underset{˜}{i} - 4 \underset{˜}{j}}{5}, \hat{\underset{˜}{r}} = \frac{- 6 \underset{˜}{i} - 8 \underset{˜}{j}}{10} = \frac{- 3 \underset{˜}{i} - 4 \underset{˜}{j}}{5} \\ \hat{\underset{˜}{r}} = \frac{1}{5} (3 \underset{˜}{i} - 4 \underset{˜}{j}), \hat{\underset{˜}{r}} = \frac{1}{5} (- 3 \underset{˜}{i} - 4 \underset{˜}{j}) \end{array}$

Example 2:

It is given that

$\underset{˜}{a} = (\begin{array}{l} 6 \\ 3 \end{array}) and \underset{˜}{b} = (\begin{array}{l} 3 \\ 7 \end{array}) .$

(a) Find

$\underset{˜}{b} - \underset{˜}{a} and | \underset{˜}{b} - \underset{˜}{a} | .$

(b) Hence, find the unit vector in the direction of

$\underset{˜}{b} - \underset{˜}{a} .$

Solution:

(a)

$\begin{array}{l} \underset{˜}{b} - \underset{˜}{a} = (\begin{array}{l} 3 \\ 7 \end{array}) - (\begin{array}{l} 6 \\ 3 \end{array}) = (\begin{array}{l} 3 - 6 \\ 7 - 3 \end{array}) = (\begin{array}{l} - 3 \\ 4 \end{array}) \\ | \underset{˜}{b} - \underset{˜}{a} | = \sqrt{{(- 3)}^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5 \end{array}$

(b)

$\begin{array}{l} The unit vector in the direction of \underset{˜}{b} - \underset{˜}{a} \\ = \frac{1}{5} (\begin{array}{l} - 3 \\ 4 \end{array}) \\ = (\begin{array}{l} - \frac{3}{5} \\ \frac{4}{5} \end{array}) \end{array}$

Short Question 1 – 3

Posted on April 22, 2020 by user

Question 1:
Given that O (0, 0), A (–3, 4) and B (–9, 12), find in terms of the unit vectors,

$\underset{˜}{i}$ and

$\underset{˜.}{j}$

(a)

$\vec{A B}$

(b) the unit vector in the direction of

$\vec{A B}$

Solution:
(a)

$\begin{array}{l} A = (- 3, 4), thus \vec{O A} = - 3 \underset{˜}{i} + 4 \underset{˜}{j} \\ B = (- 9, 12), thus \vec{O B} = - 9 \underset{˜}{i} + 12 \underset{˜}{j} \\ \vec{A B} = \vec{A O} + \vec{O B} \\ \vec{A B} = - (- 3 \underset{˜}{i} + 4 \underset{˜}{j}) + (- 9 \underset{˜}{i} + 12 \underset{˜}{j}) \\ \vec{A B} = 3 \underset{˜}{i} - 4 \underset{˜}{j} - 9 \underset{˜}{i} + 12 \underset{˜}{j} \\ \vec{A B} = - 6 \underset{˜}{i} + 8 \underset{˜}{j} \end{array}$

(b)

$\begin{array}{l} The magnitude of | \vec{A B} |, \\ | \vec{A B} | = \sqrt{{(- 6)}^{2} + {(8)}^{2}} = 10 \\ ∴ The unit vector in the direction of \vec{A B}, \\ \frac{\vec{A B}}{| \vec{A B} |} = \frac{1}{10} (- 6 \underset{˜}{i} + 8 \underset{˜}{j}) = - \frac{3}{5} \underset{˜}{i} + \frac{4}{5} \underset{˜}{j} \end{array}$

Question 2:
Given that A (–3, 2), B (4, 6) and C (m, n), find the value of m and of n such that

$2 \vec{A B} + \vec{B C} = (\begin{matrix} 12 \\ - 3 \end{matrix})$

Solution:

$\begin{array}{l} A = (\begin{array}{l} - 3 \\ 2 \end{array}), B = (\begin{array}{l} 4 \\ 6 \end{array}) and C = (\begin{array}{l} m \\ n \end{array}) \\ \vec{A B} = \vec{A O} + \vec{O B} \\ \vec{A B} = - (\begin{array}{l} - 3 \\ 2 \end{array}) + (\begin{array}{l} 4 \\ 6 \end{array}) = (\begin{array}{l} 7 \\ 4 \end{array}) \\ \vec{B C} = \vec{B O} + \vec{O C} \\ \vec{B C} = - (\begin{array}{l} 4 \\ 6 \end{array}) + (\begin{array}{l} m \\ n \end{array}) = (\begin{array}{l} - 4 + m \\ - 6 + n \end{array}) \\ Given 2 \vec{A B} + \vec{B C} = (\begin{matrix} 12 \\ - 3 \end{matrix}) \\ 2 (\begin{array}{l} 7 \\ 4 \end{array}) + (\begin{array}{l} - 4 + m \\ - 6 + n \end{array}) = (\begin{matrix} 12 \\ - 3 \end{matrix}) \\ (\begin{array}{l} 14 - 4 + m \\ 8 - 6 + n \end{array}) = (\begin{matrix} 12 \\ - 3 \end{matrix}) \\ 10 + m = 12 \\ m = 2 \\ 2 + n = - 3 \\ n = - 5 \end{array}$

Question 3:

Diagram below shows a rectangle OABC and the point D lies on the straight line OB.

It is given that OD = 3DB.

$Express \vec{O D} in terms of \underset{˜}{x} and \underset{˜}{y} .$

Solution:

$\begin{array}{l} \vec{O B} = \vec{O A} + \vec{A B} = 3 \underset{˜}{x} + 12 \underset{˜}{y} \\ \vec{O D} = 3 \vec{D B} \\ \frac{\vec{O D}}{\vec{D B}} = \frac{3}{1} \\ \vec{O D} : \vec{D B} = 3 : 1 \\ ∴ \vec{O D} = \frac{3}{4} \vec{O B} \\ = \frac{3}{4} (3 \underset{˜}{x} + 12 \underset{˜}{y}) \\ = \frac{9}{4} \underset{˜}{x} + 9 \underset{˜}{y} \end{array}$

4.3.1 Addition of Vectors

Posted on April 22, 2020 by user

4.3 Addition and Subtraction of Vectors

4.3.1 Addition of Vectors

1. The addition of two vectors,

$\underset{˜}{u} and \underset{˜}{v}$ , can be written as

$\underset{˜}{u} + \underset{˜}{v}$ . The result of this addition is a vector which is called the resultant vector.

2. When two vectors with the same direction is added up, the resultant vector has

(a) the same direction with both the vectors.

(b) a magnitude equal to the sum of the magnitudes of both the vectors.

Addition of Non-parallel Vectors

1. Addition of two non-parallel vectors,

$\underset{˜}{u} and \underset{˜}{v}$ , can be shown by using two laws.

(a) Triangle Law of Addition

The resultant vector

$\underset{˜}{u} + \underset{˜}{v}$ is represented by the third side AC.

(b) Parallelogram Law of Addition

The resultant vector

$\underset{˜}{u} + \underset{˜}{v}$ is represented by the third side AC.

4.1 Vector

Posted on April 22, 2020 by user

(A) Definition of Vector and Vector Notation

1. Vector is a quantity that has both magnitude and direction.

2. Scalar is a quantity that has magnitude only.

3. A vector can be presented by a line segment with an arrow, known as a directed line segment.

(B) Equality of Two Vectors

1. Negative vector of

$\vec{A B}$ has the same magnitude as

$\vec{A B}$ but its direction is opposite to that of

$\vec{A B}$ .

2. A zero vector is a vector whose magnitude is zero. It is denoted by

$\underset{˜}{0}$ .

3. Two vectors are equal if both the vectors have the same magnitude and direction.

Long Question 4

Posted on April 22, 2020 by user

Question 4:
Diagram below shows quadrilateral ABCD. The straight line AC intersects the straight line BD at point E.

$\begin{array}{l} It is given that B E : E D = 2 : 3, \vec{A B} = 10 \underset{˜}{x}, \vec{A D} = 25 \underset{˜}{y} and \vec{B C} = - \underset{˜}{x} + 15 \underset{˜}{y} . \\ (a) Express in terms of \underset{˜}{x} and \underset{˜}{y}, \\ (i) \vec{B D} \\ (ii) \vec{A E} \\ (b) Find the ratio A E : E C . \end{array}$

Solution:
(a)(i)

$\begin{array}{l} \vec{B D} = \vec{B A} + \vec{A D} \\ = \vec{A D} - \vec{A B} \\ = 25 \underset{˜}{y} - 10 \underset{˜}{x} \end{array}$

(a)(ii)

$\begin{array}{l} \vec{A E} = \vec{A B} + \vec{B E} \\ = \vec{A B} + \frac{2}{5} \vec{B D} \\ = 10 \underset{˜}{x} + \frac{2}{5} (25 \underset{˜}{y} - 10 \underset{˜}{x}) \\ = 10 \underset{˜}{x} + \frac{2}{5} (25 \underset{˜}{y} - 10 \underset{˜}{x}) \\ = 10 \underset{˜}{x} + 10 \underset{˜}{y} - 4 \underset{˜}{x} \\ = 6 \underset{˜}{x} + 10 \underset{˜}{y} \\ = 2 (3 \underset{˜}{x} + 5 \underset{˜}{y}) \end{array}$

(b)

$\begin{array}{l} \vec{E C} = \vec{E B} + \vec{B C} \\ = \vec{B C} - \vec{B E} \\ = \vec{B C} - \frac{2}{3} \vec{E D} \\ = \vec{B C} - \frac{2}{3} (\vec{E A} + \vec{A D}) \\ = - \underset{˜}{x} + 15 \underset{˜}{y} - \frac{2}{3} (- 6 \underset{˜}{x} - 10 \underset{˜}{y} + 25 \underset{˜}{y}) \\ = - \underset{˜}{x} + 15 \underset{˜}{y} - \frac{2}{3} (- 6 \underset{˜}{x} + 15 \underset{˜}{y}) \\ = - \underset{˜}{x} + 15 \underset{˜}{y} + 4 \underset{˜}{x} - 10 \underset{˜}{y} \\ = 3 \underset{˜}{x} + 5 \underset{˜}{y} \\ \frac{A E}{E C} = \frac{2 (3 \underset{˜}{x} + 5 \underset{˜}{y})}{1 (3 \underset{˜}{x} + 5 \underset{˜}{y})} \\ A E : E C = 2 : 1 \end{array}$

Long Question 1

Posted on April 22, 2020 by user

Question 1:

The above diagram shows triangle OAB. The straight line AP intersects the straight line OQ at R. It is given that

$O P = \frac{1}{4} O B, A Q = \frac{1}{4} A B, \vec{O P} = 4 \underset{˜}{b} and \vec{O A} = 8 \underset{˜}{a} .$

(a) Express in terms of

$\underset{˜}{a} and/ or \underset{˜}{b} :$

$\begin{array}{l} (i) \vec{A P} \\ (ii) \vec{O Q} \end{array}$

(b)(i) Given that

$\vec{A R} = h \vec{A P}$ , state

$\vec{A R}$ in terms of h,

$\underset{˜}{a} and \underset{˜}{b} .$
(ii) Given that

$\vec{R Q} = k \vec{O Q},$ state in terms of k,

$\underset{˜}{a} and \underset{˜}{b} .$

(c) Using

$\vec{A Q} = \vec{A R} + \vec{R Q},$ find the value of h and of k.

Solution:
(a)(i)

$\begin{array}{l} \vec{A P} = \vec{A O} + \vec{O P} \\ \vec{A P} = - \vec{O A} + \vec{O P} \\ \vec{A P} = - 8 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}$

(a)(ii)

$\begin{array}{l} \vec{O Q} = \vec{O A} + \vec{A Q} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} \vec{A B} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (\vec{A O} + \vec{O B}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 \vec{O P}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 (4 \underset{˜}{b})) \\ \vec{O Q} = 8 \underset{˜}{a} - 2 \underset{˜}{a} + 4 \underset{˜}{b} \\ \vec{O Q} = 6 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}$

(b)(i)

$\begin{array}{l} \vec{A R} = h \vec{A P} \\ \vec{A R} = h (- 8 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{A R} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} \end{array}$

(b)(ii)

$\begin{array}{l} \vec{R Q} = k \vec{O Q} \\ \vec{R Q} = k (6 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{R Q} = 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}$

(c)

$\begin{array}{l} \vec{A Q} = \vec{A R} + \vec{R Q} \\ \vec{A Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + (6 k \underset{˜}{a} + 4 k \underset{˜}{b}) \\ \vec{A O} + \vec{O Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 8 \underset{˜}{a} + 6 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 6 k \underset{˜}{a} + 4 h \underset{˜}{b} + 4 k \underset{˜}{b} \\ - 2 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 6 k \underset{˜}{a} + 4 h \underset{˜}{b} + 4 k \underset{˜}{b} \\ - 2 = - 8 h + 6 k \\ - 1 = - 4 h + 3 k \to (1) \\ 4 = 4 h + 4 k \\ 1 = h + k \\ k = 1 - h \to (2) \\ Substitute (2) into (1), \\ - 1 = - 4 h + 3 (1 - h) \\ - 1 = - 4 h + 3 - 3 h \\ - 4 = - 7 h \\ h = \frac{4}{7} \\ From (2), \\ k = 1 - \frac{4}{7} = \frac{3}{7} \end{array}$

Long Question 3

Posted on April 22, 2020 by user

Question 3:

In diagram below, PQRS is a quadrilateral. PTS and TUR are straight lines.

It is given that

$\vec{P Q} = 20 \underset{˜}{x}, \vec{P T} = 8 \underset{˜}{y}, \vec{S R} = 25 \underset{˜}{x} - 24 \underset{˜}{y}, \vec{P T} = \frac{1}{4} \vec{P S} and \vec{T U} = \frac{3}{5} \vec{T R}$

(a) Express in terms of

$\underset{˜}{x}$ and/or

$\underset{˜}{y}$ :

(i) $\vec{Q S}$
(ii) $\vec{T R}$
(b) Show that the points Q, U and S are collinear.

(c) If

$| \underset{˜}{x} |$ = 2 and

$| \underset{˜}{y} |$ = 3, find

$| \vec{Q S} |$

Solution:
(a)(i)

$\begin{array}{l} \vec{Q S} = \vec{Q P} + \vec{P S} \\ \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \leftarrow \begin{array}{l} Given \vec{P T} = \frac{1}{4} \vec{P S} \\ \vec{P S} = 4 \vec{P T} = 4 (8 \underset{˜}{y}) = 32 \underset{˜}{y} \end{array} \end{array}$

(a)(ii)

$\begin{array}{l} \vec{T R} = \vec{T S} + \vec{S R} \\ \vec{T R} = \frac{3}{4} \vec{P S} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = \frac{3}{4} (32 \underset{˜}{y}) + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 24 \underset{˜}{y} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 25 \underset{˜}{x} \end{array}$

(b)

$\begin{array}{l} \vec{Q U} = \vec{Q P} + \vec{P T} + \vec{T U} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + \frac{3}{5} (25 \underset{˜}{x}) \leftarrow \begin{array}{l} Given \\ \vec{T U} = \frac{3}{5} \vec{T R} \end{array} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + 15 \underset{˜}{x} \\ \vec{Q U} = - 5 \underset{˜}{x} + 8 \underset{˜}{y} \\ From (a)(i) \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{- 20 \underset{˜}{x} + 32 \underset{˜}{y}}{- 5 \underset{˜}{x} + 8 \underset{˜}{y}} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{4 (- 5 \underset{˜}{x} + 8 \underset{˜}{y})}{(- 5 \underset{˜}{x} + 8 \underset{˜}{y})} \\ \frac{\vec{Q S}}{\vec{Q U}} = 4 \\ \vec{Q S} = 4 \vec{Q U} \\ ∴ Q, U and S are collinear . \end{array}$

(c)

$\begin{array}{l} \vec{P S} = 32 \underset{˜}{y} \\ | \vec{P S} | = 32 | \underset{˜}{y} | \\ | \vec{P S} | = 32 \times 3 = 96 \\ \vec{P Q} = 20 \underset{˜}{x} \\ | \vec{P Q} | = 20 | \underset{˜}{x} | \\ | \vec{P Q} | = 20 \times 2 = 40 \\ ∴ | \vec{Q S} | = \sqrt{96^{2} + 40^{2}} \\ | \vec{Q S} | = 104 \end{array}$

4.4 Expression of a Vector as the Linear Combination of a Few Vectors

Posted on April 22, 2020 by user

4.4 Expression of a Vector as the Linear Combination of a Few Vectors

1. Polygon Law for Vectors

$\vec{P Q} = \vec{P U} + \vec{U T} + \vec{T S} + \vec{S R} + \vec{R Q}$

2. To prove that two vectors are parallel, we must express one of the vectors as a scalar multiple of the other vector.

For example,

$\vec{A B} = k \vec{C D} or \vec{C D} = h \vec{A B} .$ .

3. To prove that points P, Q and R are collinear, prove one of the following.

$\begin{array}{l} • \vec{P Q} = k \vec{Q R} or \vec{Q R} = h \vec{P Q} \\ • \vec{P R} = k \vec{P Q} or \vec{P Q} = h \vec{P R} \\ • \vec{P R} = k \vec{Q R} or \vec{Q R} = h \vec{P R} \end{array}$

Example:

Diagram below shows a parallelogram ABCD. Point Q lies on the straight line AB and point S lies on the straight line DC. The straight line AS is extended to the point T such that AS = 2ST.

It is given that AQ : QB = 3 : 1, DS : SC = 3 : 1,

$\vec{A Q} = 6 \underset{˜}{a} and \vec{A D} = \underset{˜}{b}$

(a) Express, in terms of

$\underset{˜}{a} and \underset{˜}{b} :$

$(i) \vec{A S} (ii) \vec{Q C}$
(b) Show that the points Q, C and T are collinear.

Solution:

$\begin{array}{l} (a)(i) \vec{A S} = \vec{A D} + \vec{D S} \\ = \vec{A D} + \vec{A Q} \leftarrow \begin{array}{l} A Q : Q B = 3 : 1 and \\ D S : S C = 3 : 1 \\ ∴ \vec{A Q} = \vec{D S} \end{array} \\ = \underset{˜}{b} + 6 \underset{˜}{a} \\ = 6 \underset{˜}{a} + \underset{˜}{b} \end{array}$

$\begin{array}{l} (a)(ii) \vec{Q C} = \vec{Q B} + \vec{B C} \\ = \frac{1}{3} \vec{A Q} + \vec{A D} \leftarrow \begin{array}{l} A Q : Q B = 3 : 1 \\ \frac{A Q}{Q B} = \frac{3}{1} \Rightarrow Q B = \frac{1}{3} A Q \\ and for parallelogram, \\ B C / / A D, B C = A D \end{array} \\ = \frac{1}{3} (6 \underset{˜}{a}) + \underset{˜}{b} \\ = 2 \underset{˜}{a} + \underset{˜}{b} \end{array}$

$\begin{array}{l} (b) \vec{Q T} = \vec{Q A} + \vec{A T} \\ = \vec{Q A} + \frac{3}{2} \vec{A S} \leftarrow \begin{array}{l} A S = 2 S T \\ A T = 3 S T = \frac{3}{2} A S \end{array} \\ = - 6 \underset{˜}{a} + \frac{3}{2} (6 \underset{˜}{a} + \underset{˜}{b}) \\ = 3 \underset{˜}{a} + \frac{3}{2} \underset{˜}{b} \\ = \frac{3}{2} (2 \underset{˜}{a} + \underset{˜}{b}) \\ = \frac{3}{2} \vec{Q C} \\ ∴ Points Q, C and T are collinear . \end{array}$

Integration as the Inverse of Differentiation

Posted on April 22, 2020 by user

3.4c Integration as the Inverse of Differentiation

Example:

$\begin{array}{l} Shows that \frac{d}{d x} [\frac{2 x + 5}{x^{2} - 3}] = \frac{- 2 (x^{2} + 5 x + 3)}{{(x^{2} - 3)}^{2}} \\ Hence, find the value of \int_{0}^{2} \frac{(x^{2} + 5 x + 3)}{{(x^{2} - 3)}^{2}} d x \end{array}$

Solution:

$\begin{array}{l} \frac{d}{d x} [\frac{2 x + 5}{x^{2} - 3}] = \frac{(x^{2} - 3) (2) - (2 x + 5) (2 x)}{{(x^{2} - 3)}^{2}} \\ = \frac{2 x^{2} - 6 - 4 x^{2} - 10 x}{{(x^{2} - 3)}^{2}} \\ = \frac{- 2 x^{2} - 10 x - 6}{{(x^{2} - 3)}^{2}} \\ = \frac{- 2 (x^{2} + 5 x + 3)}{{(x^{2} - 3)}^{2}} \\ \int_{0}^{2} \frac{- 2 (x^{2} + 5 x + 3)}{{(x^{2} - 3)}^{2}} d x = {[\frac{2 x + 5}{x^{2} - 3}]}_{0}^{2} \\ - 2 \int_{0}^{2} \frac{(x^{2} + 5 x + 3)}{{(x^{2} - 3)}^{2}} d x = {[\frac{2 x + 5}{x^{2} - 3}]}_{0}^{2} \\ \int_{0}^{2} \frac{(x^{2} + 5 x + 3)}{{(x^{2} - 3)}^{2}} d x = - \frac{1}{2} [(\frac{2 (2) + 5}{2^{2} - 3}) - (\frac{2 (0) + 5}{0^{2} - 3})] \\ = - \frac{1}{2} [9 - (- \frac{5}{3})] \\ = - \frac{1}{2} \times \frac{32}{3} \\ = - \frac{16}{3} \\ = - 5 \frac{1}{3} \end{array}$

3.6 Integration as the Summation of Volumes

Posted on April 22, 2020 by user

3.6 Integration as the Summation of Volumes

(1).

The volume of the solid generated when the region enclosed by the curve y = f(x), the x-axis, the line x = a and the line x = b is revolved through 360° about the x-axis is given by

$V_{x} = π \int_{a}^{b} y^{2} d x$

(2).

The volume of the solid generated when the region enclosed by the curve x = f(y), the y-axis, the line y = a and the line y = b is revolved through 360° about the y-axis is given by

$V_{y} = π \int_{a}^{b} x^{2} d y$