Question 1:
Table below shows the price indices and percentage of usage of four items, P , Q , R and S , which are the main ingredients in the production of a type of toy.
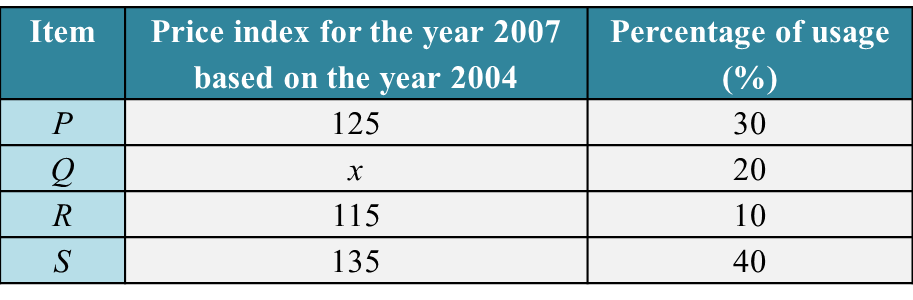
(a) Calculate
(i) the price of S in the year 2004 if its price in the year 2007 is RM43.20 ,
(ii) the price index of P in the year 2007 based on the year 2002 if its price index in the year 2004 based on the year 2002 is 110.
(b) The composite index of the cost of toy production for the year 2007 based on the year 2004 is 125.
Calculate
(i) the value of x ,
(ii) the price of the toy in the year 2004 if the corresponding price in the year 2007 is RM75.
135=43.2P2004×100P2004=43.2×100135=32∴
(a)(ii)
(b)(i)
(b)(ii)
Table below shows the price indices and percentage of usage of four items, P , Q , R and S , which are the main ingredients in the production of a type of toy.

(a) Calculate
(i) the price of S in the year 2004 if its price in the year 2007 is RM43.20 ,
(ii) the price index of P in the year 2007 based on the year 2002 if its price index in the year 2004 based on the year 2002 is 110.
(b) The composite index of the cost of toy production for the year 2007 based on the year 2004 is 125.
Calculate
(i) the value of x ,
(ii) the price of the toy in the year 2004 if the corresponding price in the year 2007 is RM75.
Solution:
(a)(i)135=43.2P2004×100P2004=43.2×100135=32∴
(a)(ii)
(b)(i)
(b)(ii)


 (a) Calculate
(a) Calculate