9.9 Small Changes and Approximations

Posted on April 22, 2020 by user

[adinserter block="3"]

9.9 Small Changes and Approximations

$If δ x is very small, \frac{δ y}{δ x} will be a good approximation of \frac{d y}{d x},$ ,

This is very useful information in determining an approximation of the change in one variable given the small change in the second variable.

[adinserter block="3"]

Example:

Given that y = 3x² + 2x – 4. Use differentiation to find the small change in y when x increases from 2 to 2.02.

Solution:

$\begin{array}{l} y = 3 x^{2} + 2 x - 4 \\ \frac{d y}{d x} = 6 x + 2 \end{array}$

The small change in y is denoted by δy while the small change in the second quantity that can be seen in the question is the x and is denoted by δx.

$\begin{array}{l} \frac{δ y}{δ x} \approx \frac{d y}{d x} \\ δ y = \frac{d y}{d x} \times δ x \\ δ y = (6 x + 2) \times (2.02 - 2) \to δ x = new x - original x \\ δ y = [6 (2) + 2] \times 0.02 \\ Substitute x with the original value of x, i .e . 2. \\ δ y = 0.28 \end{array}$

Related Rates of Change

Posted on April 22, 2020 by user

(A) Related Rates of Change

1. If two variables x and y are connected by the equation y = f(x)

Notes:

If x changes at the rate of 5 cms ^-1⇒

$\frac{d x}{d t} = 5$

Decreases/leaks/reduces Þ NEGATIVES values!!!

Example 1 (Rate of change of y and x)

Two variables, x and y are related by the equation

$y = 4 x + \frac{3}{x}$ . Given that y increases at a constant rate of 2 units per second, find the rate of change of x when x = 3.

Solution:

$\begin{array}{l} y = 4 x + \frac{3}{x} = 4 x + 3 x^{- 1} \\ \frac{d y}{d x} = 4 - 3 x^{- 2} = 4 - \frac{3}{x^{2}} \\ \frac{d y}{d t} = \frac{d y}{d x} \times \frac{d x}{d t} \\ 2 = (4 - \frac{3}{x^{2}}) \times \frac{d x}{d t} \\ when x = 3 \\ 2 = (4 - \frac{3}{3^{2}}) \times \frac{d x}{d t} \\ 2 = \frac{11}{3} \times \frac{d x}{d t} \\ \frac{d x}{d t} = \frac{6}{11} unit s^{- 1} \end{array}$

(B) Rates of Change of Volume, Area, Radius, Height and Length

(C) Rate of Change of Any Combination of Two Variables

9.7 Second-Order Differentiation, Turning Points, Maximum and Minimum Points

Posted on April 22, 2020 by user

(A) Second-Order Differentiation

1. When a function y = x³+ x²– 3x + 6 is differentiated with respect to x, the derivative

$\frac{d y}{d x} = 3 x^{2} + 2 x - 3$

2. The second function

$\frac{d y}{d x}$ can be differentiated again with respect to x. This is called the second derivative of y with respect to x and can be written as

$\frac{d^{2} y}{d x^{2}}$ .

3. Take note that

$\frac{d^{2} y}{d x^{2}} \neq {(\frac{d y}{d x})}^{2}$ .

For example,

If y = 4x³ – 7x² + 5x – 1,

The first derivative

$\frac{d y}{d x} = 12 x^{2} - 14 x + 5$

The second derivative

$\frac{d^{2} y}{d x^{2}} = 24 x - 14$

(B) Turning Points, Maximum and Minimum Points

(a) At Turning Points A and B,

(b) At Maximum Point A,

(c) At Minimum Point B,

9.6 Gradients of Tangents, Equations of Tangent and Normal

Posted on April 22, 2020 by user

9.6 Gradients of Tangents, Equations of Tangents and Normals

If A(x₁, y₁) is a point on a line y = f(x), the gradient of the line (for a straight line) or the gradient of the tangent of the line (for a curve) is the value of

$\frac{d y}{d x}$ when x = x₁.

(A) Gradient of tangent at A(x₁, y₁):

(B) Equation of tangent:

(C) Gradient of normal at A(x₁, y₁):

(D) Equation of normal :

Example 1 (Find the Equation of Tangent)

Given that

$y = \frac{4}{{(3 x - 1)}^{2}}$ . Find the equation of the tangent at the point (1, 1).

Solution:

$\begin{array}{l} y = \frac{4}{{(3 x - 1)}^{2}} = 4 {(3 x - 1)}^{- 2} \\ \frac{d y}{d x} = - 2.4 {(3 x - 1)}^{- 3} .3 \\ \frac{d y}{d x} = \frac{- 24}{{(3 x - 1)}^{3}} \\ At point (1, 1), \frac{d y}{d x} = \frac{- 24}{{[3 (1) - 1]}^{3}} = \frac{- 24}{8} = - 3 \\ Equation of tangent at point (1, 1) is, \\ y - 1 = - 3 (x - 1) \\ y - 1 = - 3 x + 3 \\ y = - 3 x + 4 \end{array}$

Example 2 (Find the Equation of Normal)

Find the gradient of the curve

$y = \frac{7}{3 x + 4}$ at the point (-1, 7). Hence, find the equation of the normal to the curve at this point.

Solution:

$\begin{array}{l} y = \frac{7}{3 x + 4} = 7 {(3 x + 4)}^{- 1} \\ \frac{d y}{d x} = - 7 {(3 x + 4)}^{- 2} .3 \\ \frac{d y}{d x} = \frac{- 21}{{(3 x + 4)}^{2}} \\ At point (- 1, 7), \frac{d y}{d x} = \frac{- 21}{{[3 (- 1) + 4]}^{2}} = - 21 \\ Gradient of the normal = \frac{1}{21} \\ Equation of the normal is \\ y - y_{1} = m (x - x_{1}) \\ y - 7 = \frac{1}{21} (x - (- 1)) \\ 21 y - 147 = x + 1 \\ 21 y - x - 148 = 0 \end{array}$

9.5 First Derivatives of Composite Function

Posted on April 22, 2020 by user

(A) Differentiate Composite Function using Chain Rule

Example:

Differentiate y = (x²– 1)⁸ .

Solution:

(B) Differentiate Composite Function using Alternative Method
- Easy Version

Example:

Differentiate y = (x² – 1)⁸ .

Solution:

$\begin{array}{l} y = {(x^{2} - 1)}^{8} \\ \frac{d y}{d x} = 8 {(x^{2} - 1)}^{7} \frac{d}{d x} (x^{2} - 1) \\ \frac{d y}{d x} = 8 {(x^{2} - 1)}^{7} (2 x) \\ \frac{d y}{d x} = 16 x {(x^{2} - 1)}^{7} \end{array}$

Practice 1:

$Given that y = \frac{1}{3 x - 7}, find \frac{d y}{d x}$

Solution:

$\begin{array}{l} y = \frac{1}{3 x - 7} = {(3 x - 7)}^{- 1} \\ \frac{d y}{d x} = - 1 {(3 x - 7)}^{- 2} .3 \\ \frac{d y}{d x} = \frac{- 3}{{(3 x - 7)}^{2}} \end{array}$

Practice 2:

$Given that y = \sqrt{2 x^{2} - 5 x + 1}, find \frac{d y}{d x}$

Solution:

$\begin{array}{l} y = \sqrt{2 x^{2} - 5 x + 1} = {(2 x^{2} - 5 x + 1)}^{\frac{1}{2}} \\ \frac{d y}{d x} = \frac{1}{2} {(2 x^{2} - 5 x + 1)}^{- \frac{1}{2}} (4 x - 5) \\ \frac{d y}{d x} = \frac{4 x - 5}{2 \sqrt{2 x^{2} - 5 x + 1}} \end{array}$

9.4 First Derivatives of the Quotient of Two Polynomials

Posted on April 22, 2020 by user

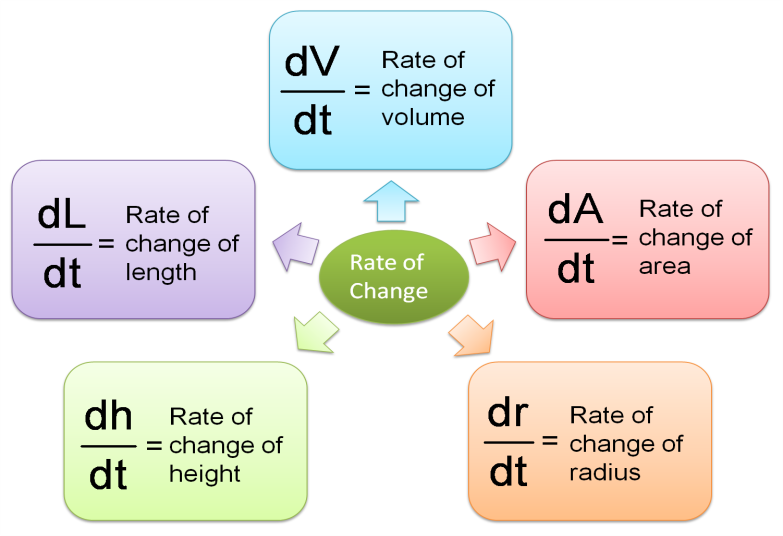
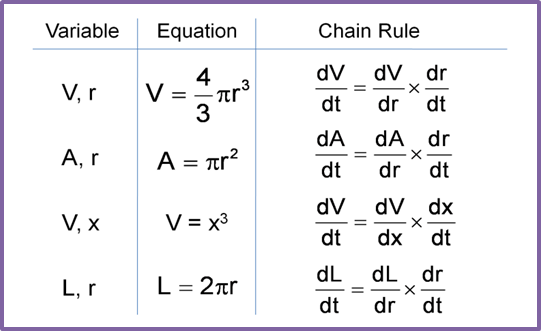
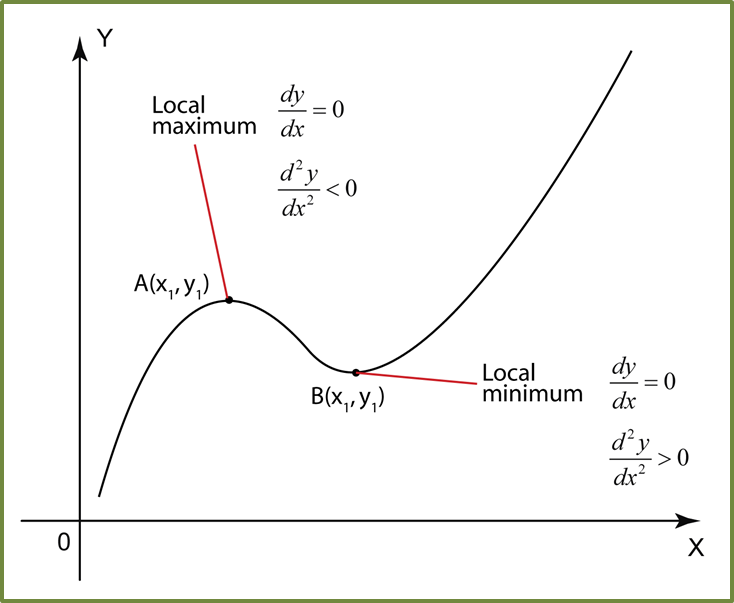
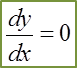
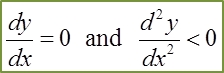
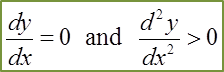
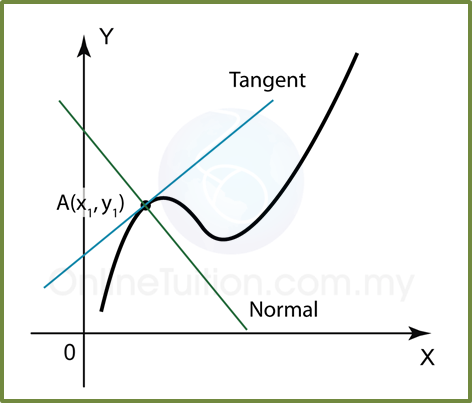
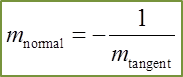
Find the Derivatives of a Quotient using Quotient Rule

Method 1: The Quotient Rule

Example:

Method 2: (Differentiate Directly)

Example:

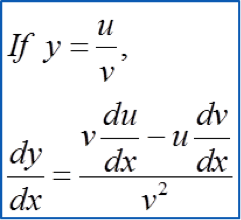
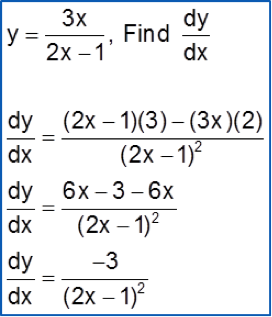
$Given that y = \frac{x^{2}}{2 x + 1}, find \frac{d y}{d x}$

Solution:

$\begin{array}{l} y = \frac{x^{2}}{2 x + 1} \\ \frac{d y}{d x} = \frac{(2 x + 1) (2 x) - x^{2} (2)}{{(2 x + 1)}^{2}} \\ = \frac{4 x^{2} + 2 x - 2 x^{2}}{{(2 x + 1)}^{2}} = \frac{2 x^{2} + 2 x}{{(2 x + 1)}^{2}} \end{array}$

Practice 1:

$Given that y = \frac{4 x^{3}}{{(5 x + 1)}^{3}}, find \frac{d y}{d x}$

Solution:

$\begin{array}{l} y = \frac{4 x^{3}}{{(5 x + 1)}^{3}} \\ \frac{d y}{d x} = \frac{{(5 x + 1)}^{3} (12 x^{2}) - 4 x^{3} .3 {(5 x + 1)}^{2} .5}{{[{(5 x + 1)}^{3}]}^{2}} \\ = \frac{{(5 x + 1)}^{3} (12 x^{2}) - 60 x^{3} {(5 x + 1)}^{2}}{{(5 x + 1)}^{6}} \\ = \frac{(12 x^{2}) {(5 x + 1)}^{2} [(5 x + 1) - 5 x]}{{(5 x + 1)}^{6}} \\ = \frac{(12 x^{2}) {(5 x + 1)}^{2} (1)}{{(5 x + 1)}^{6}} \\ = \frac{12 x^{2}}{{(5 x + 1)}^{4}} \end{array}$

9.4 First Derivatives of the Quotient of Two Polynomials

Posted on April 22, 2020 by user

9.4 Find the Derivatives of a Quotient using Quotient Rule

Method 1

The Quotient Rule

Example:

Method 2 (Differentiate Directly)

Example:

$Given that y = \frac{x^{2}}{2 x + 1}, find \frac{d y}{d x}$

Solution:

Practice 1:

$Given that y = \frac{4 x^{3}}{{(5 x + 1)}^{3}}, find \frac{d y}{d x}$

Solution:

9.2 First Derivative for Polynomial Function

Posted on April 22, 2020 by user

9.2 First Derivative for Polynomial Function

(A) Differentiating a Constant

(B) Differentiating Variable with Index n

(C) Differentiating a Linear Function

(D) Differentiating a Polynomial Function

(E) Differentiating Fractional Function

(F) Differentiating Square Root Function

Long Questions (Question 4)

Posted on April 21, 2020 by user

Question 4:

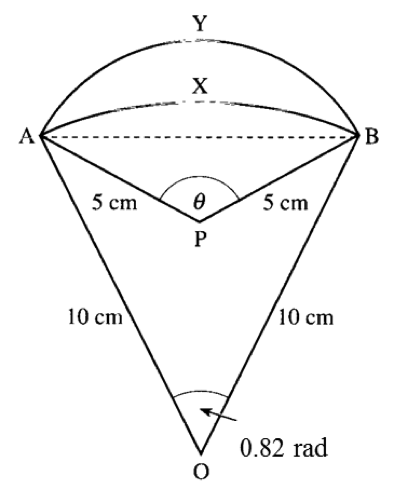
In the diagram above, AXB is an arc of a circle centre O and radius 10 cm with ∠AOB = 0.82 radian. AYB is an arc of a circle centre P and radius 5 cm with ∠APB = θ. Calculate:

the length of the chord AB,
the value of θ in radians,
the difference in length between the arcs AYB and AXB.

Solution:

(a)
$\begin{array}{l} \frac{1}{2} A B = \sin 0.41 \times 10 \to (Change the calculator to Rad mode) \\ \frac{1}{2} A B = 3.99 \\ ∴ The length of chord A B = 3.99 \times 2 = 7.98 c m . \end{array}$

(b)
$\begin{array}{l} Let \frac{1}{2} θ = α, θ = 2 α \\ \sin α = \frac{3.99}{5} \\ α = 0.924 rad \\ ∴ θ = 0.924 \times 2 = 1.848 radian . \end{array}$

(c)
Using s = rθ
Arcs AXB = 10 × 0.82 = 8.2 cm
Arcs AYB = 5 × 1.848 = 9.24 cm

Difference in length between the arcs AYB and AXB
= 9.24 – 8.2
= 1.04 cm

Long Questions (Question 3)

Posted on April 21, 2020 by user

Question 3:
Diagram below shows a sector QPR with centre P and sector POQ, with centre O.

It is given that OP = 17 cm and PQ = 8.8 cm.
[Use π = 3.142]
Calculate
(a) angle OPQ, in radians,
(b) the perimeter, in cm, of sector QPR,
(c) the area, in cm², of the shaded region.

Solution:

$\begin{array}{l} (a) \\ ∠ O P Q = ∠ O Q P \\ x + x + 30 = 180 \\ 2 x = 150 \\ x = 75 \\ ∠ O P Q = \frac{75 \times 3.142}{180} \\ = 1.3092 radians \end{array}$

$\begin{array}{l} (b) \\ Length of arc Q R = r θ \\ = 8.8 \times 1.3092 \\ = 11.52 cm \\ Perimeter of sector Q P R \\ = 11.52 + 8.8 + 8.8 \\ = 29.12 cm \end{array}$

$\begin{array}{l} (c) \\ 30^{o} = \frac{30 \times 3.142}{180} = 0.5237 rad \\ Area of segment P Q \\ = \frac{1}{2} r^{2} (θ - \sin θ) \\ = \frac{1}{2} \times 17^{2} \times (0.5237 - \sin 30) \\ = \frac{1}{2} \times 289 \times (0.5237 - 0.5) \\ = 3.4247 {cm}^{2} \\ Area of sector Q P R \\ = \frac{1}{2} r^{2} θ \\ = \frac{1}{2} \times {8.8}^{2} \times 1.3092 \\ = 50.692 {cm}^{2} \\ Area of shaded region \\ = 3.4247 + 50.692 \\ = 54.1167 {cm}^{2} \end{array}$