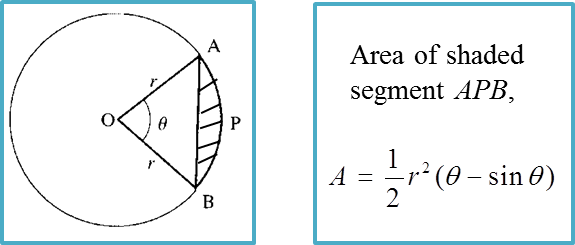
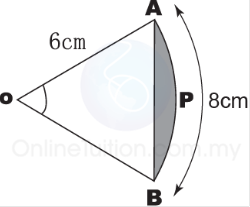
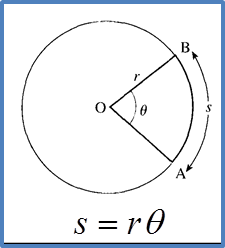
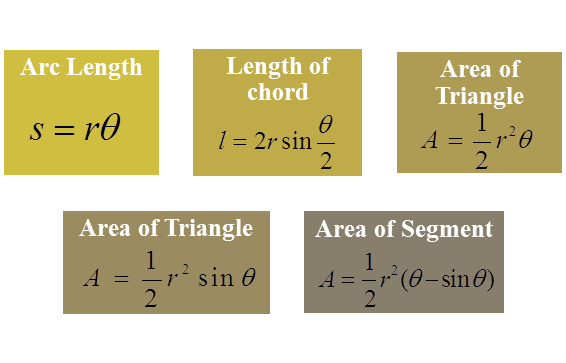Question 2:
Diagram below shows a semicircle PTQ, with centre O and quadrant of a circle RST, with centre R.
 [Use π = 3.142]
[Use π = 3.142]
Calculate
(a) the value of θ, in radians,
(b) the perimeter, in cm, of the whole diagram,
(c) the area, in cm2, of the shaded region.
Solution:
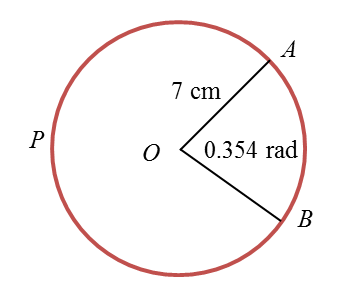
(a)sin∠ROT=2.55 ∠ROT=30oθ=180o−30o=150o =150×π180 =2.618 rad
(b)Length of arc PT=rθ =5×2.618 =13.09 cmLength of arc ST=π2×2.5 =3.9275 cmOR2+2.52=52 OR2=52−2.52OR=4.330Perimeter=13.09+3.9275+2.5+4.330+5 =28.8475 cm
(c)Area of shaded region=Area of quadrant RST−Area of quadrant RQTArea of quadrant RQT=Area of OQT−Area of OTR=12(5)2×(30×π180)−12(4.33)(2.5)=1.1333 cm2Area of shaded region=Area of quadrant RST−Area of quadrant RQT=12(2.5)2×(90×π180)−1.1333=3.7661 cm2
Diagram below shows a semicircle PTQ, with centre O and quadrant of a circle RST, with centre R.
 [Use π = 3.142]
[Use π = 3.142]Calculate
(a) the value of θ, in radians,
(b) the perimeter, in cm, of the whole diagram,
(c) the area, in cm2, of the shaded region.
Solution:
(a)sin∠ROT=2.55 ∠ROT=30oθ=180o−30o=150o =150×π180 =2.618 rad
(b)Length of arc PT=rθ =5×2.618 =13.09 cmLength of arc ST=π2×2.5 =3.9275 cmOR2+2.52=52 OR2=52−2.52OR=4.330Perimeter=13.09+3.9275+2.5+4.330+5 =28.8475 cm
(c)Area of shaded region=Area of quadrant RST−Area of quadrant RQTArea of quadrant RQT=Area of OQT−Area of OTR=12(5)2×(30×π180)−12(4.33)(2.5)=1.1333 cm2Area of shaded region=Area of quadrant RST−Area of quadrant RQT=12(2.5)2×(90×π180)−1.1333=3.7661 cm2
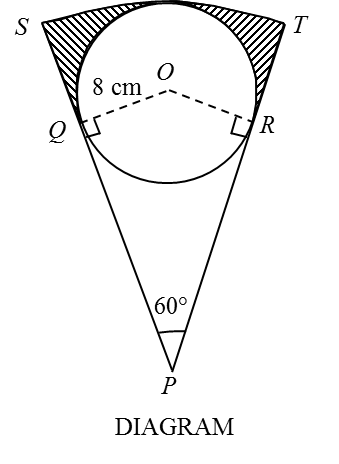
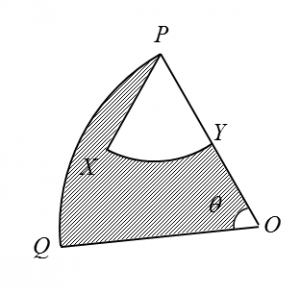 Given that OQ = 8 cm, PY = 3 cm ,
Given that OQ = 8 cm, PY = 3 cm ,