7.1a Mean

Posted on April 21, 2020 by user

7.1a Mean
1. The mean of the data is an average value obtained by using the formula:
Mean= Total data values Number of data

(A) Ungrouped Data

Example 1

(a) Find the mean for the set of data 2, 4, 7, 10, 13, 16 and 18.

(b) A value of xis added into the above set of data, the mean for this new data is 9.5. Determine the value of x.

Solution:
(a)

\begin{array}{l} \bar{x} = \frac{2 + 4 + 7 + 10 + 13 + 16 + 18}{7} \\ \bar{x} = \frac{70}{7} = 10 \end{array}

(b)

\begin{array}{l} New mean = 9.5 \\ \frac{70 + x}{8} = 9.5 \\ 70 + x = 76 \\ x = 6 \end{array}

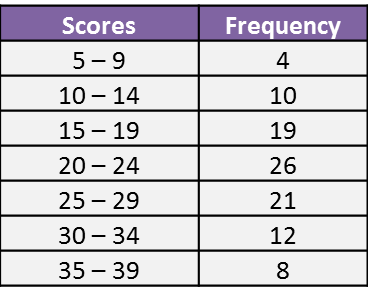
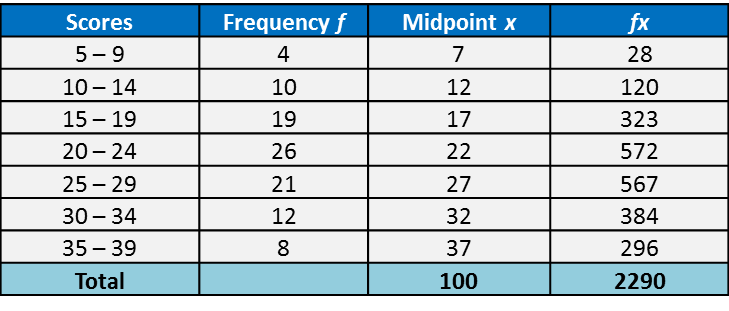
(B) Grouped Data (Without Class Interval)

Example 2

The frequency table shows the marks obtained by 40 students in a Biology test.

Find the mean marks.

Solution:

\begin{array}{l} Mean marks, \bar{x} \\ \bar{x} = \frac{(50) (6) + (55) (8) + (60) (15) + (65) (10) + (70) (1)}{6 + 8 + 15 + 10 + 1} \\ \bar{x} = \frac{2360}{40} = 59 \end{array}

(C) Grouped Data (With Class Interval)

Example 3

The grouped frequency distribution was obtained from 100 students regarding the scores in their test shown as below.

Find the mean scores.

Solution:

\begin{array}{l} Mid-point = \frac{5 + 9}{2} = 7 \\ Mean scores, \bar{x} = \frac{\sum f x}{\sum f} = \frac{2290}{100} = 22.9 \end{array}

Long Questions (Question 4)

Posted on April 21, 2020 by user

Question 4:
Solutions by scale drawing will not be accepted.
Diagram below shows a triangle PRS. Side PR intersects the y-axis at point Q.

(a) Given PQ : QR = 2 : 3, find
(i) The coordinates of P,
(ii) The equation of the straight line PS,
(iii) The area, in unit², of triangle PRS.
(b) Point M moves such that its distance from point R is always twice its distance from point S.
Find the equation of the locus M.

Solution:
(a)(i)

\begin{array}{l} P = (\frac{2 (6) + 3 h}{2 + 3}, \frac{2 (12) + 3 k}{2 + 3}) \\ (0, 6) = (\frac{12 + 3 h}{5}, \frac{24 + 3 k}{5}) \\ \frac{12 + 3 h}{5} = 0 \\ 3 h = - 12 \\ h = - 4 \\ \frac{24 + 3 k}{5} = 6 \\ 3 k = 30 - 24 \\ k = 2 \\ P = (- 4, 2) \end{array}

(a)(ii)

\begin{array}{l} m_{P S} = \frac{2 - (- 6)}{- 4 - 2} \\ = - \frac{8}{6} \\ = - \frac{4}{3} \\ Equation of P S : \\ y - y_{1} = - \frac{4}{3} (x - 2) \\ y - (- 6) = - \frac{4}{3} x + \frac{8}{3} \\ 3 y + 18 = - 4 x + 8 \\ 3 y = - 4 x - 10 \end{array}

(a)(iii)

\begin{array}{l} Area of △ P R S \\ = \frac{1}{2} | \begin{array}{l} - 4      2       6 \\ 2 - 612 \end{array} \begin{array}{l} - 4 \\ 2 \end{array} | \\ = \frac{1}{2} | (24 + 24 + 12) - (4 - 36 - 48) | \\ = \frac{1}{2} | 60 - (- 80) | \\ = 70 {unit}^{2} \end{array}

(b)

\begin{array}{l} Let P = (x, y) \\ M R = 2 M S \\ \sqrt{{(x - 6)}^{2} + {(y - 12)}^{2}} = 2 \sqrt{{(x - 2)}^{2} + {(y + 6)}^{2}} \\ {(x - 6)}^{2} + {(y - 12)}^{2} = 4 [{(x - 2)}^{2} + {(y + 6)}^{2}] \\ x^{2} - 12 x + 36 + y^{2} - 24 y + 144 = 4 [x^{2} - 4 x + 4 + y^{2} + 12 y + 36] \\ x^{2} - 12 x + y^{2} - 24 y + 180 = 4 x^{2} - 16 x + 4 y^{2} + 48 y + 160 \\ 3 x^{2} + 3 y^{2} - 4 x + 72 y - 20 = 0 \end{array}

Long Questions (Question 3)

Posted on April 21, 2020 by user

Question 3:

The diagram shows a triangle LMN where L is on the y-axis. The equation of the straight line LKN and MK are 2y – 3x + 6 = 0 and 3y + x– 13 = 0 respectively. Find

(a) the coordinates of K

(b) the ratio LK:KN

Solution:
(a)

2y – 3x + 6 = 0 ----(1)

3y + x – 13 = 0 ----(2)

x = 13 – 3y ----(3)

Substitute equation (3) into (1),

2y – 3 (13 – 3y) + 6 = 0

2y – 39 + 9y + 6 = 0

11y = 33

y = 3

Substitute y = 3 into equation (3),

x = 13 – 3 (3)

x = 4

Coordinates of K = (4, 3).

(b)

Given equation of LKN is 2y – 3x + 6 = 0

At y – axis, x = 0,

x coordinates of point L = 0.

\begin{array}{l} Ratio L K : K N \\ Equating the x coordinates, \\ \frac{L K (10) + K N (0)}{L K + K N} = 4 \\ 10 L K = 4 L K + 4 K N \\ 6 L K = 4 K N \\ \frac{L K}{K N} = \frac{4}{6} \\ \frac{L K}{K N} = \frac{2}{3} \\ Ratio L K : K N = 2 : 3 \end{array}

Long Questions (Question 2)

Posted on April 21, 2020 by user

Question 2:

In the diagram, PRS and QRT are straight lines. Given R is the midpoint of PS and
QR : RT = 1 : 3, Find

(a) the coordinates of R,

(b) the coordinates of T,

(c) the coordinates of the point of intersection between lines PQ and ST produced.

Solution:
(a)

Given R is the midpoint of PS.

\begin{array}{l} R = (\frac{3 + 7}{2}, \frac{2 + 6}{2}) \\ R = (5, 4) \end{array}

(b)

\begin{array}{l} Q R : R T = 1 : 3 \\ Lets coordinates of T = (x, y) \\ (\frac{(1) (x) + (3) (4)}{1 + 3}, \frac{(1) (y) + (3) (5)}{1 + 3}) = (5, 4) \\ \frac{x + 12}{4} = 5 \\ x + 12 = 20 \\ x = 8 \\ \frac{y + 15}{4} = 4 \\ y + 15 = 16 \\ y = 1 \\ T = (8, 1) \end{array}

(c)

\begin{array}{l} Gradient of P Q = \frac{5 - 2}{4 - 3} = 3 \\ Equation of P Q, \\ y - 2 = 3 (x - 3) \\ y - 2 = 3 x - 9 \\ y = 3 x - 7 - - - - (1) \\ Gradient of S T = \frac{6 - 1}{7 - 8} = - 5 \\ Equation of S T, \\ y - 1 = - 5 (x - 8) \\ y - 1 = - 5 x + 40 \\ y = - 5 x + 41 - - - - (2) \end{array}

Substitute (1) into (2),

3x – 7 = –5x + 41

8x = 48

x = 6

From (1),

y = 3(6) – 7 = 11

The coordinates of the point of intersection between lines PQ and ST = (6, 11).

Long Questions (Question 1)

Posted on April 21, 2020 by user

Question 1:

The diagram shows a trapezium PQRS. Given the equation of PQ is 2y – x – 5 = 0, find

(a) The value of w,

(b) the equation of PS and hence find the coordinates of P.

(c) The locus of M such that triangle QMS is always perpendicular at M.

Solution:
(a)

\begin{array}{l} Equation of P Q \\ 2 y - x - 5 = 0 \\ 2 y = x + 5 \\ y = \frac{1}{2} x + \frac{5}{2} \\ ∴ m_{P Q} = \frac{1}{2} \\ In a trapizium, m_{P Q} = m_{S R} \\ \frac{1}{2} = \frac{0 - (- 3)}{w - 4} \\ w - 4 = 6 \\ w = 10 \end{array}

(b)

\begin{array}{l} m_{P Q} = \frac{1}{2} \\ m_{P S} = - \frac{1}{m_{P Q}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Point S = (4, –3), m = –2

y – y₁ = m (x– x₁)

y – (–3) = –2 (x – 4)

y + 3 = –2x + 8

y = –2x + 5

Equation of PS is y = –2x + 5

PS is y = –2x + 5-----(1)

PQ is 2y = x + 5-----(2)

Substitute (1) into (2)

2 (–2x + 5) = x + 5

–4x + 10 = x + 5

–5x = –5

x = 1

From (1), y = –2(1) + 5

y = 3

Coordinates of point P = (1, 3).

(c)

\begin{array}{l} Let M = (x, y) \\ Given that △ Q M S is perpendicular at M \\ Thus △ Q M S = 90^{\circ} \\ (m_{Q M}) (m_{M S}) = - 1 \\ (\frac{y - 5}{x - 5}) (\frac{y - (- 3)}{x - 4}) = - 1 \\ (y - 5) (y + 3) = - 1 (x - 5) (x - 4) \\ y^{2} + 3 y - 5 y - 15 = - 1 (x^{2} - 4 x - 5 x + 20) \\ y^{2} - 2 y - 15 = - x^{2} + 9 x - 20 \\ x^{2} + y^{2} - 9 x - 2 y + 5 = 0 \end{array}

Hence, the equation of locus of the moving point M is

x² + y²– 9x – 2y + 5 = 0.

Short Questions (Question 6 & 7)

Posted on April 21, 2020 by user

Question 6:

The point M is (–3, 5) and the point N is (4, 7). The point P moves such that PM: PN = 2: 3. Find the equation of the locus of P.

Solution:

\begin{array}{l} Let P = (x, y) \\ P M : P N = 2 : 3 \\ \frac{P M}{P N} = \frac{2}{3} \\ 3 P M = 2 P N \\ 3 \sqrt{{(x - (- 3))}^{2} + {(y - 5)}^{2}} = 2 \sqrt{{(x - 4)}^{2} + {(y - 7)}^{2}} \end{array}

Square both sides to eliminate the square roots.

9[x² + 6x + 9 + y² – 10y + 25] = 4 [x²– 8x + 16 + y² – 14y + 49]

9x² + 54x + 9y² – 90y + 306 = 4x² – 32x + 4y² – 56y + 260

5x² + 5y²+ 86x – 34y + 46 = 0

Hence, the equation of the locus of point P is

5x² + 5y² + 86x – 34y + 46 = 0

Question 7:

Given the points A(0, 2) and B (6, 5). Find the equation of the locus of a moving point P such that the triangle APB always has a right angle at P.

Solution:

Let P = (x, y)

Given that triangle APB= 90^o, thus AP is perpendicular to PB.

Hence, (m_AP)(m_PB) = –1.

(m_AP)(m_PB) = –1

(\frac{y - 2}{x - 0}) (\frac{y - 5}{x - 6}) = - 1

(y – 2)(y – 5) = – x(x – 6)

y² – 7y + 10 = –x² + 6x

y² + x² – 6x – 7y + 10 = 0

Hence, the equation of the locus of point P is

y² + x² – 6x – 7y + 10 = 0.

Short Questions (Question 3, 4 & 5)

Posted on April 21, 2020 by user

Question 3:

The equation of the straight lines CD and EF are 5x + y – 4 = 0 and

\frac{x}{7} - \frac{y}{h} = 1

. If CD and EF are parallel, find the value of h.

Solution:

Two parallel lines have same gradient.

5x + y – 4 = 0

y = –5x + 4, m_CD= –5

For the straight line EF,

\begin{array}{l} \frac{x}{7} - \frac{y}{h} = 1 \\ m_{E F} = - (\frac{y -intercept}{x -intercept}) = - (\frac{- h}{7}) = \frac{h}{7} \\ m_{C D} = m_{E F} \\ - 5 = \frac{h}{7} \\ h = - 35 \end{array}

Question 4:

The straight line

\frac{x}{5} + \frac{y}{p} = 1

has a y-intercept of 3 and is parallel to the straight line y + qx = 0. Determine the value of p and of q.

Solution:

\begin{array}{l} Given y-intercept of the straight line \frac{x}{5} + \frac{y}{p} = 1 is 3, \\ ∴ p = 3 \\ Gradient of the straight line = - \frac{3}{5} \\ For another straight line y + q x = 0, y = - q x \\ As two parallel lines have same gradient, \\ - q = - \frac{3}{5} \\ q = \frac{3}{5} \end{array}

Question 5:

The equations of two straight lines

\frac{y}{7} + \frac{x}{4} = 1

y = 4x + 21. Determine whether the lines are perpendicular to each other.

Solution:

\begin{array}{l} For the straight line \frac{y}{7} + \frac{x}{4} = 1, gradient = - \frac{7}{4} \\ For the straight line 7 y = 4 x + 21, \\ y = \frac{4}{7} x + 3, gradient = \frac{4}{7} \\ - \frac{7}{4} \times \frac{4}{7} = - 1 \end{array}

Hence, the two straight lines are perpendicular to each other.

Short Questions (Question 1 & 2)

Posted on April 21, 2020 by user

Question 1:

The vertices of a triangle are P (6, 1), Q (5, 6) and R (m, -1). Given that the area of the triangle is 31 unit², find the values of m.

Solution:

\begin{array}{l} Area of △ P Q R = 31 \\ \frac{1}{2} | \begin{array}{l} 6     5 m \\ 1     6 - 1 \end{array} \begin{array}{l} 6 \\ 1 \end{array} | = 31 \\ | (6) (6) + (5) (- 1) + (m) (1) \\ - (1) (5) - (6) (m) - (- 1) (6) | = 62 \\ | 36 - 5 + m - 5 - 6 m + 6 | = 62 \\ | 32 - 5 m | = 62 \\ 32 - 5 m = \pm 62 \\ - 5 m = 62 - 32 or - 5 m = - 62 - 32 \\ m = - 6 or m = \frac{94}{5} \end{array}

Question 2:

The points P (3m, m), Q (t, u) and R (3t, 2u) lie on a straight line. Q divides PR in the ratio 3 : 2. Express t in terms of u.

Solution:

\begin{array}{l} (\frac{(3 m) (2) + (3 t) (3)}{3 + 2}, \frac{(m) (2) + (2 u) (3)}{3 + 2}) = (t, u) \\ \frac{6 m + 9 t}{5} = t \\ 6 m + 9 t = 5 t \\ 6 m = - 4 t \\ m = - \frac{2}{3} t \to (1) \\ \frac{2 m + 6 u}{5} = u \\ 2 m + 6 u = 5 u \\ 2 m = - u \\ From (1), \\ 2 (- \frac{2 t}{3}) = - u \\ t = \frac{3}{4} u \end{array}

6.6 Equation of a Locus

Posted on April 21, 2020 by user

6.6 Equation of a Locus

1. The equation of the locus of a moving point P(x, y) which is always at a constant distance (r) from a fixed point (x₁, y₁) is:

2. The equation of the locus of a moving point P(x, y) which is always at a constant distance from two fixed points (x₁, y₁) and (x₁, y₁) with a ratio is:

3. The equation of the locus of a moving point P (x, y) which is always equidistant from two fixed points A and B is the perpendicular bisector of the straight line AB.

Example 1

Find the equation of the locus of a moving point P(x, y) which is always at a distance of 5 units from a fixed point Q (2, 4).

Solution:

(x – x₁)²+ (y – y₁)² = r²

(x – 2)² + (y – 4)² = 5²

x² – 4x + 4 + y² – 8y + 16 = 25

x² + y²– 4x – 8y – 5 = 0

Example 2

Find the equation of the locus of a moving point P(x, y) which is always equidistant from points A (-2, 3) and B (4, -1).

Solution:

\begin{array}{l} Given P A = P B \\ \sqrt{{(x - (- 2))}^{2} + {(y - 3)}^{2}} = \sqrt{{(x - 4)}^{2} + {(y - (- 1))}^{2}} \\ Square both sides to eliminate the square roots . \\ {(x + 2)}^{2} + {(y - 3)}^{2} = {(x - 4)}^{2} + {(y + 1)}^{2} \\ x^{2} + 2 x + 4 + y^{2} - 6 y + 9 = x^{2} - 8 x + 16 + y^{2} + 2 y + 1 \\ 10 x - 8 y - 4 = 0 \\ Hence, the equation of the locus of point P is \\ 10 x - 8 y - 4 = 0 \end{array}

Example 3

A (2, 0) and B (0, -2) are two fixed points. Point P moves with a ratio so that AP: PB = 1: 2. Find the equation of the locus of point P.

Solution:

\begin{array}{l} A P : P B = 1 : 2 \\ \frac{A P}{P B} = \frac{1}{2} \\ 2 A P = P B \\ 2 \sqrt{{(x - 2)}^{2} + {(y - 0)}^{2}} = \sqrt{{(x - 0)}^{2} + {(y - (- 2))}^{2}} \\ Square both sides to eliminate the square roots . \\ 4 [{(x - 2)}^{2} + y^{2}] = x^{2} + {(y + 2)}^{2} \\ 4 (x^{2} - 4 x + 4 + y^{2}) = x^{2} + y^{2} + 4 y + 4 \\ 4 x^{2} - 16 x + 16 + 4 y^{2} = x^{2} + y^{2} + 4 y + 4 \\ 3 x^{2} + 3 y^{2} - 16 x - 4 y + 12 = 0 \\ Hence, the equation of the locus of point P is \\ 3 x^{2} + 3 y^{2} - 16 x - 4 y + 12 = 0 \end{array}

6.5 Parallel Lines and Perpendicular Lines

Posted on April 21, 2020 by user

6.5 Parallel Lines and Perpendicular Lines

(A) Parallel Lines
1. If two straight lines are parallel, they have same gradient.

In the above diagram, if straight line L₁is parallel to straight line L₂, gradient of L₁= gradient of L₂

m_{1} = m_{2}

Example 1:

Given that the equation of a straight line parallel to x + 8y= 40 and passes through the point A(2, 3k) and B (-6, 4k²), find the values of k.

Solution:

\begin{array}{l} x + 8 y = 40 \\ 8 y = - x + 40 \\ y = - \frac{1}{8} x + 5 \\ gradient m_{1} = - \frac{1}{8} \\ Given a straight line passes through \\ point A and point B is parallel to x + 8 y = 40, \\ ∴ m_{1} = m_{2} \\ - \frac{1}{8} = \frac{4 k^{2} - 3 k}{- 6 - 2} \\ 8 = 32 k^{2} - 24 k \\ 1 = 4 k^{2} - 3 k \\ 4 k^{2} - 3 k - 1 = 0 \\ (4 k + 1) (k - 1) = 0 \\ 4 k + 1 = 0 or k - 1 = 0 \\ k = - \frac{1}{4} or k = 1 \end{array}

(B) Perpendicular Lines
1. If two lines are perpendicular to each other, the product of their gradients is –1.

In the above diagram, if straight line L₁is perpendicular to straight line L₂,

gradient of L₁× gradient of L₂= –1

m_{1} \times m_{2} = - 1

Example 2:

Given that points P (–2, 4), Q (4, 2), R (–1, –3) and S (2, 6), show that PQ is perpendicular to RS.

Solution:

\begin{array}{l} m_{P Q} = \frac{2 - 4}{4 - (- 2)} = - \frac{1}{3} \\ m_{R S} = \frac{6 - (- 3)}{2 - (- 1)} = 3 \\ (m_{P Q}) (m_{R S}) = (- \frac{1}{3}) (3) = - 1 \end{array}

Hence, PQ is perpendicular to RS.