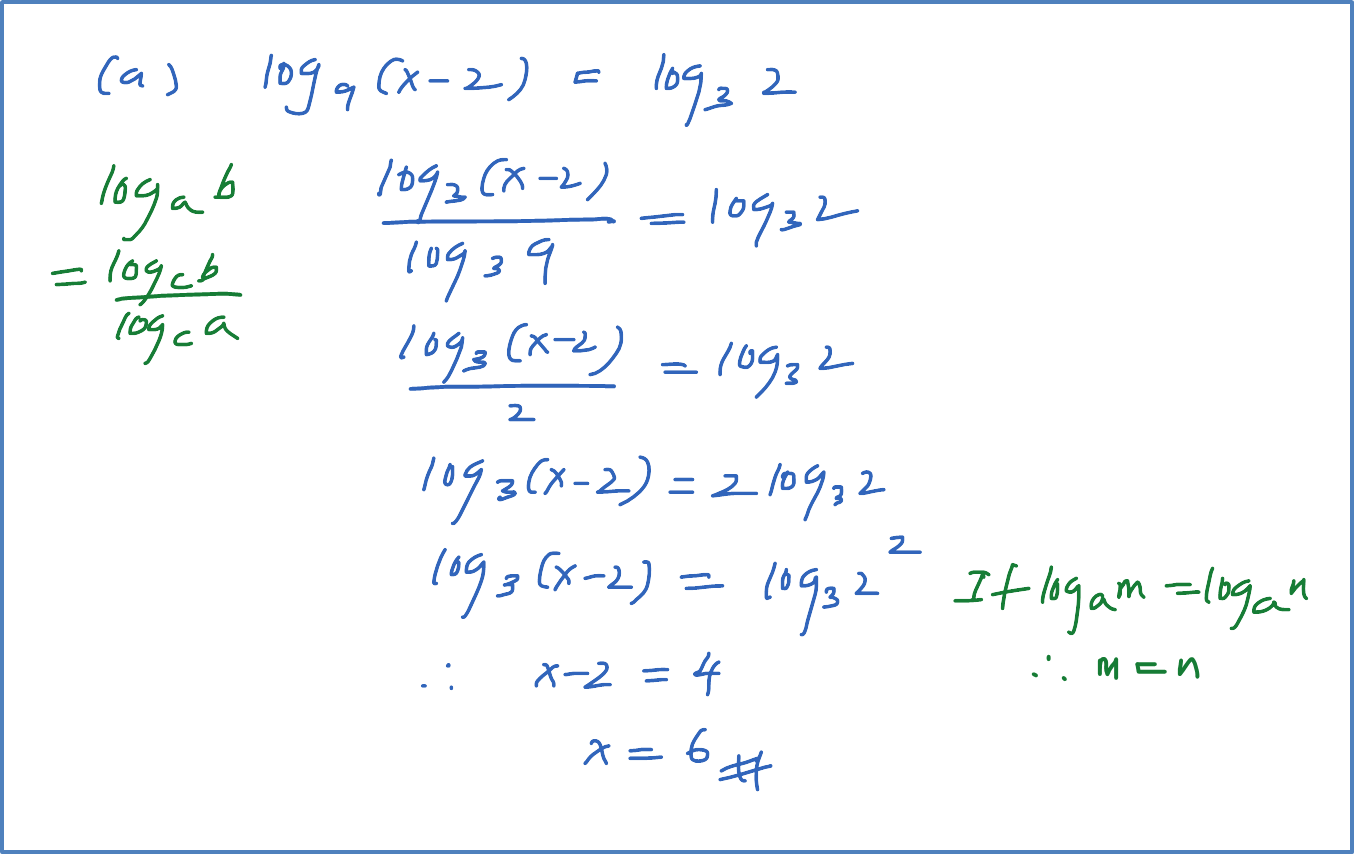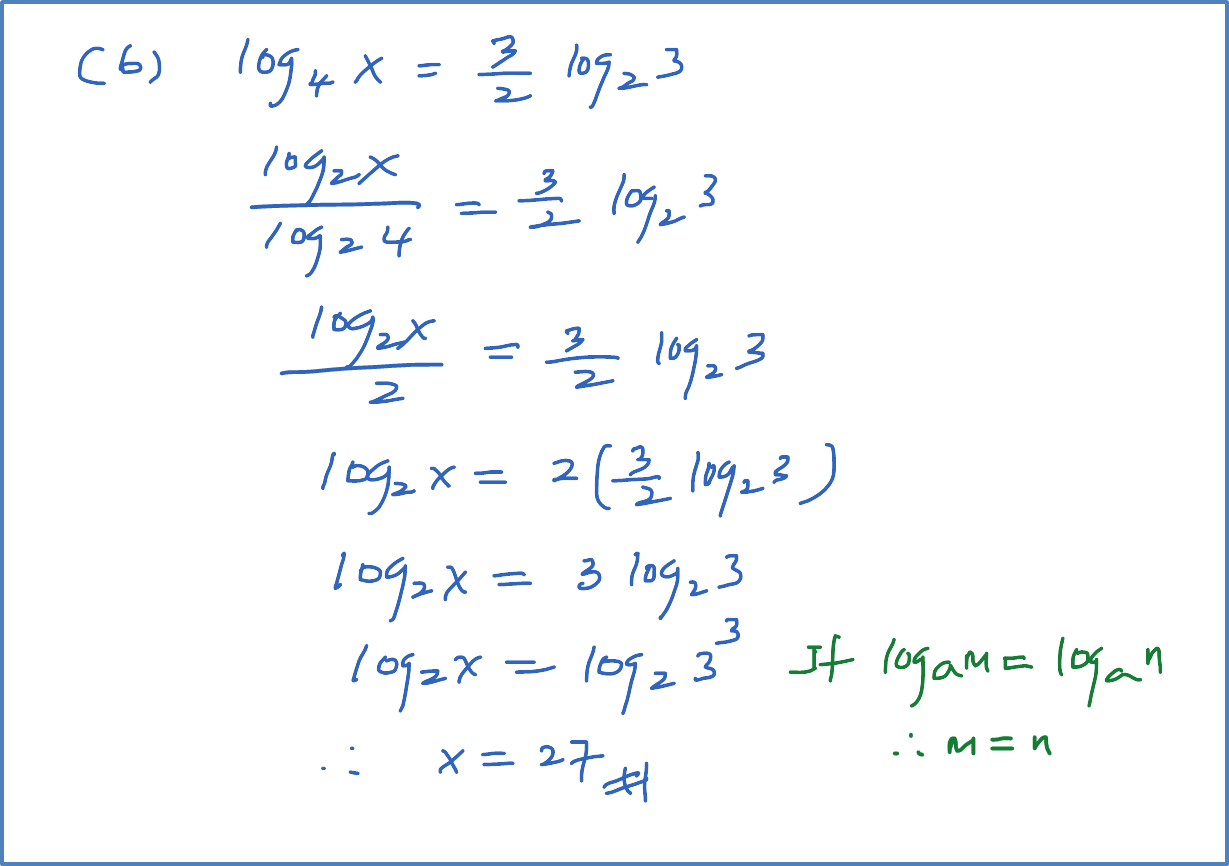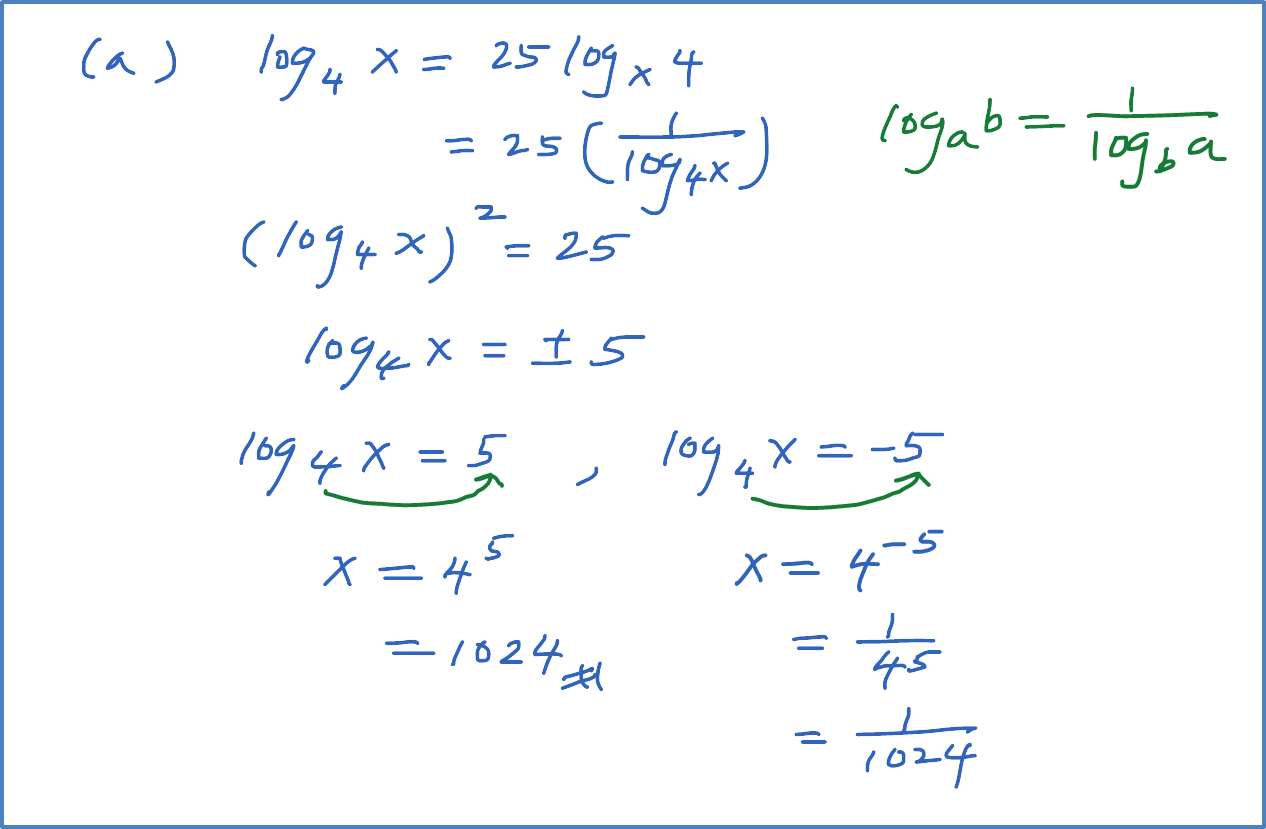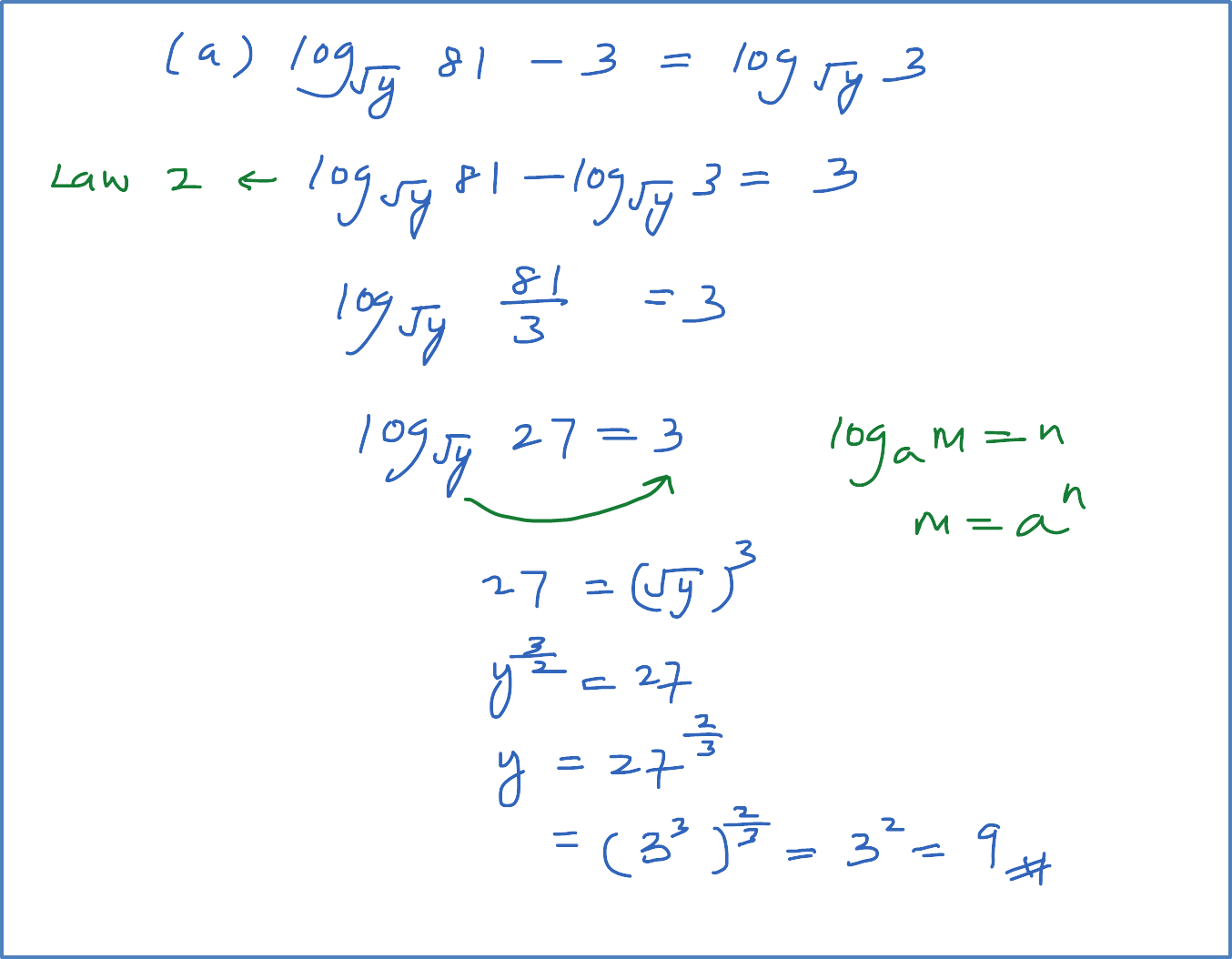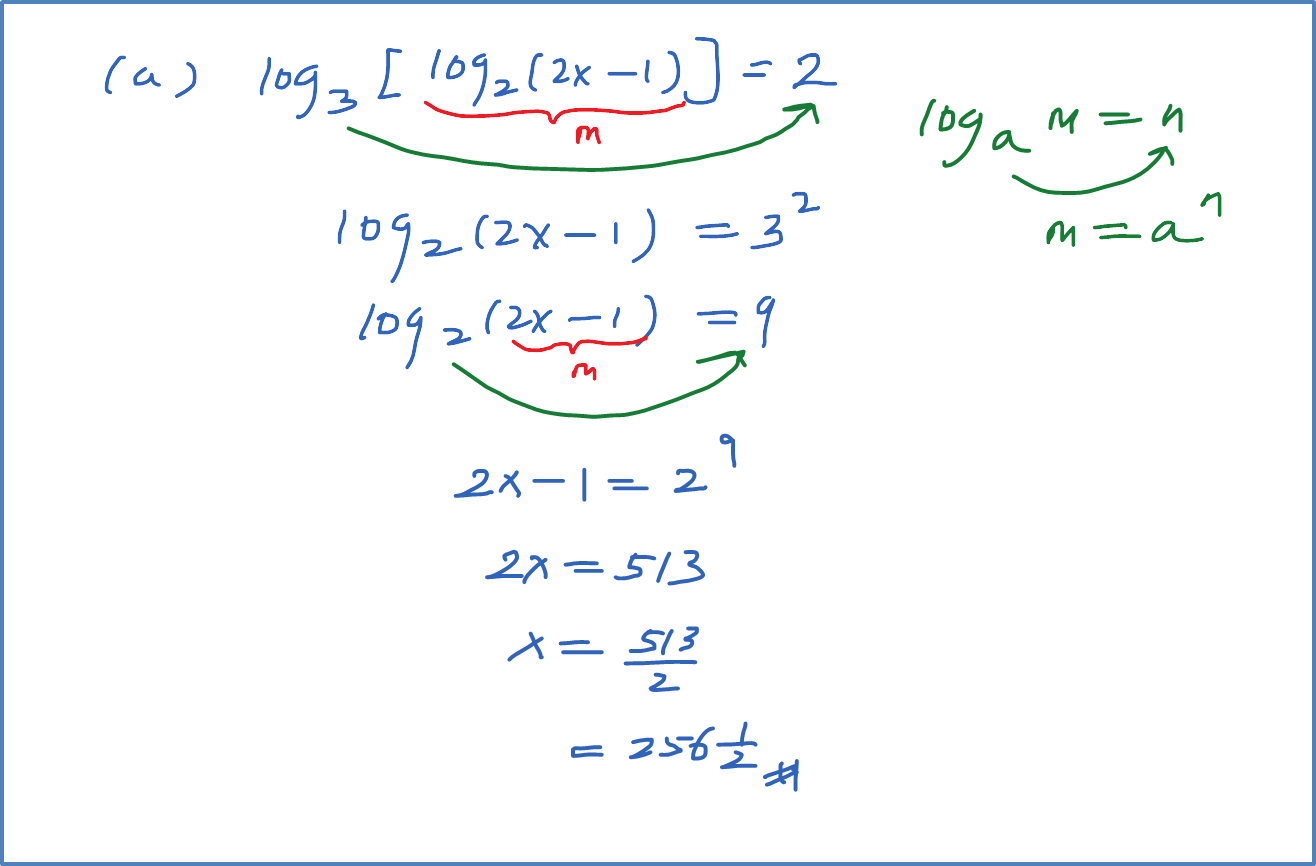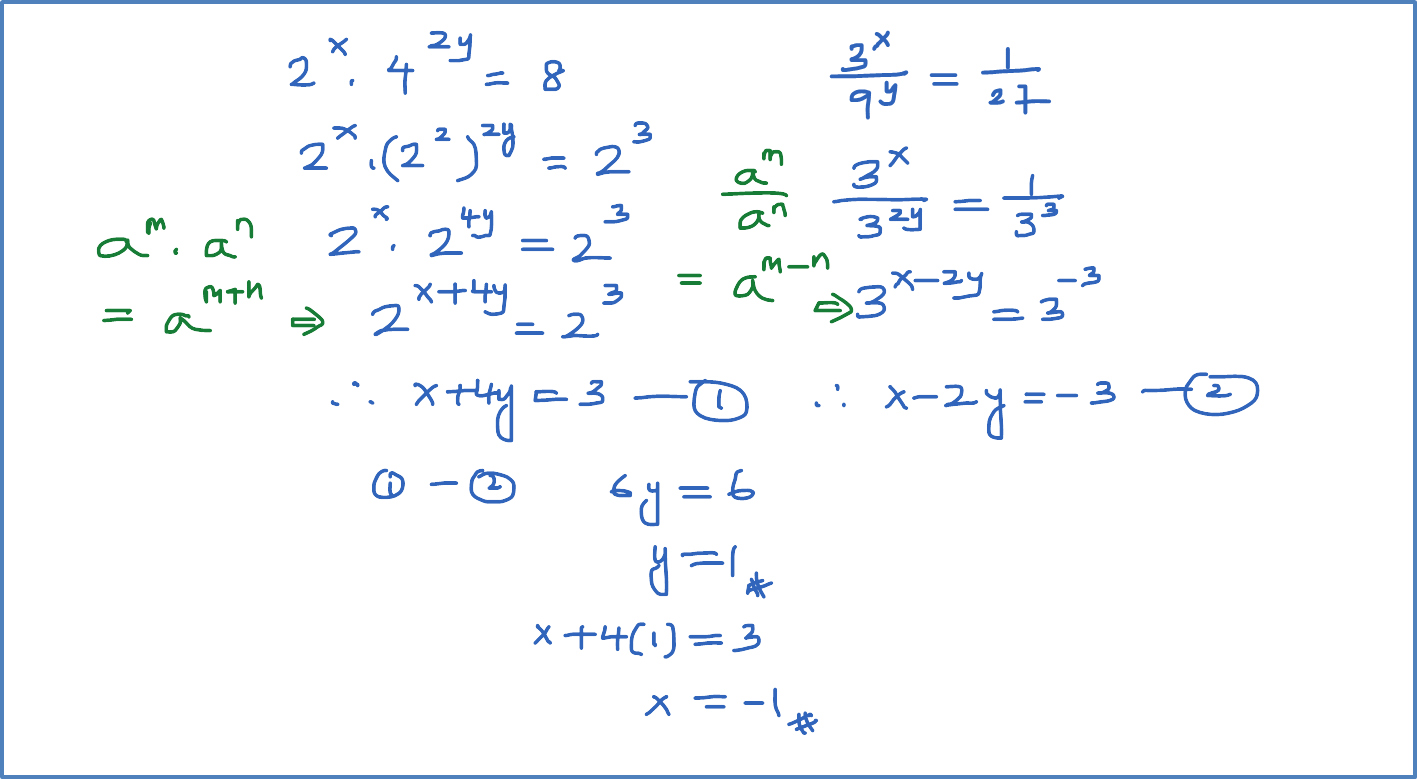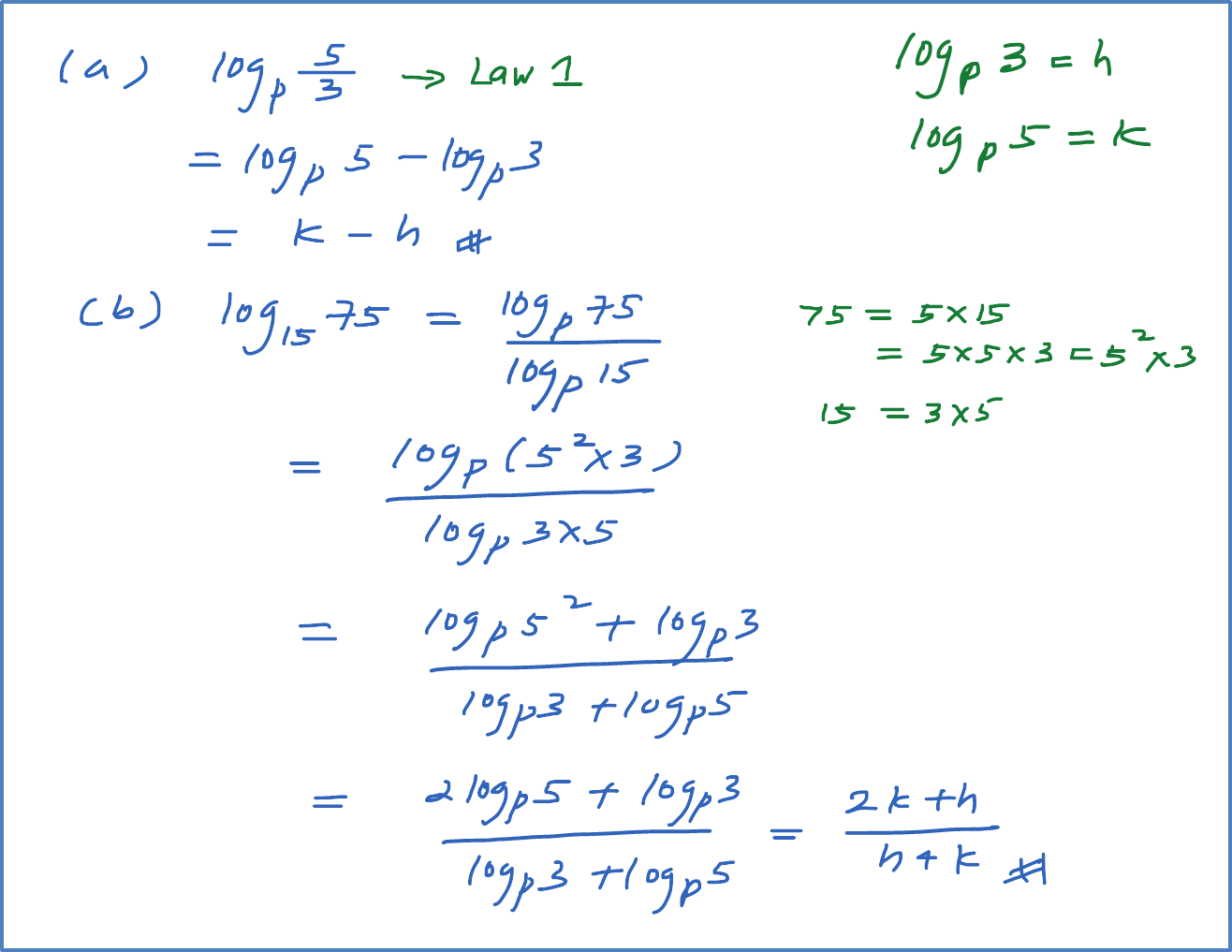Loading [MathJax]/jax/output/CommonHTML/jax.js

Short Questions (Question 1 – 4)

Posted on April 21, 2020 by user

Question 1

Solve the equation, log₃ [log₂(2x – 1)] = 2

Solution:

log₃ [log₂ (2x – 1)] = 2 ← (if log _aN = x, N = a^x)

log₂ (2x – 1) = 3²
log₂ (2x – 1) = 9

2x – 1 = 2⁹

x = 256.5

Question 2

Solve the equation,

$l o g_{16} [l o g_{2} (5 x - 4)] = l o g_{9} \sqrt{3}$

Solution:

$\begin{array}{l} l o g_{16} [l o g_{2} (5 x - 4)] = l o g_{9} \sqrt{3} \\ l o g_{16} [l o g_{2} (5 x - 4)] = \frac{1}{4} \leftarrow \begin{array}{l} \log_{9} \sqrt{3} = \log_{9} 3^{\frac{1}{2}} = \frac{1}{2} \log_{9} 3 \\ = \frac{1}{2} (\frac{1}{\log_{3} 9}) = \frac{1}{2} (\frac{1}{2}) = \frac{1}{4} \end{array} \\ l o g_{2} (5 x - 4) = 16^{\frac{1}{4}} \\ l o g_{2} (5 x - 4) = 2 \\ 5 x - 4 = 2^{2} \\ 5 x = 8 \\ x = \frac{8}{5} \end{array}$

Question 3

Solve the equation,

$5^{\log_{4} x} = 125$

Solution:

$\begin{array}{l} 5^{\log_{4} x} = 125 \\ \log_{5} 5^{\log_{4} x} = \log_{5} 125 \leftarrow put log for both side \\ (\log_{4} x) (\log_{5} 5) = 3 \\ (\log_{4} x) (1) = 3 \\ x = 4^{3} = 64 \end{array}$

Question 4

Solve the equation,

$5^{\log_{5} (x + 1)} = 9$

Solution:

$\begin{array}{l} 5^{\log_{5} (x + 1)} = 9 \\ \log_{5} 5^{^{\log_{5} (x + 1)}} = \log_{5} 9 \\ \log_{5} (x + 1) . \log_{5} 5 = \log_{5} 9 \\ \log_{5} (x + 1) = \log_{5} 9 \\ x + 1 = 9 \\ x = 8 \end{array}$

5.4 Equations Involving Logarithms (Example 4 & 5)

Posted on April 21, 2020 by user

Example 4
Solve the following equation :
(a)

$\log_{9} (x - 2) = \log_{3} 2$
(b)

$\log_{4} x = \frac{3}{2} \log_{2} 3$

Example 5
Solve the following :
(a)

$\log_{4} x = 25 \log_{x} 4$
(b)

$\log_{2} 5 \sqrt{x} + \log_{4} 16 x = 6$

5.4 Equations Involving Logarithms (Example 2 & 3)

Posted on April 21, 2020 by user

Example 2
Solve the following equation:
(a)

$\log_{\sqrt{y}} 81 - 3 = \log_{\sqrt{y}} 3$
(b)

$2 \log_{2} x - \log_{2} (\frac{x}{2} - 1) - 4 = 0$

Example 3
Sole the following equation:
(a)

$\log_{3} [\log_{2} (2 x - 1)] = 2$
(b)

$\log_{16} [\log_{2} (5 x - 4)] = \log_{9} \sqrt{3}$

5.4 Equations Involving Logarithms

Posted on April 21, 2020 by user

METHOD:

For two logarithms of the same base, if $\log_{a} m = \log_{a} n$ , then m = n .
Convert to index form, if $\log_{a} m = n$ , then m = aⁿ.

Example 1
Solve the following equation:
(a)

$\log_{3} 2 + \log_{3} (x + 5) = \log_{3} (3 x - 1)$
(b)

$\log_{2} 8 x - 3 = \log_{2} (2 x - 1)$
(c)

$3 \log_{x} 2 + 2 \log_{x} 4 - \log_{x} 256 = - 1$

5.3 Equations Involving Indices (Example 5)

Posted on April 21, 2020 by user

Example 5 (Unequal Base – put log both sides):
Solve each of the following.
(a)

$3^{x + 1} = 7$
(b)

$2 (3^{x}) = 5$
(c)

$2^{x} {.3}^{x} = 9^{x - 4}$
(d)

$5^{x - 1} {.3}^{x + 2} = 10$

5.3 Equations Involving Indices (Example 4)

Posted on April 21, 2020 by user

Example 4 (Index Equation - Substitution)
Solve each of the following.
(a)

$3^{x - 1} + 3^{x} = 12$
(b)

$2^{x} + 2^{x + 3} = 72$
(c)

$4^{x + 1} + 2^{2 x} = 20$

5.3 Equations Involving Indices (Example 3)

Posted on April 21, 2020 by user

Example 3 (Index Equation - Equal Base)
Solve each of the following.
(a)

$27 (81^{3 x}) = 1$
(b)

$\sqrt{81^{n + 2}} = \frac{1}{3^{n} 27^{n - 1}}$
(c)

$8^{x - 1} = \frac{4}{\sqrt{2^{x + 3}}}$

5.3 Equations Involving Indices

Posted on April 21, 2020 by user

METHOD:

Comparison of indices or base

If the base are the same , when $a^{x} = a^{y}$ , then x = y
If the index are the same , when $a^{x} = b^{x}$ , then a = b

Using common logarithm (If base and index are NOT the same)

$\begin{array}{l} a^{x} = b \Rightarrow \lg a^{x} = \lg b \\ x = \frac{\lg b}{\lg a} \end{array}$

Example 1 (Index Equation - Equal base)
Solve each of the following.
(a)

$16^{x} = 8$
(b)

$9^{x} {.3}^{x - 1} = 81$
(c)

$5^{n + 1} = \frac{1}{125^{n - 1}}$

Example 2 (Solving index equation simultaneously)
Solve the following simultaneous equations.

$2^{x} {.4}^{2 y} = 8$

$\frac{3^{x}}{9^{y}} = \frac{1}{27}$

5.2b Change of Base of Logarithms (Example 5)

Posted on April 21, 2020 by user

Example 5:

Given that log₂ 3 = 1.585 and log₂ 5 = 2.322, evaluate the following.

log₈ 15
log₅ 0.6
log₁₅ 30
log₁₆ 45

Solution:

5.2b Change of Base of Logarithms (Example 3 & 4)

Posted on April 21, 2020 by user

Example 3
Given that

$\log_{p} 3 = h$ and

$\log_{p} 5 = k$ , express the following in term of h and or k.
(a)

$\log_{p} \frac{5}{3}$

(b)

$\log_{15} 75$

Example 4
Given that

$\log_{3} x = b$ , express

$\log_{x} 9 x$ in term of b.