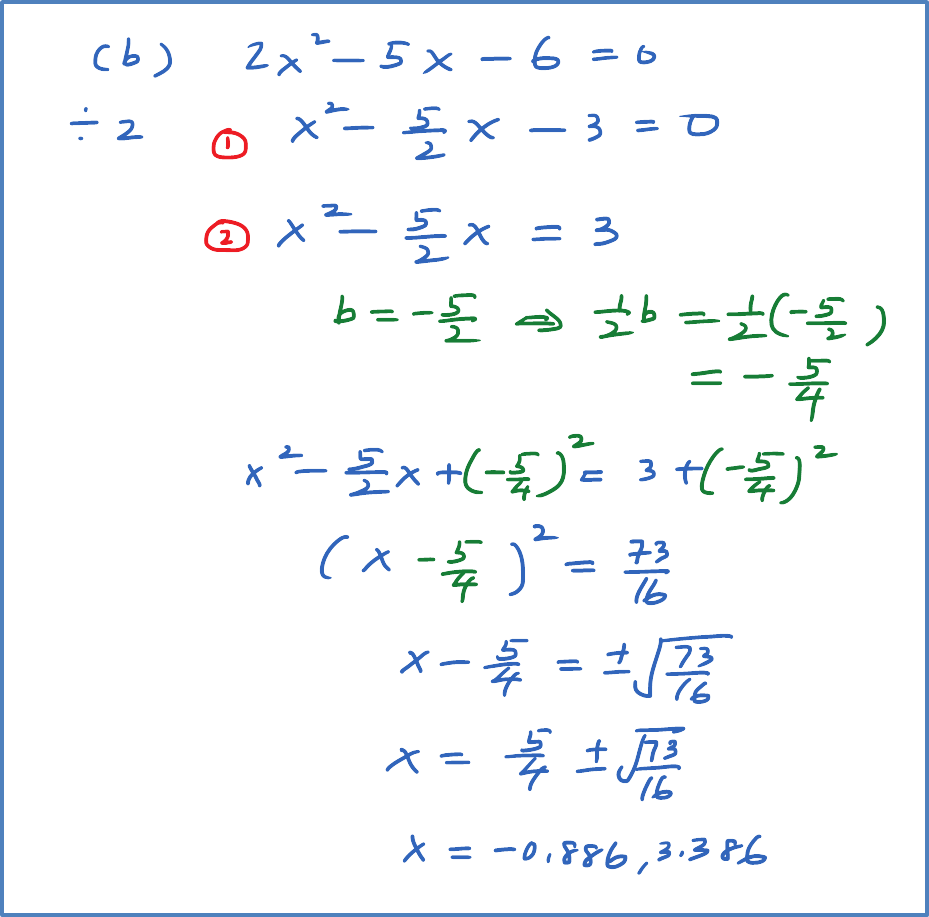Home › Archive for SPM Add Maths › Page 51

SPM Add Maths

3.3a Finding the Maximum and Minimum Points of Quadratic Function using Completing the Square (Examples)

Posted on by
Example 1 
Find the maximum or minimum value of each of the following quadratic function by completing the squares.  In each case, state the value of x at which the function is maximum or minimum.  And also, state the maximum or minimum point and axis of symmetry for each case.

(a) f ( x ) = x 2 + 6 x + 7
(b) f ( x ) = 2 x 2 − 6 x + 7
(c) f ( x ) = 5 − 2 x − x 2
(d) f ( x ) = 4 + 12 x − 3 x 2













3.3 Finding the Maximum and Minimum Points of Quadratic Function using Completing the Square

Posted on by
Steps to convert general form of Quadratic Function into completing the square form

General form of quadratic function : f ( x ) = a x 2 + b x + c

Completing the square form : f ( x ) = a ( x + p ) 2 + q

Step 1 : Make sure the coefficient x 2 is 1, if not factorize.
Step 2 : Insert + ( c o e f f i c i e n t ​ ​ − o f ​ x 2 ) 2 − ( c o e f f i c i e n t ​ ​ − o f ​ x 2 ) 2
Step 3 : Completing the square [convert f ( x ) = a x 2 + b x + c into f ( x ) = a ( x + p ) 2 + q .]





3.2a Finding the Maximum/minimum and Axis of Symmetry of a Quadratic Function

Posted on by
Example 1
State the maximum or minimum value of   for each of the following quadratic function and state the value of x at which the function is maximum or minimum.  Find the maximum or minimum point and finally state axis of symmetry for each case.

(a) f ( x ) = − 2 ( x − 3 ) 2 + 4
(b) f ( x ) = 3 ( x − 4 ) 2 + 10
(c) f ( x ) = − 3 ( x + 2 ) 2 − 9
(d) f ( x ) = − 8 + 2 ( x + 5 ) 2






Correction for part (d) of the question,
when x + 5 = 0, x = -5
minimum point is (-5, -8)
Axis of symmetry, x = -5




3.1 Graph of Quadratic Functions

Posted on by
  1. The graph of quadratic function is parabola.
  2. When the coefficient of x2 is positive the graph is a parabola with ∪ shape.
  3. When the coefficient of x2 is negative the graph is a parabola with ∩ shape.

(A) Axis of Symmetry

The axis of symmetry is a vertical line passing through the maximum or minimum point of the parabola.

 

 

 

(A) General Form of Quadratic Function

Posted on by

3.1 General Form of Quadratic Function
General form of a quadratic function is f ( x ) = a x 2 + b x + c where a, b, and c are constants and a ≠ 0, and x as a variable.

Example:
Determine which of the following is a quadratic function.
  1. f ( x ) = ( 5 x − 3 ) ( 3 x + 8 )
  2. f ( x ) = 2 ( 3 x + 8 )
  3. f ( x ) = 5 2 x 2
Answer:
(a)
  f ( x ) = ( 5 x − 3 ) ( 3 x + 8 ) f ( x ) = 15 x 2 + 40 x − 9 x − 24 f ( x ) = 15 x 2 + 31 x − 24
Quadratic function

(b)
f ( x ) = 2 ( 3 x + 8 ) f ( x ) = 6 x + 16
Not quadratic function


(c) Not quadratic function

SPM Practice (Paper 1)

Posted on by
Question 11:
The quadratic equation x 2 −4x−1=2p(x−5) , where p is a constant, has two equal roots. Calculate the possible values of p.

Solution:




Question 12:
Find the range of values of k for which the equation x 2 −2kx+ k 2 +5k−6=0 has no real roots.

Solution:




Question 13:
Find the range of values of p for which the equation 5 x 2 +7x−3p=6 has no real roots.

Solution:

SPM Practice (Paper 1)

Posted on by
Question 6:
Write and simplify the equation whose roots are the reciprocals of the roots of 3 x 2 +2x−1=0 , without solving the given equation.

Solution:





Question 7:
Find the value of p if one root of x 2 +px+8=0 is the square of the other.

Solution:





Question 8:
If one root of 2 x 2 +px+9=0 is twice the other, find the values of p.

Solution:


SPM Practice (Paper 1)

Posted on by

Question 1:
Solve the following quadratic equations by factorisation.
(a)  x 2 −5x−10=−4 (b) 3−x−2 x 2 =0 (c) 11a=2 a 2 +12 (d)  2x+7 3x−2 =x

Solution:








Question 2:
Solve the following quadratic equations by completing the square.
(a) 5 x 2 +10x−3=0 (b) 2 x 2 −5x−6=0

Solution: