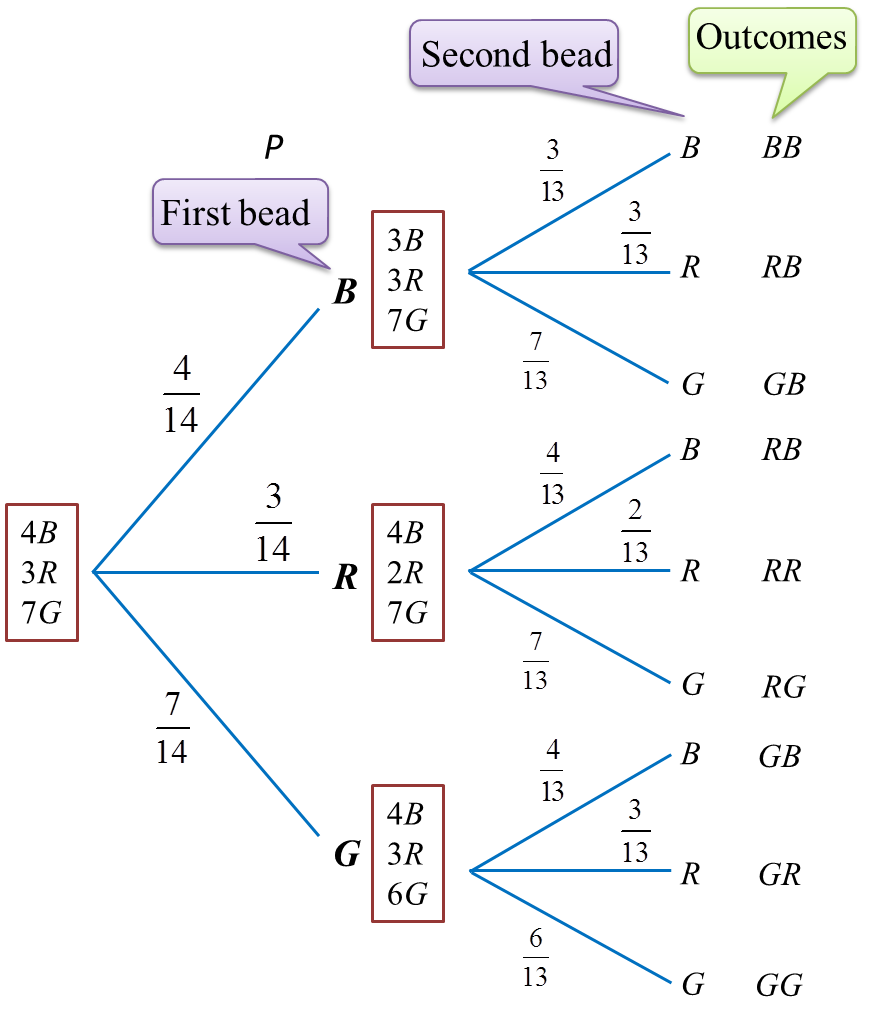
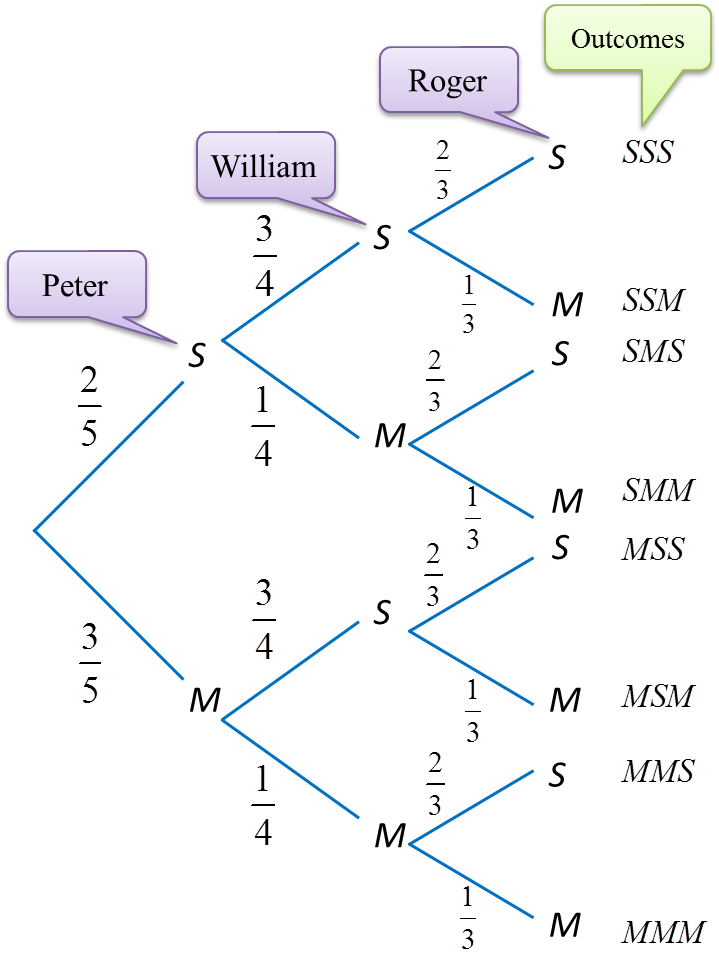
Question 4:
The events A and B are not independent.
Given P(A)=35,P(B)=14 and P(A∪B)=15, find(a) P[(A∪B)'],(b) P(A∩B).
Solution:
(a)
P[(A∪B)']=1−P(A∪B) =1−15 =45
(b)
P(A∩B)=P(A)+P(B)−P(A∪B) =35+14−15 =1320
The events A and B are not independent.
Given P(A)=35,P(B)=14 and P(A∪B)=15, find(a) P[(A∪B)'],(b) P(A∩B).
Solution:
(a)
P[(A∪B)']=1−P(A∪B) =1−15 =45
(b)
P(A∩B)=P(A)+P(B)−P(A∪B) =35+14−15 =1320
Question 5 (3 marks):
A biased cube dice is thrown. The probability of getting the number ‘4’ is 116 and the probabilities of getting other than ‘4’ are equal to each other.
If the dice is thrown twice, find the probability of getting two different numbers.
Give your answer in the simplest fraction form.
Solution:
P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1Given probabilities of getting numbers are equal.x+x+x+116+x+x=15x=1−1165x=1516x=316P(Same numbers)=P(1, 1)+P(2, 2)+P(3, 3)+P(4, 4)+P(5, 5)+P(6, 6)=(x×x)+(x×x)+(x×x)+(116×116)+(x×x)+(x×x)=5x2+1256=5(316)2+1256=23128P(Two different numbers)=1−23128=105128
A biased cube dice is thrown. The probability of getting the number ‘4’ is 116 and the probabilities of getting other than ‘4’ are equal to each other.
If the dice is thrown twice, find the probability of getting two different numbers.
Give your answer in the simplest fraction form.
Solution:
P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1Given probabilities of getting numbers are equal.x+x+x+116+x+x=15x=1−1165x=1516x=316P(Same numbers)=P(1, 1)+P(2, 2)+P(3, 3)+P(4, 4)+P(5, 5)+P(6, 6)=(x×x)+(x×x)+(x×x)+(116×116)+(x×x)+(x×x)=5x2+1256=5(316)2+1256=23128P(Two different numbers)=1−23128=105128