8.2b Standard Normal Distribution Tables

Posted on April 23, 2020 by user

8.2b Standard Normal Distribution Tables

The characteristics of the tables of the standard normal distribution, N (0, 1) are:

Case 1

P (Z > a) is the area of the shaded region in the above diagram.

Case 2

P (–∞ < Z < ∞) = 1

Case 3

P (Z > 0) = P (Z < 0) = 0.5

Case 4

P (Z > a) = P (Z < –a)

8.2 Normal Distribution

Posted on April 23, 2020 by user

8.2 Normal Distribution

(A) Continuous Random Variable

Continuous random variable is a variable that can take any infinite value in a certain range.

(B) Normal Distribution

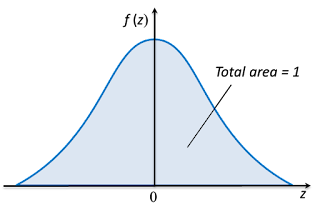
1. A continuous random variable, X, is normally distributed if the graph of its probability function has the following properties.

· Its curve has a bell shape and it is symmetrical at the line x = µ.

· Its curve has a maximum value at x = µ.

· The area enclosed by the normal curve and the x-axis is 1.

2. The notation of X being normally distributed with a mean, µ and a variance, σ² is X ~ N (µ, σ²).

(C) Standard Normal Distribution

If a normal random variable, X, has a mean, µ = 0 and a standard deviation, σ = 1, then X follows a standard normal distribution, i.e. X ~ N (0, 1).

(D) Curve of a Standard Normal Distribution

1. The curve of a standard normal distribution has the following properties.

· Its curve is symmetrical at the vertical line that passes through the mean, µ = 0 and has a variance, σ² = 1.

· Its curve has a maximum value at Z = 0.

· The area enclosed by the standard normal curve and the z-axis is 1.

(E) Converting a Normal Distribution to Standard Normal Distribution

A normal distribution can be converted to the standard normal distribution using the following formula:

Z = \frac{x - μ}{σ}

where,

Z = standard score or z - score

X = value of a normal random variable

µ = mean of a normal distribution

σ = standard deviation of a normal distribution

Long Questions (Question 1 & 2)

Posted on April 23, 2020 by user

Question 1:

In a school examination, 2 students out of 5 students failed Chemistry.

(a) If 6 students are chosen at random, find the probability that not more than 2 students failed Chemistry.

(b) If there are 200 Form 4 students in that school, find the mean and standard deviation of the number of students who failed Chemistry.

Solution:
(a)

\begin{array}{l} X - Number of students who failed Chemistry . \\ X ~ B (n, p) \\ X ~ B (6, \frac{2}{5}) \\ P (X = r) = {}^{n}c_{r} . p^{r} . q^{n - r} \\ P (X \leq 2) \\ = P (X = 0) + P (X = 1) + P (X = 2) \\ = {}^{6}C_{0} {(\frac{2}{5})}^{0} {(\frac{3}{5})}^{6} + {}^{6}C_{1} {(\frac{2}{5})}^{1} {(\frac{3}{5})}^{5} + {}^{6}C_{2} {(\frac{2}{5})}^{2} {(\frac{3}{5})}^{4} \\ = 0.0467 + 0.1866 + 0.3110 \\ = 0.5443 \end{array}

(b)

\begin{array}{l} X ~ B (n, p) \\ X ~ B (200, \frac{2}{5}) \\ Mean of X \\ = n p = 200 \times \frac{2}{5} = 80 \\ Standard deviation of X \\ = \sqrt{n p q} \\ = \sqrt{200 \times \frac{2}{5} \times \frac{3}{5}} \\ = \sqrt{48} \\ = 6.93 \end{array}

Question 2:

5% of the supply of mangoes received by a supermarket are rotten.

(a) If a sample of 12 mangoes is chosen at random, find the probability that at least two mangoes are rotten.

(b) Find the minimum number of mangoes that have to be chosen so that the probability of obtaining at least one rotten mango is greater than 0.85.

Solution:
(a)

X ~ B (12, 0.05)

1 – P (X ≤ 1)

= 1 – [P (X = 0) + P (X = 1)]

= 1 – [

C_{0}

(0.05)⁰ (0.95)¹² +

C_{1}

(0.05)¹ (0.95)¹¹]

= 1 – 0.8816

= 0.1184

(b)

P (X ≥ 1) > 0.85

1 – P (X = 0) > 0.85

P (X = 0) < 0.15

C_{0}

(0.05)⁰(0.95)ⁿ< 0.15

n lg 0.95 < lg 0.15

n > 36.98

n = 37

Therefore, the minimum number of mangoes that have to be chosen so that the probability of obtaining at least one rotten mango is greater than 0.85 is 37.

8.2a Z-Score Of A Normal Distribution

Posted on April 23, 2020 by user

8.2a z–Score of a Normal Distribution

Example:

(a) A normal distribution has a mean, µ = 50 and a standard deviation σ = 10. Calculate the standard score of the value X = 35.

(b) The masses of Form 5 students of a school are normally distributed with a mean of 60 kg and a standard deviation of 15 kg.

Find

(i) the standard score of the mass of 65 kg,

(ii) the mass of a student that corresponds to the standard score of – ½.

Solution:

(a)

X ~ N (µ, σ²).

X ~ N (50, 10²)

Z = \frac{X - μ}{σ} = \frac{35 - 50}{10} = - 1.5

(b)(i)

X – Mass of a Form 5 student

X ~ N (µ, σ²).

X ~ N (60, 15²)

Z = \frac{X - μ}{σ} = \frac{65 - 60}{15} = \frac{1}{3}

Hence, the standard score of the mass of 65 kg is ⅓.

(b)(ii)

Z = – ½,

\begin{array}{l} Z = \frac{X - μ}{σ} \\ - \frac{1}{2} = \frac{X - 60}{15} \\ X - 60 = - \frac{1}{2} (15) \\ X = 52.5 \end{array}

Hence, the mass of a Form 5 student that corresponds to the standard score of – ½ is 52.5 kg.

Short Questions (Question 1 & 2)

Posted on April 23, 2020 by user

Question 1:

Diagram below shows the graph of a binomial distribution of X.

(a) the value of h,

(b) P (X ≥ 3)

Solution:

(a)

P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4) = 1

\begin{array}{l} \frac{1}{16} + \frac{1}{4} + h + \frac{1}{4} + \frac{1}{16} = 1 \\ h = 1 - \frac{5}{8} \\ h = \frac{3}{8} \end{array}

(b)

P (X ≥ 3) = P (X = 3) + P (X = 4)

P (X \geq 3) = \frac{1}{4} + \frac{1}{16} = \frac{5}{16}

Question 2:

The random variable X represents a binomial distribution with 10 trails and the probability of success is ¼.

(a) the standard deviation of the distribution,

(b) the probability that at least one trial is success.

Solution:

(a)

n = 10, p = ¼

\begin{array}{l} Standard deviation = \sqrt{n p q} \\ = \sqrt{10 \times \frac{1}{4} \times \frac{3}{4}} \\ = 1.875 \end{array}

(b)

\begin{array}{l} P (X = r) = C_{r} {(\frac{1}{4})}^{r} {(\frac{3}{4})}^{10 - r} \\ P (X \geq 1) \\ = 1 - P (X < 1) \\ = 1 - P (X = 0) \\ = 1 - C_{0} {(\frac{1}{4})}^{0} {(\frac{3}{4})}^{10} \\ = 0.9437 \end{array}

8.1b Mean, Variance And Standard Deviation Of A Binomial Distribution

Posted on April 23, 2020 by user

8.1b Mean, Variance and Standard Deviation of a Binomial Distribution

2. Determine the mean, variance and standard deviation of binomial distribution.

If X is a binomial discrete random variable such that X ~ B (n, p),

then

Mean of X,

μ = n p

Variance of X,

σ^{2} = n p q

Standard deviation of X,

σ = \sqrt{n p q}

Example 1:

A Football club organises a practice session for trainees on scoring goals from penalty kicks. Each trainee takes 8 penalty kicks. The probability that a trainee scores a goal from a penalty kick is p. After the session, it is found that the mean number of goals for a trainee is 7.2.

Find the value of p.

Solution:

Mean = np

np = 7.2

8p = 7.2

p = 0.9

Example 2:

X is a binomial random variable such that X ~ B (n, p). If its mean and standard deviation are 90 and

3 \sqrt{7}

respectively, find the value of p and of n.

Solution:

\begin{array}{l} Mean = 90 \\ n p = 90 \\ Standard deviation = 3 \sqrt{7} \\ \sqrt{n p q} = 3 \sqrt{7} \\ n p q = 9 (7) \leftarrow Square both sides \\ n p q = 63 \\ (n p) q = 63 \\ 90 q = 63 \\ q = \frac{7}{10} \\ ∴ p = 1 - \frac{7}{10} = \frac{3}{10} \\ From n p = 90, \\ n (\frac{3}{10}) = 90 \\ n = 300 \end{array}