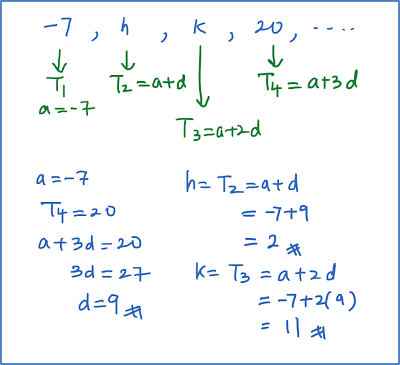
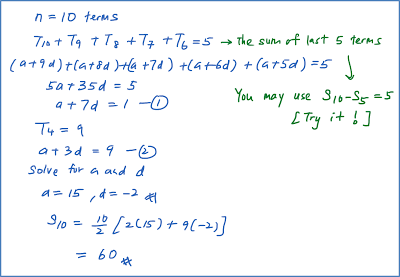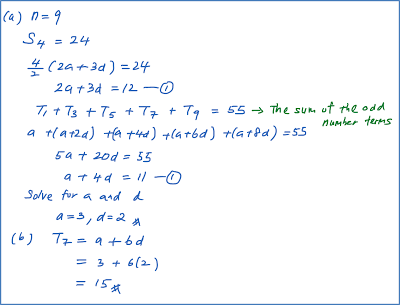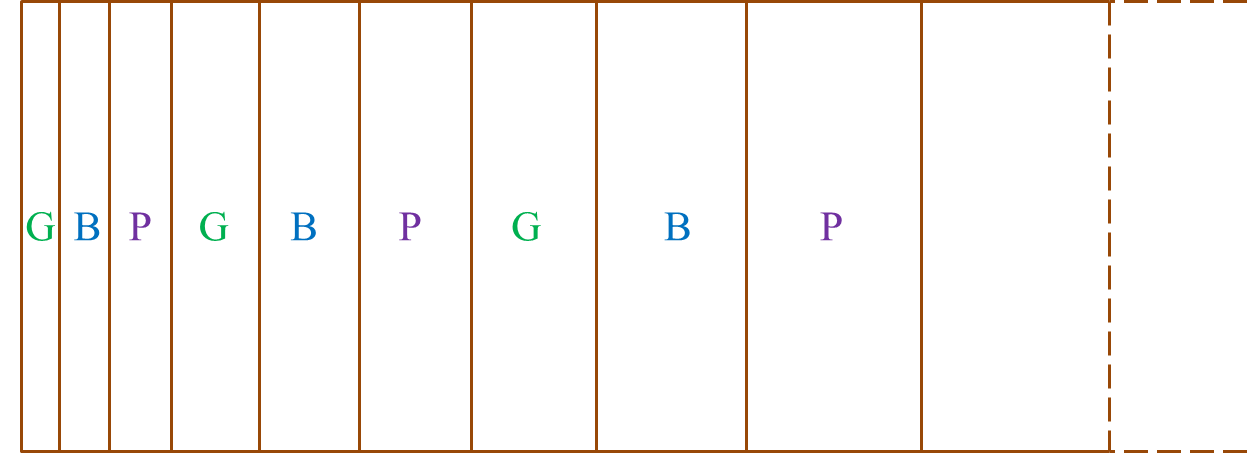Question 2:
The third term and the sixth term of a geometric progression are 24 and 719 respectively. Find
(a) the first term and the common ratio,
(b) the sum of the first five terms,
(c) the sum of the first n terms with n is very big approaching rn ≈ 0.
Solution:
(a)
Given T3=24 ar2=24 ...........(1)Given T6=719 ar5=649 ...........(2)(2)(1):ar5ar2=64924 r3=827 r=23
Substitute r=23 into (1) a(23)2=24a(49)=24 a=24×94 =54∴ the first term 54 and the common ratio is 23.
(b)
S5=54[1−(23)5]1−23 =54×211243×31 =14023∴ sum of the first five term is 14023.
(c)
When −1<r<1 and n becomes very big approaching rn≈0,∴ Sn=a1−r =54 1 − 23 =162
Therefore, sum of the first n terms with n is very big approaching rn ≈ 0 is 162.
The third term and the sixth term of a geometric progression are 24 and 719 respectively. Find
(a) the first term and the common ratio,
(b) the sum of the first five terms,
(c) the sum of the first n terms with n is very big approaching rn ≈ 0.
Solution:
(a)
Given T3=24 ar2=24 ...........(1)Given T6=719 ar5=649 ...........(2)(2)(1):ar5ar2=64924 r3=827 r=23
Substitute r=23 into (1) a(23)2=24a(49)=24 a=24×94 =54∴ the first term 54 and the common ratio is 23.
(b)
S5=54[1−(23)5]1−23 =54×211243×31 =14023∴ sum of the first five term is 14023.
(c)
When −1<r<1 and n becomes very big approaching rn≈0,∴ Sn=a1−r =54 1 − 23 =162
Therefore, sum of the first n terms with n is very big approaching rn ≈ 0 is 162.