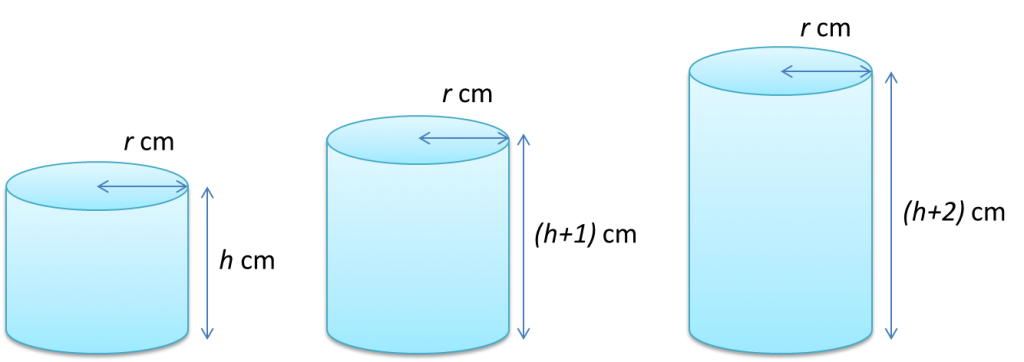
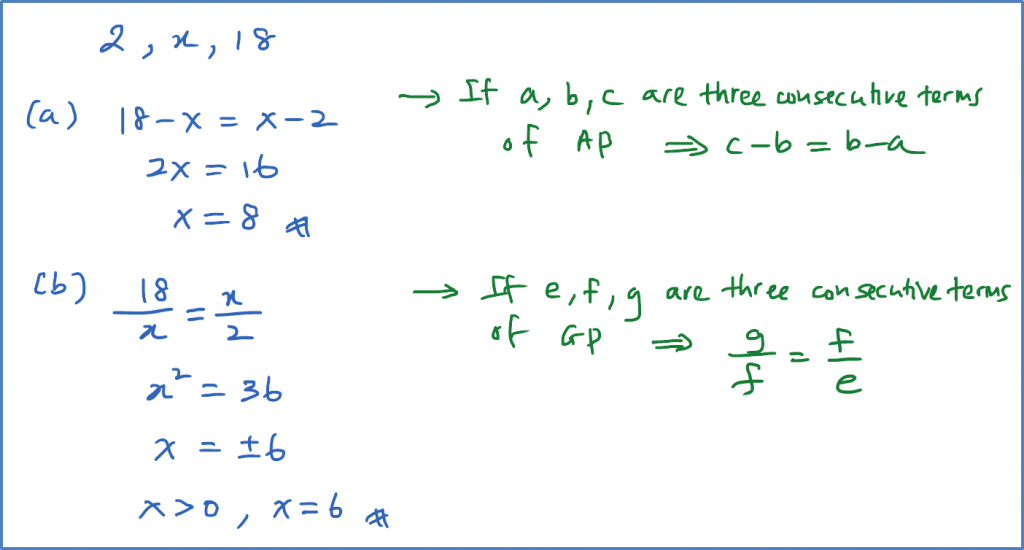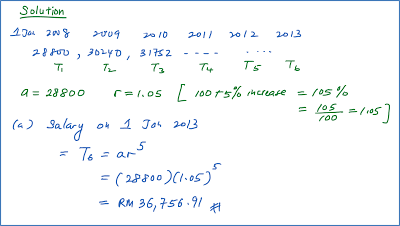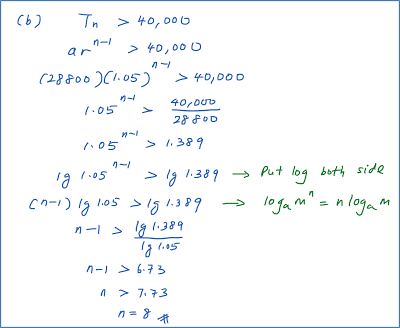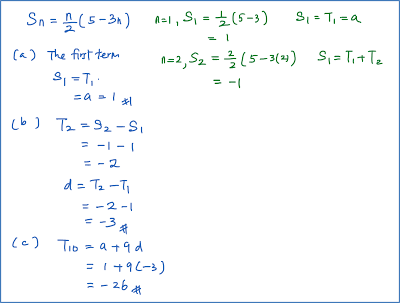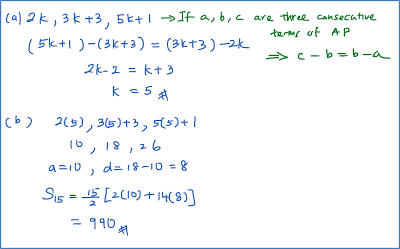Question 4:
The sum of the first n terms of the geometric progression 5, 15, 75, … is 5465.
Find the value of n.
Solution:
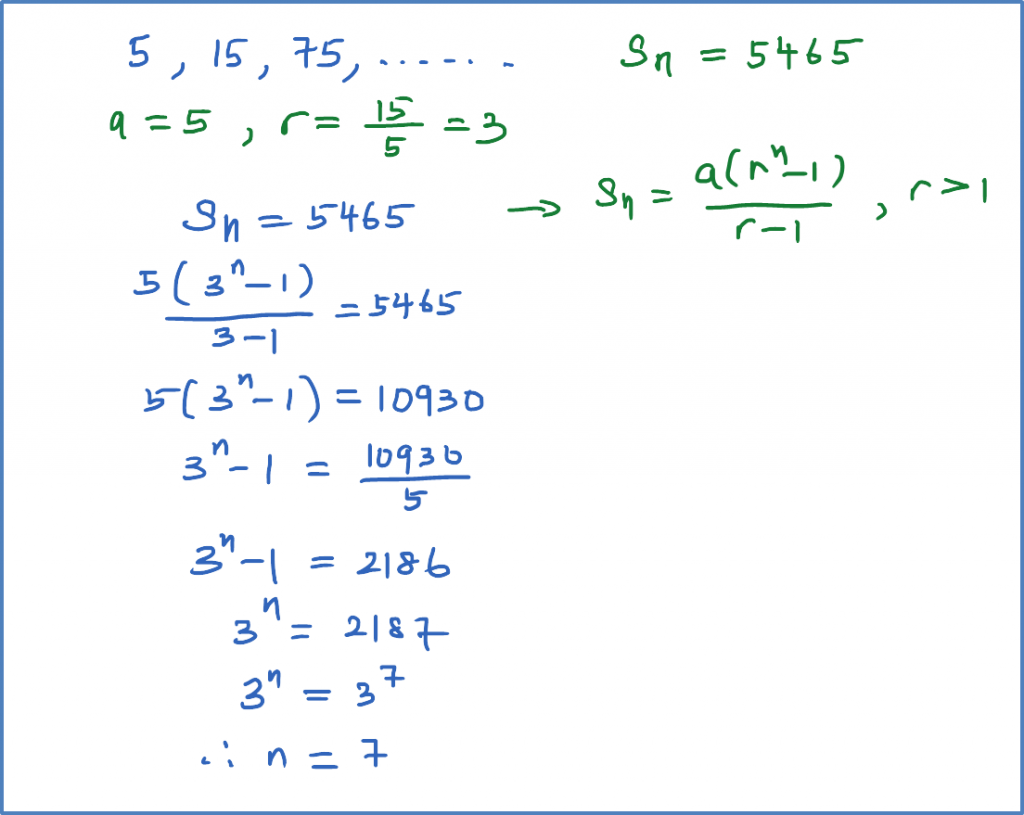
The sum of the first n terms of the geometric progression 5, 15, 75, … is 5465.
Find the value of n.
Solution:
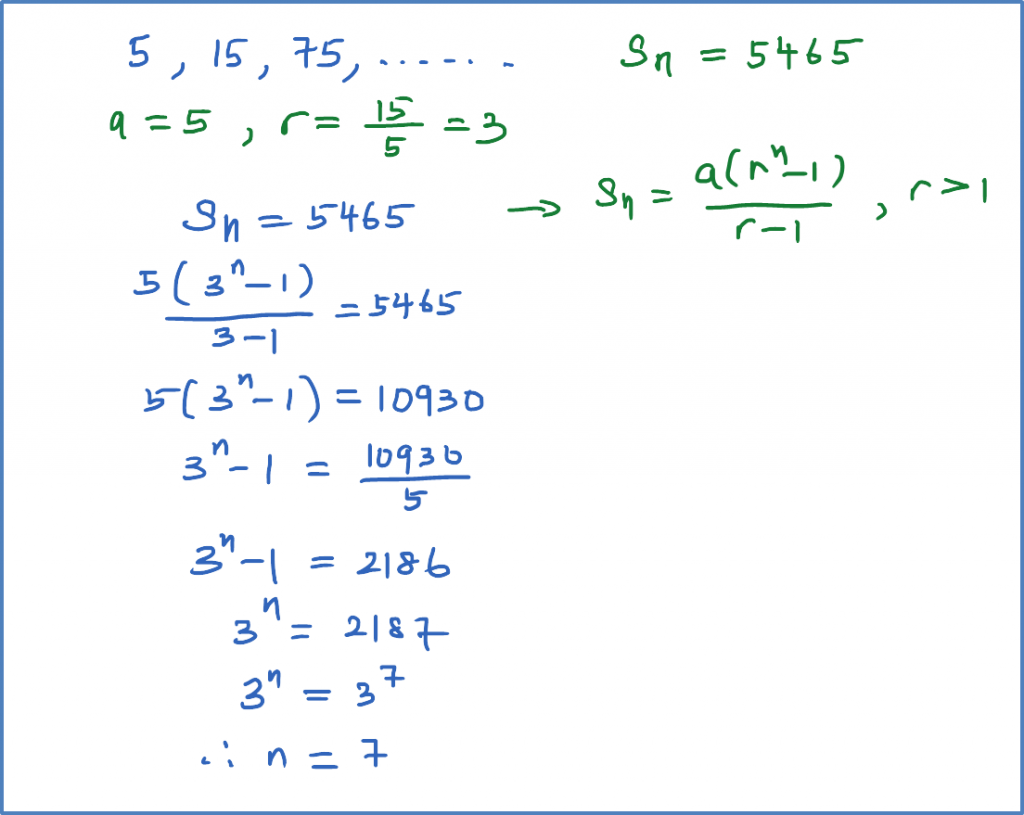
Question 5:
The first three terms of a geometric progression are 5k + 6, 2k, k – 2.
Find
(a) the positive value of k,
(b) the sum from the third term to the sixth term, using the value of k obtained in (a)
Solution:

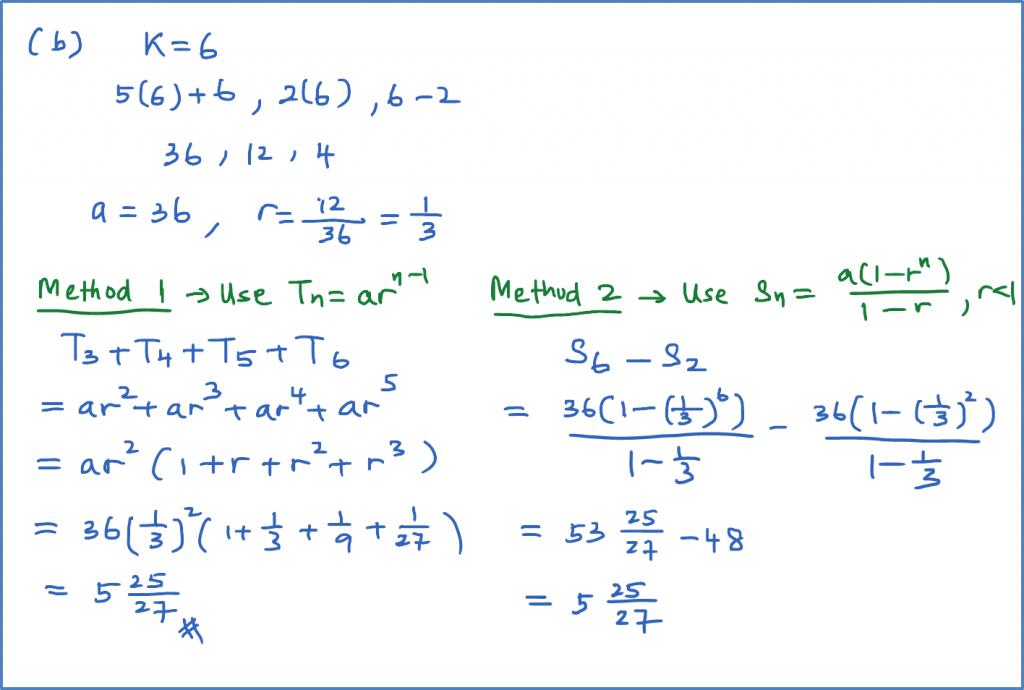
The first three terms of a geometric progression are 5k + 6, 2k, k – 2.
Find
(a) the positive value of k,
(b) the sum from the third term to the sixth term, using the value of k obtained in (a)
Solution:

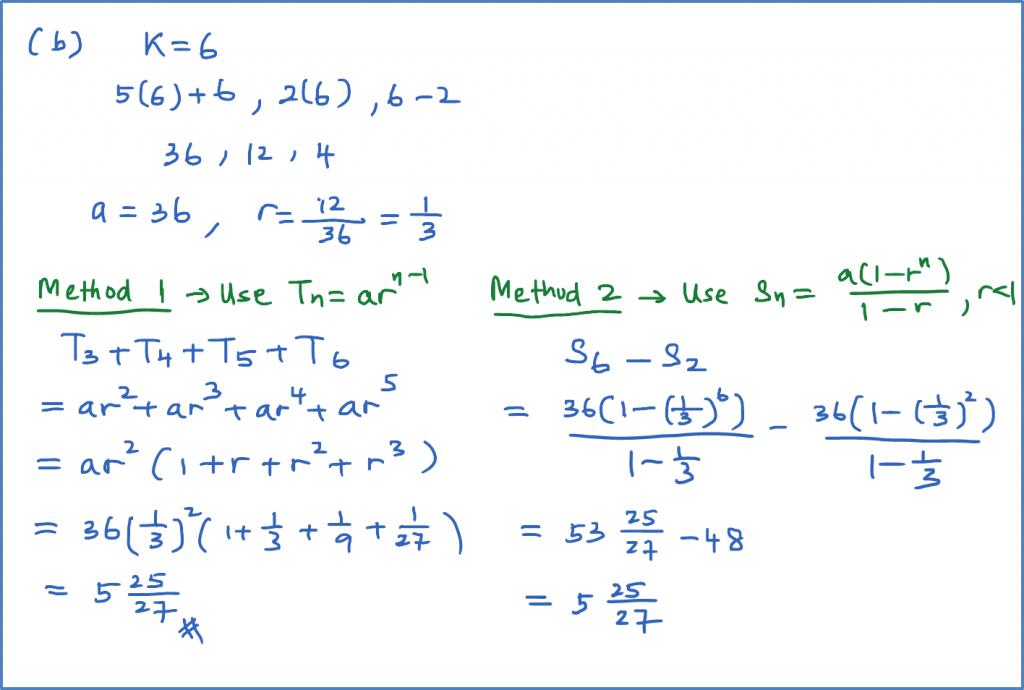
Question 6:
The first three terms of a sequence are 2, x, 18. Find the positive value of x so that the sequence is
(a) an arithmetic progression,
(b) a geometric progression.
Solution:
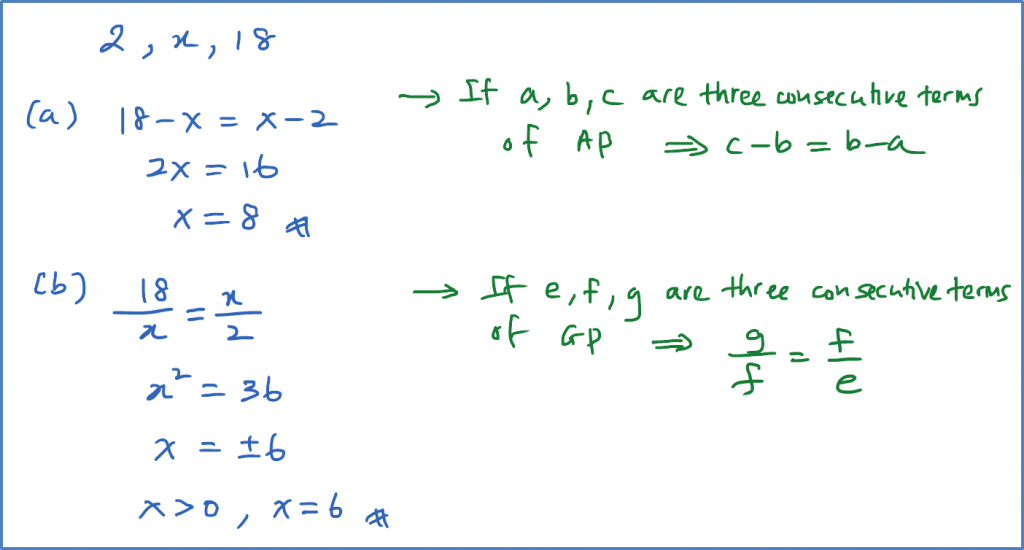
The first three terms of a sequence are 2, x, 18. Find the positive value of x so that the sequence is
(a) an arithmetic progression,
(b) a geometric progression.
Solution: