Question 11 (10 marks):
Solution by scale drawing is not accepted.
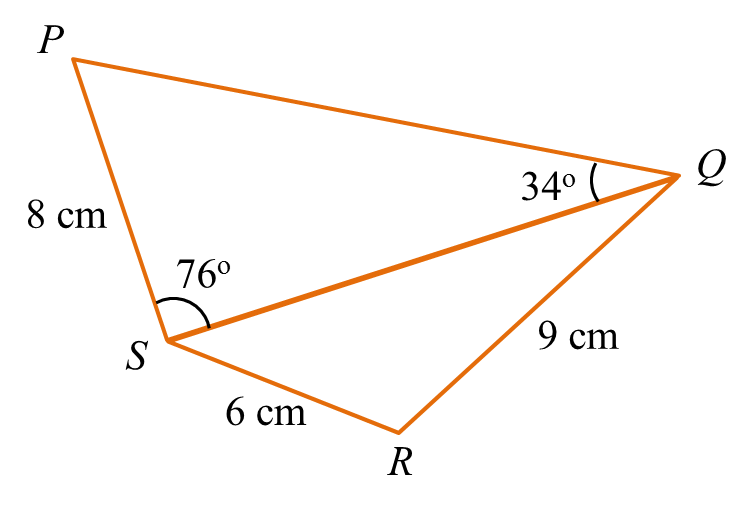
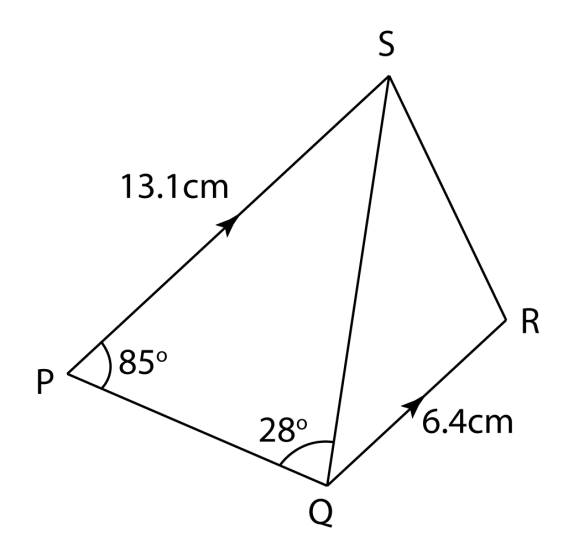
Diagram shows a quadrilateral PQRS on a horizontal plane.
VQSP is a pyramid such that PQ = 12 m and V is 5 m vertically above P.
Find
(a) ∠QSR,
(b) the length, in m, of QS,
(c) the area, in m², of inclined plane QVS.


Solution: 
(a)
$\begin{array}{l}\frac{\sin \angle QSR}{20.5}=\frac{\sin {64}^o}{22}\\ \sin \angle QSR=\frac{\sin {64}^o}{22}\times 20.5\\ \sin \angle QSR=0.8375\\ \angle QSR={56}^{o}52\text{'}\end{array}$


(b)
$\begin{array}{l}\angle QRS={180}^o-{64}^o-{56}^{o}52\text{'}\\ ={59}^{o}8\text{'}\\ \frac{QS}{\sin {59}^{o}8\text{'}}=\frac{22}{\sin {64}^o}\\ QS=\frac{22}{\sin {64}^o}\times \sin {59}^{o}8\text{'}\\ QS=21.01\text{ m}\end{array}$


(c)


$\begin{array}{l}Q{V}^2=P{Q}^2+V{P}^2\\ QV=\sqrt{{12}^2+5^2}\\ QV=13\text{ m}\\ \\ S{V}^2=P{S}^2+V{P}^2\\ SV=\sqrt{{10}^2+5^2}\\ SV=\sqrt{125}\text{ m}\\ \\ QS=21.01\text{ m}\\ \\ {21.01}^2={13}^2+{\left(\sqrt{125}\right)}^2-2\left(13\right)\left(\sqrt{125}\right)\cos \theta \\ 26\left(\sqrt{125}\right)\cos \theta =169+125-441.42\\ \cos \theta =\frac{169+125-441.42}{26\left(\sqrt{125}\right)}\\ \cos \theta =-0.5071\\ \theta ={120}^{o}28\text{'}\\ \\ \text{Area of }QVS\\ =\frac{1}{2}\times 13\times \sqrt{125}\times \sin {120}^{o}28\text{'}\\ =62.64{\text{ m}}^2\end{array}$

Question 9 (10 marks):
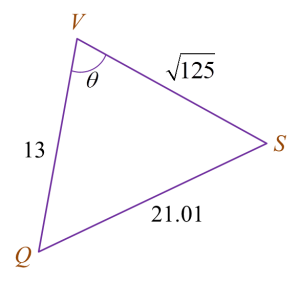
Solution by scale drawing is not accepted.
Diagram shows a transparent prism with a rectangular base PQRS. The inclined surface PQUT is a square with sides 12 cm and the inclined surface RSTU is a rectangle. PTS is a uniform cross section of the prism. QST is a green coloured plane in the prism.


It is given that ∠PST = 37^o and ∠TPS = 45^o.
Find
(a) the length, in cm, of ST,
(b) the area, in cm², of the green coloured plane.
(c) the shortest length, in cm, from point T to the straight line QS.


Solution:
(a)



$\begin{array}{l}\frac{ST}{\sin {45}^o}=\frac{12}{\sin {37}^o}\\ ST=\frac{12}{\sin {37}^o}\times \sin {45}^o\\ ST=14.1\text{ cm}\end{array}$


(b)
$\begin{array}{l}Q{T}^2=Q{P}^2+P{T}^2\\ Q{T}^2={12}^2+{12}^2\\ QT=\sqrt{{12}^2+{12}^2}=16.97\text{ cm}\\ \\ \angle PTS={180}^o-{45}^o-{37}^o={98}^o\\ \\ \frac{PS}{\sin {98}^o}=\frac{12}{\sin {37}^o}\\ PS=\frac{12}{\sin {37}^o}\times \sin {98}^o\\ PS=19.75\text{ cm}\\ \\ Q{S}^2=Q{P}^2+P{S}^2\\ QS=\sqrt{Q{P}^2+P{S}^2}\\ QS=\sqrt{{12}^2+{19.75}^2}\\ QS=23.11\text{ cm}\end{array}$




$\begin{array}{l}Q{S}^2=Q{T}^2+S{T}^2-2\left(QT\right)\left(ST\right)\cos \angle QTS\\ {23.11}^2={16.97}^2+{14.1}^2-2\left(16.97\right)\left(14.1\right)\cos \angle QTS\\ \cos \angle QTS=\frac{{16.97}^2+{14.1}^2-{23.11}^2}{2\left(16.97\right)\left(14.1\right)}\\ \cos \angle QTS=-\frac{47.28}{478.55}\\ \angle QTS={95.67}^o\\ \\ \text{Thus, area of green coloured plane }QTS\\ =\frac{1}{2}\left(16.97\right)\left(14.1\right)\sin {95.67}^o\\ =119.05{\text{ cm}}^2\end{array}$


(c)



$\begin{array}{l}\text{Let the shortest length from point }T\\ \text{to the straight line }QS\text{ is }h.\\ \\ \text{Area of }\Delta QTS=119.05\\ \frac{1}{2}\left(h\right)\left(23.11\right)=119.05\\ h=10.3\text{ cm}\end{array}$

Question 8:
Diagram below shows a cyclic quadrilateral PQRS.


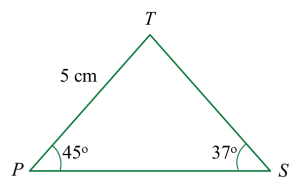
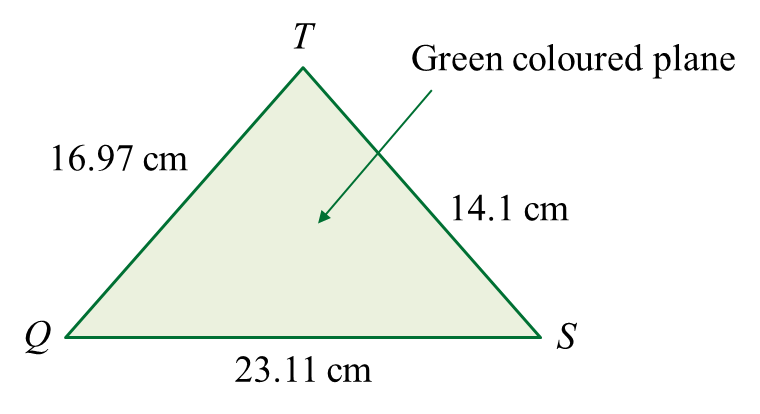
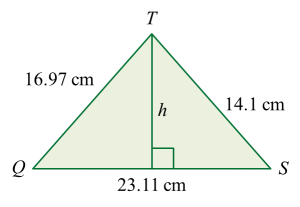
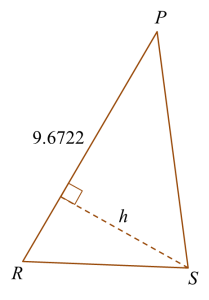
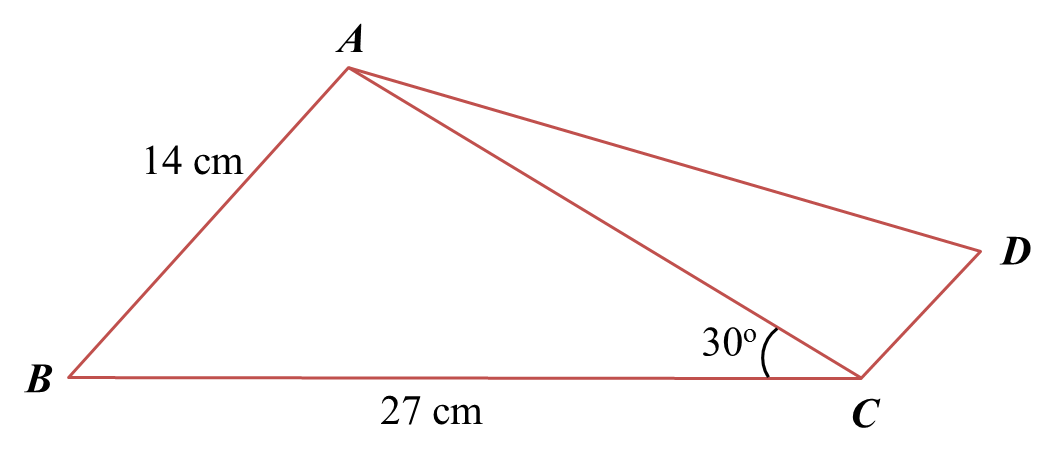
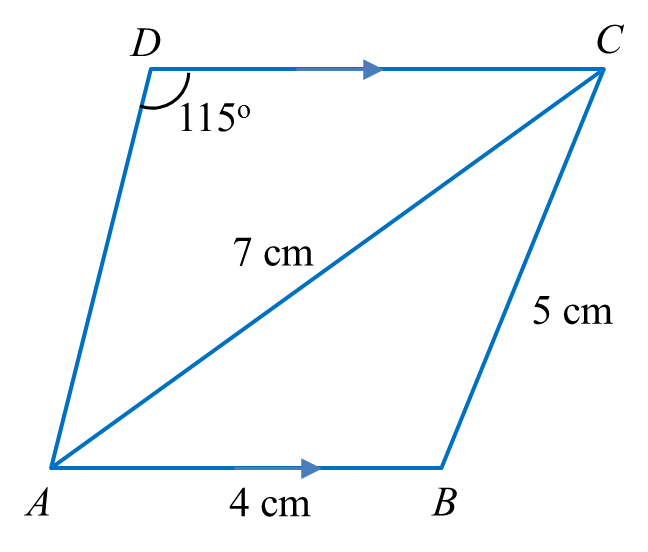(a) Calculate
(i) the length, in cm, of PR,
(ii) ∠PRQ.
(b) Find
(i) the area, in cm², of ∆ PRS,
(ii) the short distance, in cm, from point S to PR.

Solution:
(a)(i)
$\begin{array}{l}P{R}^2=7^2+8^2-2\left(7\right)\left(8\right)\cos {80}^o\\ P{R}^2=113-19.4486\\ PR=\sqrt{93.5514}\\ PR=9.6722\text{ cm}\end{array}$


(a)(ii)
$\begin{array}{l}\text{In cyclic quadrilateral}\\ \angle PQR+\angle PSR=180\\ \angle PQR+80=180\\ \angle PQR={100}^o\\ \\ \frac{\sin \angle QPR}{3}=\frac{\sin 100}{9.6722}\\ \sin \angle QPR=0.3055\\ \angle QPR={17}^{o}47\text{'}\\ \\ \angle PRQ={180}^o-{100}^o-{17}^{o}47\text{'}\\ ={62}^{o}13\text{'}\end{array}$


(b)(i)
$\begin{array}{l}\text{Area of }△PRS\\ =\frac{1}{2}\times 7\times 8\sin {80}^o\\ =27.5746{\text{ cm}}^2\end{array}$


(b)(ii)


$\begin{array}{l}\text{Area of }△PRS=27.5746\\ \frac{1}{2}\times 9.6722\times h=27.5746\\ h=\frac{27.5746\times 2}{9.6722}\\ =5.7018\text{ cm}\\ \text{Shortest distance}=5.7018\text{ cm}\end{array}$

Question 7:
Diagram below shows a quadrilateral ABCD where the sides AB and CD are parallel. ∠BAC is an obtuse angle.

Given that AB = 14 cm, BC = 27 cm, ∠ACB = 30^o and AB : DC = 7 : 3.
Calculate
(a) ∠BAC.
(b) the length, in cm, of diagonal BD.
(c) the area, in cm², of quadrilateral ABCD.

Solution:
(a)
$\begin{array}{l}\frac{\sin \angle BAC}{27}=\frac{\sin {30}^o}{14}\\ \sin \angle BAC=\frac{\sin {30}^o}{14}\times 27\\ \sin \angle BAC=0.9643\\ \angle BAC={74.64}^o\\ \angle BAC\left(\text{obtuse}\right)={180}^o-{74.64}^o\\ ={105.36}^o\end{array}$


(b)
$\begin{array}{l}AB\text{ parallel with }DC\\ \angle BAC=\angle ACD\\ \angle BCD={105.36}^o+{30}^o\\ ={135.36}^o\\ \frac{DC}{AB}=\frac{3}{7}\\ DC=\frac{3}{7}\times 14\text{ cm}\\ =6\text{ cm}\\ \\ B{D}^2={27}^2+6^2-2\left(27\right)\left(6\right)\cos \angle BCD\\ B{D}^2=765-324\cos {135.36}^o\\ B{D}^2=995.54\\ BD=31.55\text{ cm}\end{array}$


(c)
$\begin{array}{l}\angle ABC={180}^o-{30}^o-{105.36}^o\\ ={44.64}^o\\ \\ A{C}^2={27}^2+{14}^2-2\left(27\right)\left(14\right)\cos \angle ABC\\ A{C}^2=925-756\cos {44.64}^o\\ A{C}^2=387.08\\ AC=19.67\text{ cm}\\ \\ \text{Area }△ABC\\ =\frac{1}{2}\left(14\right)\left(27\right)\sin {44.64}^o\\ =132.80{\text{ cm}}^2\\ \\ \text{Area }△ACD\\ =\frac{1}{2}\left(19.67\right)\left(6\right)\sin {105.36}^o\\ =56.90{\text{ cm}}^2\\ \\ \text{Area of quadrilateral }ABCD\\ =132.80+56.90\\ =189.7{\text{ cm}}^2\end{array}$