10.3 Area of Triangle

Posted on April 22, 2020 by user

10.3 Area of Triangle

Example:

Calculate the area of the triangle above.

Solution:

$\begin{array}{l} A r e a = \frac{1}{2} a b \sin C \\ A r e a = \frac{1}{2} (7) (4) \sin 40^{o} \\ A r e a = 9 {cm}^{2} \end{array}$

Example:

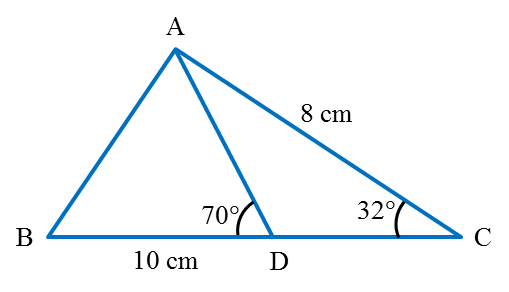
Diagram above shows a triangle ABC, where AC = 8 cm and ∠C = 32^o. Point D lies on straight line BC where BD = 10 cm and ∠ADB = 70^o . Calculate
(a) the length, in cm, of CD,
(b) the area, in cm² of ∆ ADC,
(c) the area, in cm² of ∆ ABC,
(d) the length, in cm, of AB.

Solution:
(a)

$\begin{array}{l} ∠ A D C + 70^{o} = 180^{o} \\ ∠ A D C = 110^{o} \\ ∠ C A D = 180^{o} - 110^{o} - 32^{o} \\ ∠ C A D = 38^{o} \\ Using Sine Rule, \\ \frac{8}{\sin 110^{o}} = \frac{C D}{\sin 38^{o}} \\ C D \sin 110^{o} = 8 \sin 38^{o} \\ C D (0.940) = 8 (0.616) \\ C D = 5.243 \end{array}$

(b)

$\begin{array}{l} Area of △ A D C \\ = \frac{1}{2} (8) (5.243) sin 32^{o} \\ = 20.972 (0.530) \\ = 11.12 {cm}^{2} \end{array}$

(c)

$\begin{array}{l} Area of △ A B C \\ = \frac{1}{2} (8) (10 + 5.243) sin 32^{o} \\ = 60.972 (0.530) \\ = 32.315 {cm}^{2} \end{array}$

(d)

$\begin{array}{l} Use Cosine Rule for △ A B C, \\ A B^{2} = {15.243}^{2} + 8^{2} - 2 (15.243) (8) \cos 32^{o} \\ A B^{2} = 232.35 + 64 - 206.83 \\ A B^{2} = 89.52 \\ A B = 9.462 cm \end{array}$

10.2 The Cosine Rule

Posted on April 22, 2020 by user

10.2 The Cosine Rule

The cosine rule can be used when

(i) two sides and the included angle, or

(ii) three sides of a triangle are given.

(A) If you know 2 sides and 1 angle between them [included angle] ⇒ Cosine rule

Example:

Calculate the length of AC, x, in cm for the triangle above.

Solution:

$\begin{array}{l} b^{2} = a^{2} + c^{2} - 2 a c \cos B \\ x^{2} = 4^{2} + 7^{2} - 2 (4) (7) \cos 50^{\circ} \\ x^{2} = 16 + 49 - 56 (0.6428) \\ x^{2} = 65 - 35.997 \\ x^{2} = 29.003 \\ x = 5.385 cm \end{array}$

(B) If you know 3 sides ⇒ Cosine rule

Example:

Calculate ÐBAC for the triangle above.

Solution:

$\begin{array}{l} \cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} \\ \cos ∠ B A C = \frac{7^{2} + 6^{2} - 8^{2}}{2 (7) (6)} \\ \cos ∠ B A C = 0.25 \\ ∠ B A C = \cos^{- 1} 0.25 \\ ∠ B A C = {75.52}^{o} \end{array}$

10.1 The Sine Rule

Posted on April 22, 2020 by user

10.1 The Sine Rule

In a triangle ABC in which the sides BC, CA and AB are denoted by a, b, and c as shown, and A, B, C are used to denote the angles at the vertices A, B, C respectively,

The sine rule can be used when

(i) two sides and one non-included angle or

(ii) two angles and one opposite side are given.

(A) If you know 2 angles and 1 side ⇒ Sine rule

Example:

Calculate the length, in cm, of AB.

Solution:

∠ACB = 180^o – (50^o + 70^o) = 60^o

$\begin{array}{l} \frac{A B}{\sin 60^{o}} = \frac{4}{\sin 50^{o}} \\ A B = \frac{4 \times \sin 60^{o}}{\sin 50^{o}} \\ A B = 4.522 cm \end{array}$

(B) If you know 2 sides and 1 angle (but not between them) ⇒ Sine rule

Example:

Calculate ∠ACB.

Solution:

$\begin{array}{l} \frac{28}{\sin 54^{o}} = \frac{26}{\sin ∠ A C B} \\ \sin ∠ A C B = \frac{26 \times \sin 54^{o}}{28} \\ \sin ∠ A C B = 0.7512 \\ ∠ A C B = {48.7}^{o} \end{array}$

(C) Case of ambiguity (2 possible triangles)

Example

Calculate ∠ACB, θ.

Solution:

Two possible triangle with these measurement

AB = 26cm BC = 28 cm Ð BAC = 54^o

$\begin{array}{l} \frac{26}{\sin θ} = \frac{28}{\sin 54^{o}} \\ \sin θ = 0.7512 \\ θ = \sin^{- 1} 0.7512 \\ θ = {48.7}^{o}, 180^{o} - {48.7}^{o} \\ θ = {48.7}^{o} (Acute angle), {131.3}^{o} (Obtuse angle) \end{array}$